Champernowne graphique
(et autres décimalisations)
J’ai envoyé par courrier privé à Jean-Marc Falcoz et Maximilian Hasler l’idée suivante :
> prendre la constante de Champernowne et embarquer pour une promenade en suivant, chiffre à chiffre, ces instructions :
- quand le chiffre est pair (0,2,4,6,8) on effectue un virage de 90° à droite puis on marche tout droit en effectuant respectivement 0, 2, 4, 6 ou 8 pas ;
- quand le chiffre est impair (1,3,5,7,9) on effectue un virage de 90° à gauche puis on marche tout droit en effectuant respectivement 1, 3, 5, 7 ou 9 pas.
Jean-Marc et Maximilian furent intéressés et se mirent à calculer.
Voici, en guise d’exemple, comment aller de 0 à 54, chiffre par chiffre – départ en bas à droite, sur le point vert et arrivée près du bord gauche (illustration de Jean-Marc Falcoz) ; attention, le traitement du zéro est délicat (pour mon premier essai de dessin, je me suis fait reprendre comme un bleu par Jean-Marc et Maximilian) :
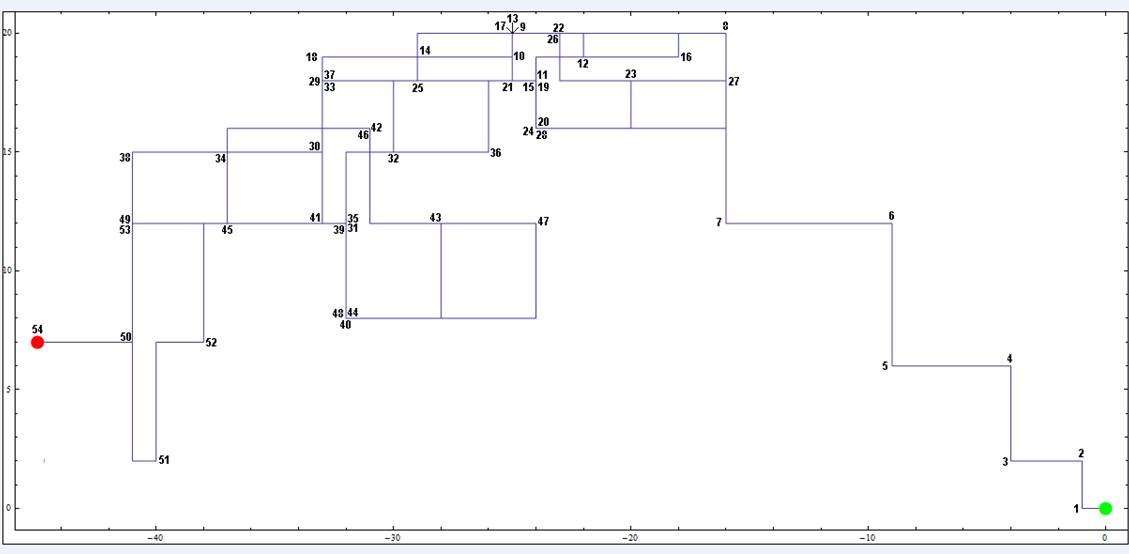
... Voici les 1000 premiers chiffres du nombre de Champernowne, dessinés par Jean-Marc Falcoz (le trajet commence au point vert (0,0) en haut à gauche, monte un tout petit peu, descend, change de cadran une première fois, puis une seconde fois – et finit par s’enfoncer inexorablement le sud-est) :
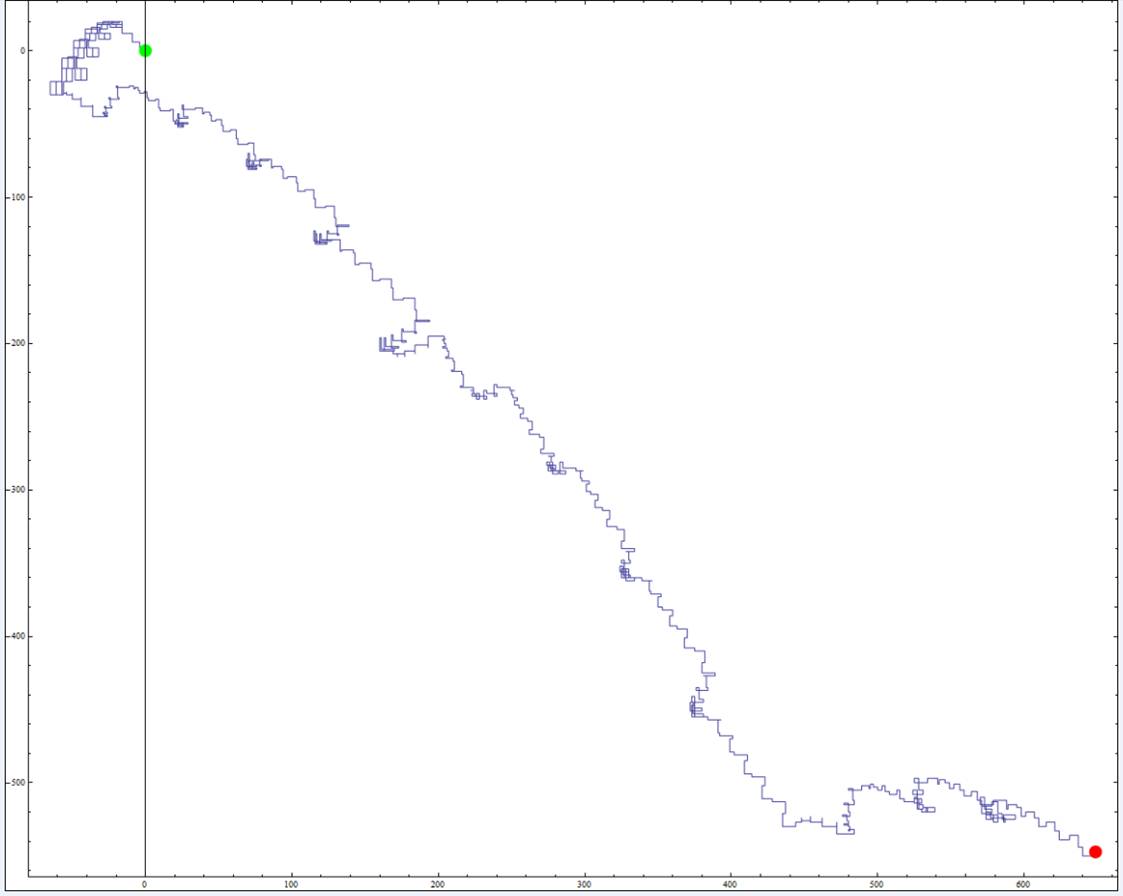
Calcul par Jean-Marc des 1000 premiers entiers concaténés :
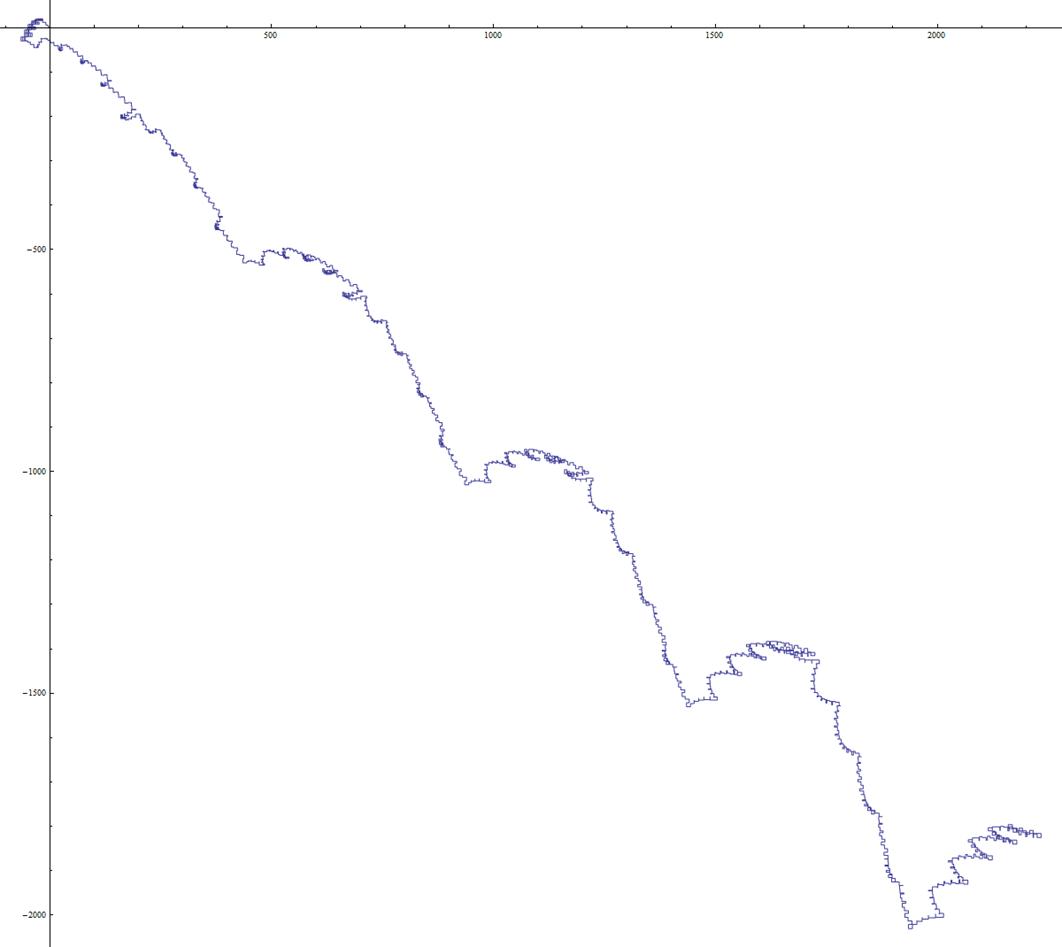
Confirmation de cette trajectoire – calculée indépendamment par Maximilian Hasler :
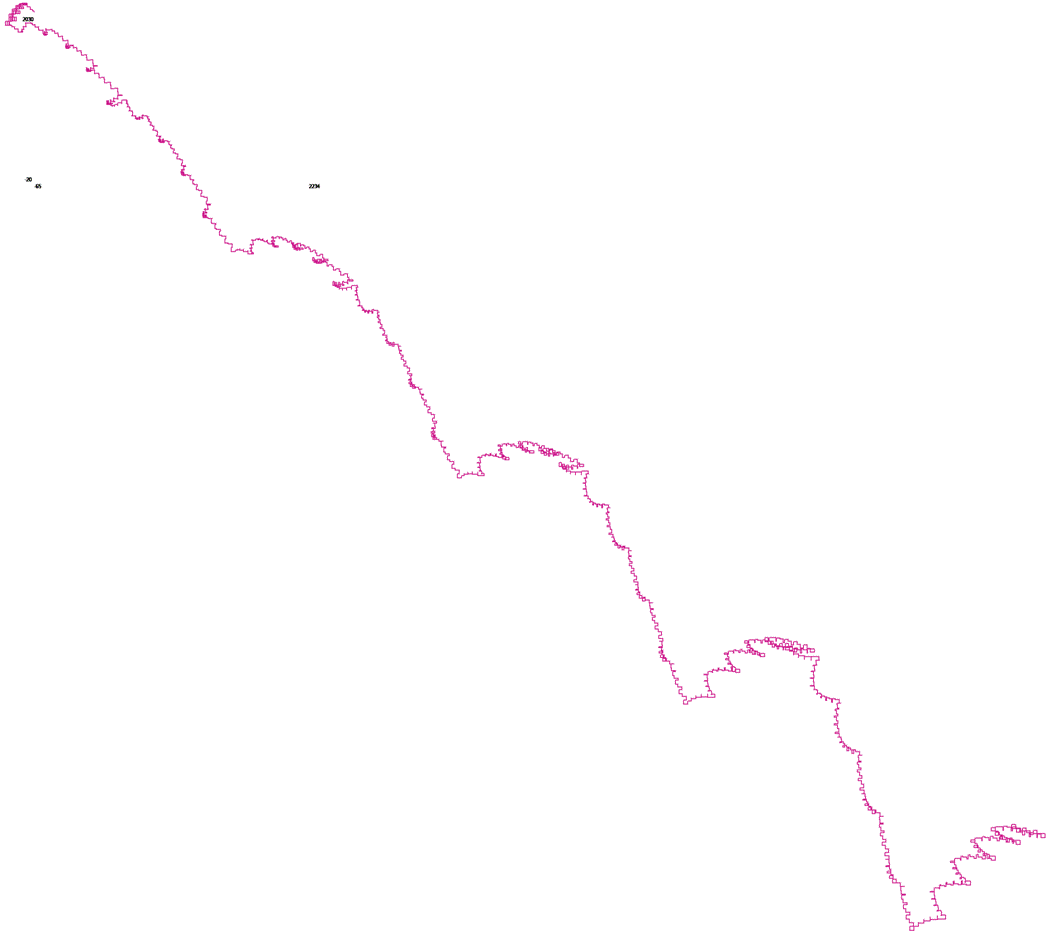
... Ci-dessous, les 10000 premiers chiffres du nombre de Champernowne, dessinés par Jean-Marc :
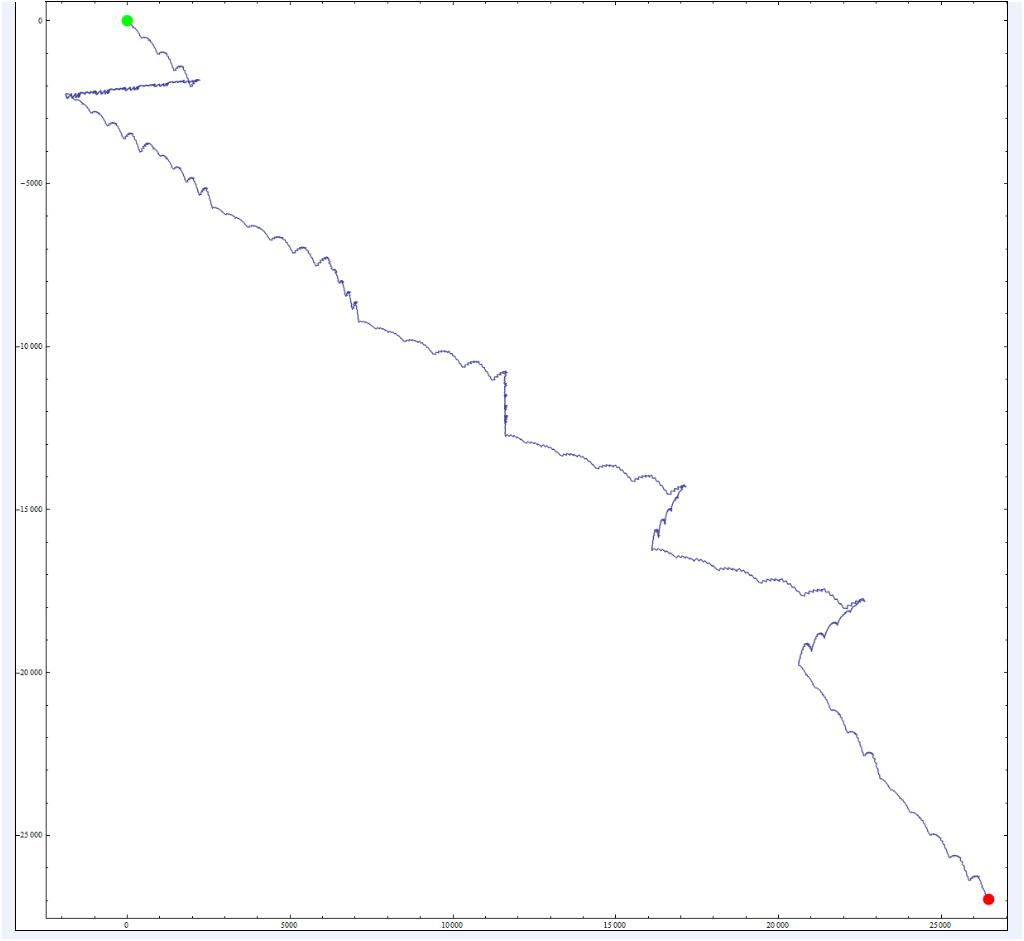
... et les 200000 premiers chiffres du même nombre de Champernowne, toujours par Jean-Marc :
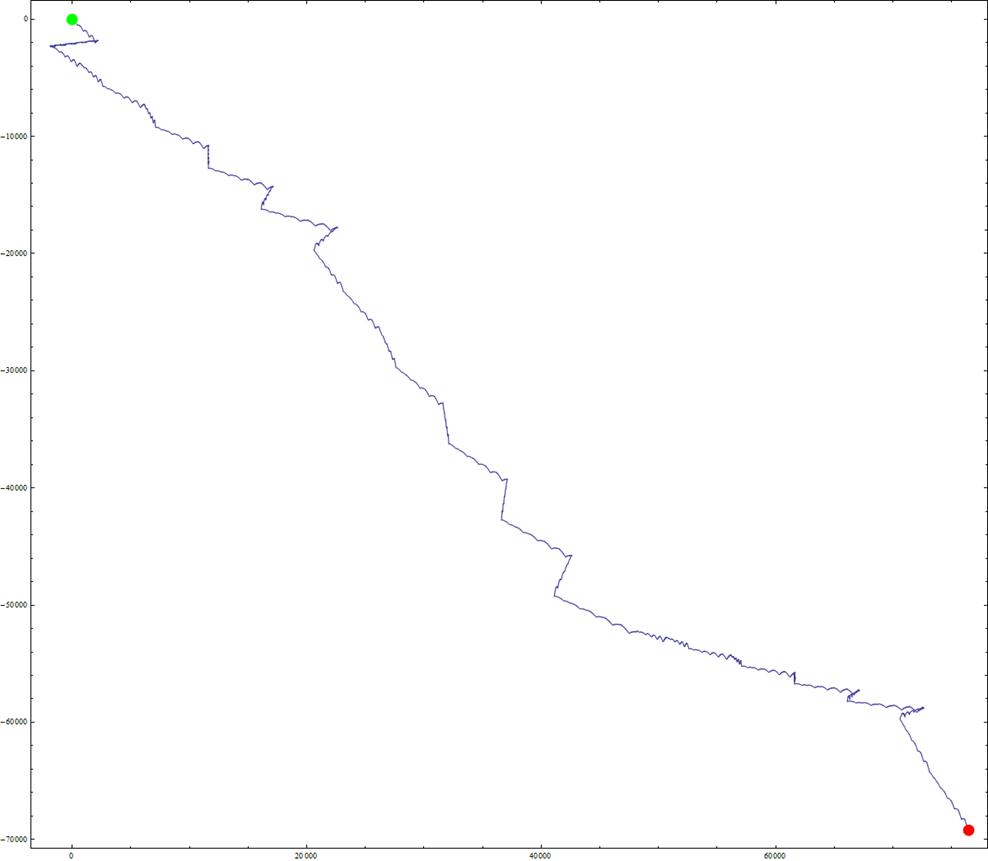
Voici les 100000 premières décimales du nombre « e », allant du point vert au rouge (toujours par Jean-Marc) :
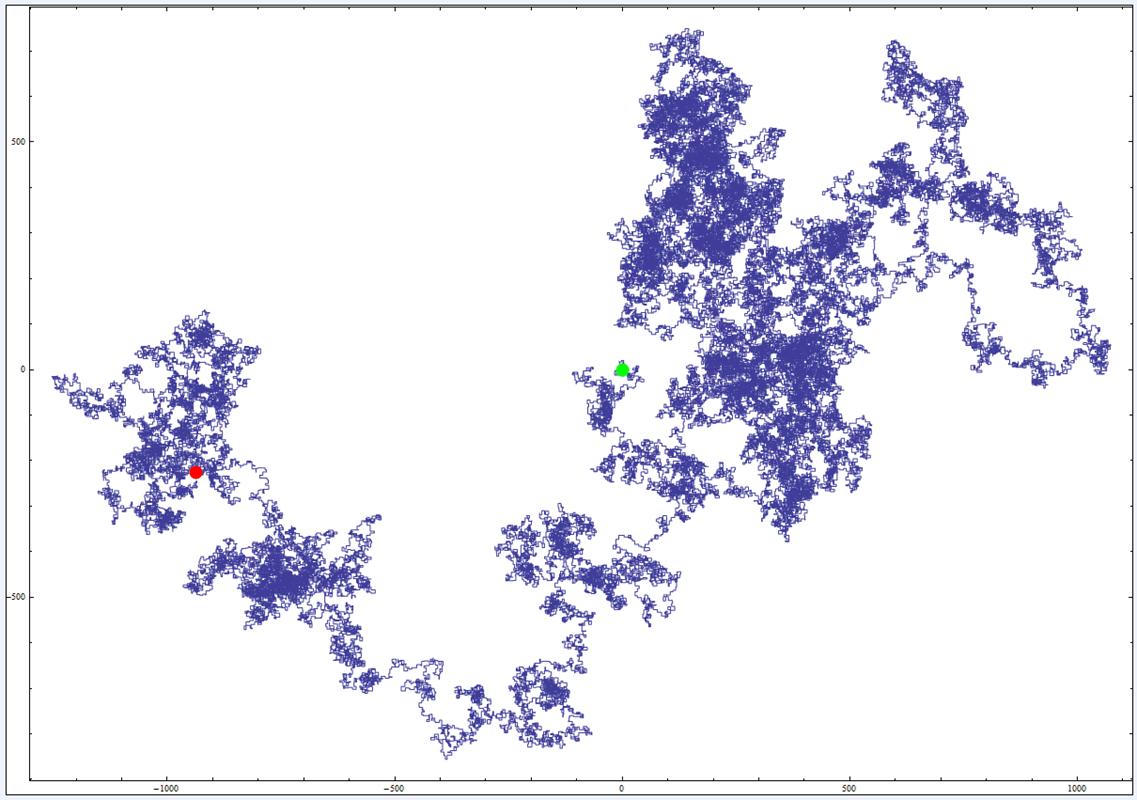
10000 décimales de Pi (du point vert au point sombre, en bas), par Jean-Marc :
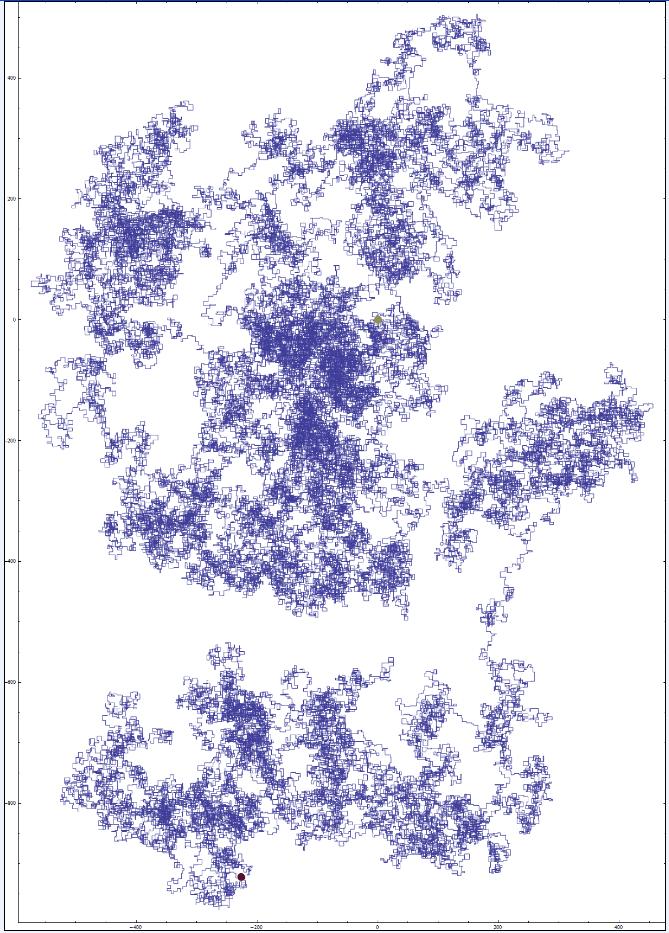
Jean-Marc a eu l’idée de représenter des nombres ayant des décimales qui reviennent périodiquement ;
1/7, par exemple, produit à l’infini le motif « en escalier » suivant :
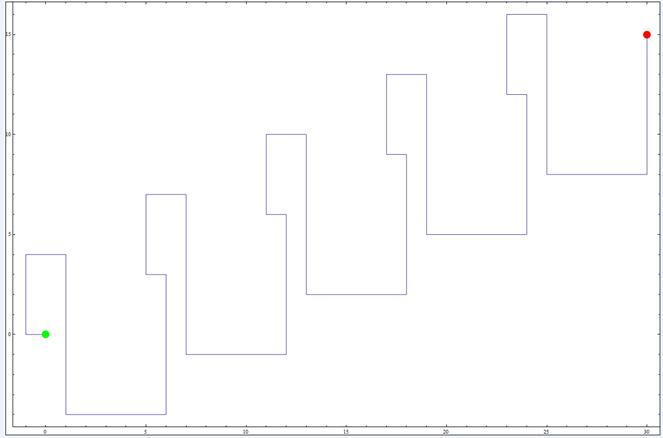
La fraction 1/317 boucle sur elle-même :
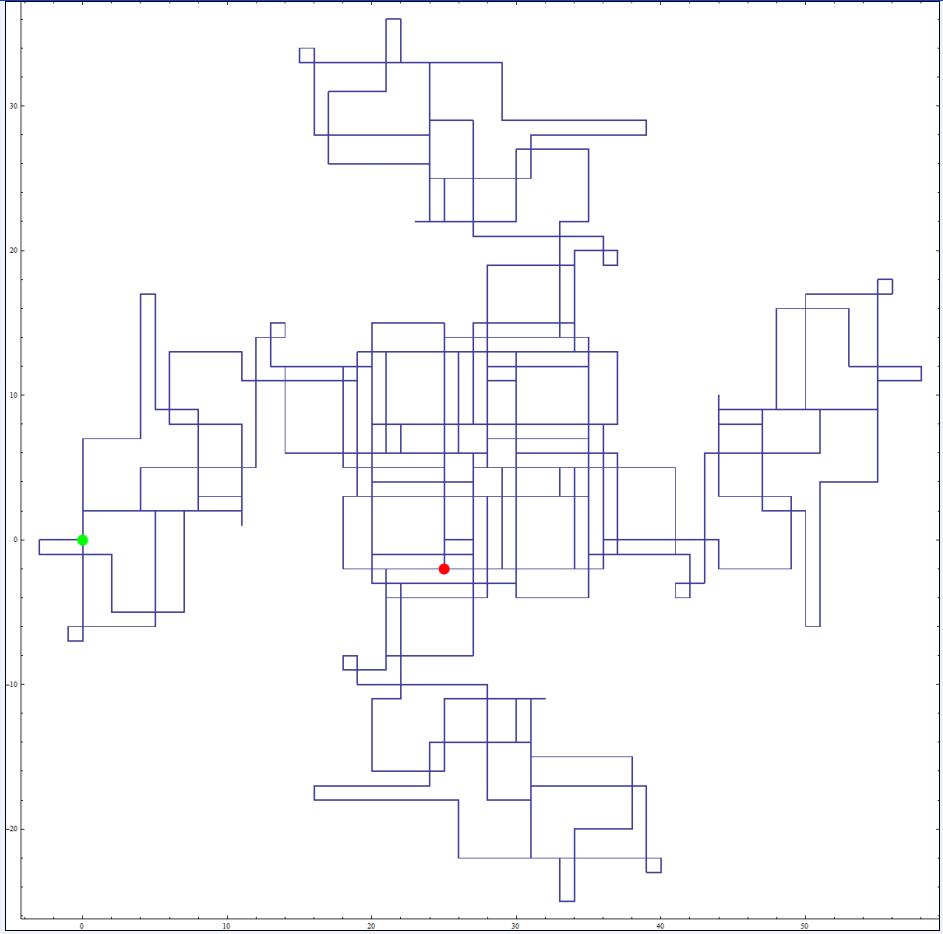
La fraction 1/317317 cascade infiniment vers le sud-est :
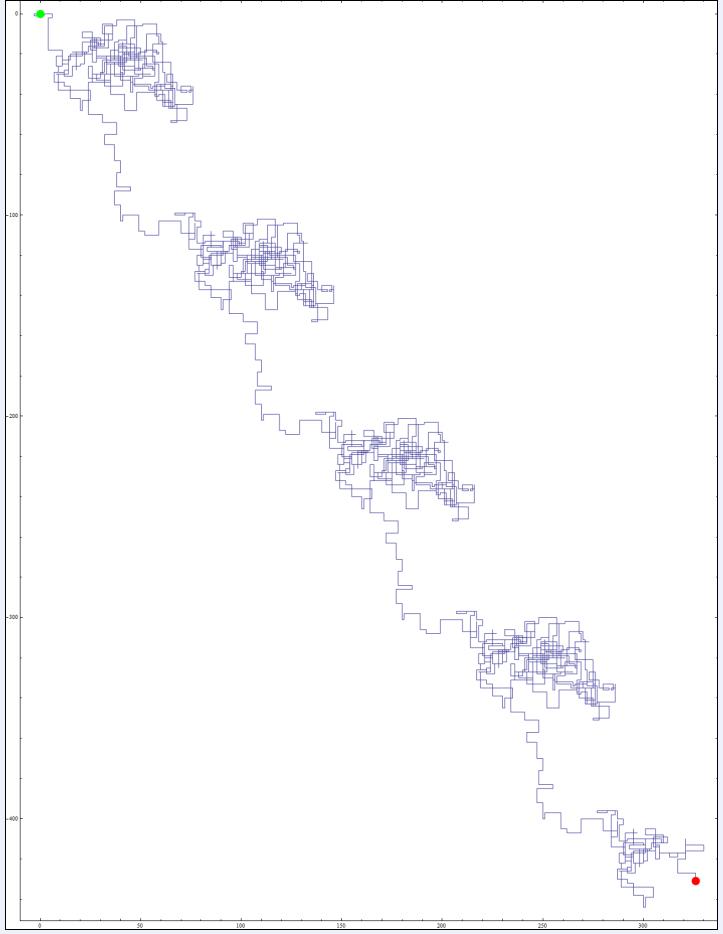
Jean-Marc a plein d’idées encore : qui calculera, par exemple, la suite des entiers tels que 888624355 ? Ils n’ont aucun point par lequel leur trajectoire ne repasse :
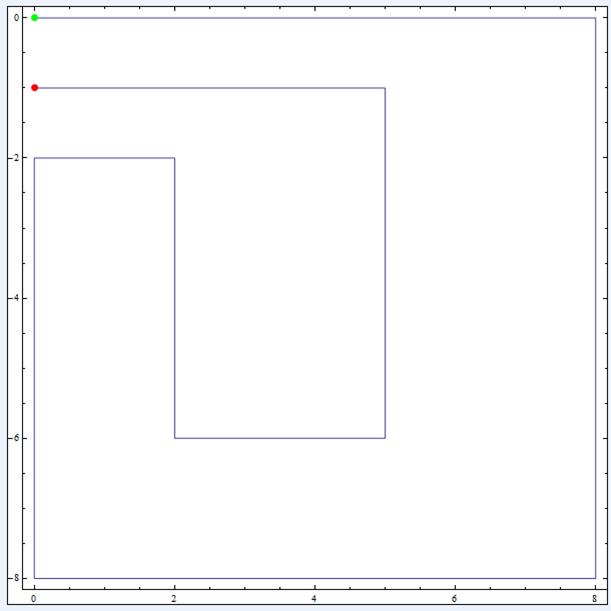
More to come, stay tuned!
__________
A last word (for
today) by Jean-Marc:
Je viens de faire un
programme qui trouve et affiche graphiquement les nombres dont les trajectoires
commencent et finissent en (0,0), ne se croisent pas et ne repassent pas deux
fois par le même point (on fait une exception pour les 0 internes (la
trajectoire d’un nombre contenant par exemple ...807... on pourrait considérer
que la trajectoire passe deux fois par le même point à cause du 0, mais comme
le segment en question a une longueur nulle, je ne considère pas qu’elle
repasse deux fois par ce point) :
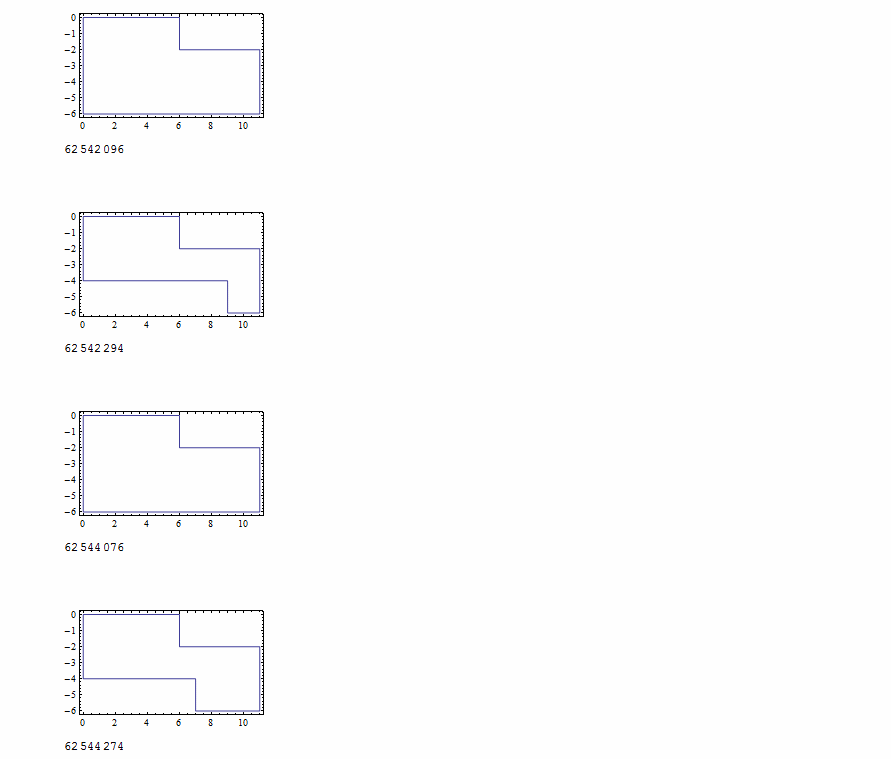
__________
[Breaking news]:
Voici le message posté ce matin par Maximilian à la liste SeqFans:
Dear
SeqFans,
inspired by a private communication
from Eric Angelini,
I
suggest a new(?) [integer]
sequence transformations
(plus some variants), which I tentatively call "Turtle
transformation"(s)
(in memoriam of the turtle graphics in the Logo programming
language)
The
complex Turtle transformation of a sequence
a : n -> a(n) , n >= offset ;
is the sequence obtained from a(n) by
1) defining a sequence of "directions"
d(n) = d(n-1) * i * (-1)^a(n) ;
d(offset-1)=1
2) then the Turtle transform is the sequence of partial sums of
"steps
of length" a(n) "in
direction" d(n), i.e., d(n)*a(n),
T(a) = n -> sum_{k=offset...n}
d(k)*a(k) ; T(a)(offset-1) = 0.
The
interpretation is that T(a) represents a
"walk" in the complex plane,
where at the n-th
step, the "cursor" turns to the left or to the right
depending on the parity of a(n), and
then walks a distance of a(n)
units.
This
in turn gives rise to at least 3 (integer) sequences (if a(n)
is
an integer sequence), namely
Re T(a) ; Im T(a) ; and
S(a) = these two interleaved, i.e.
S(a)(2n-1)=Re
T(a)(n) ; S(a)(2n)=Im T(a)(n).
There
are several variants possible:
a) use abs( a(n) ) instead of a(n) in case of a signed sequence
(this will destroy bijectivity)
b) don’t use only left or right turns depending on parity, but
rather
a
turn of 90° * a(n).
c) use a second sequence, b(n), for the "turns", to
define the
b-Turtle
transform of a(), say T[b](a) or T(a ; b) = sum( d[b](k) *
a(k), k=offset..n
)
with
d[b](n) = product( i^b(k) ; k=offset...n
) [or prod( i * (-1)^b(k)...) ]
d) use some other initial condition for the direction (a priori
just
amounts to a multiplication by a unimodular number of the transformed
sequence)
or, e.g., the opposite convention for
turning left or right (which
should correspond to a change of sign and/or
complex conjugation).
It
is easy to see that both, the b-Turtle and (a-)Turtle
transformation, are bijective.
For
sequences with only odd numbers, such as the primes, the variant
(b) above is more "interesting". I will denote it by
T’, and look at
its action on prime=A40:
It
turns out that T’(prime)(56) = -13+8*i, i.e., almost
exactly back
to the origin, after having made an
"excursion" as far as 702 - 1197*i
around n=46 ;
then again the cursor goes away to
T’(prime)(78) = -2922 - 1733*i,
before "crossing" the origin during
the 99-th step,
going from -256 + 37*i to 267 + 37*i.
Just
for the fun, I submitted that sequence as oeis.org/draft/A233399
,
including the picture after step 99 (drawn in red),
https://oeis.org/A233399/a233399_1.png
Maximilian
__________
La réponse à Maximilian
par William Keith :
>
I did something like this for primes, although the rule was simply to make
a left turn at node n of the walk if n
was a prime. The results, turned to
graphics using Mathematica,
can be found at
http://earl.of.sandwich.net/Photos/Images/PrimeWalks/
With
sufficient magnification you can see where the 1 is, since it's the
only short end. For example, in
PrimeWalk3080(1899x1173).jpg it is on the
left.
William
Keith
(...or, upon second glance, I think I turned right.)
__________
Illustrations (c) Jean-Marc Falcoz & Maximilian Hasler
[9 décembre 2013]