Colorless green ideas
(I hope this is not old hat)
Let N be an integer
Let S be the sum of N’s digits
--> make M=N+S if S is even
--> make M=N-S if S is odd
Iterate.
Example:
71(+8)=79
79(+16)=95
95(+14)=109
109(+10)=119
119(-11)=108
108(-9)=99
99(+18)=117
117(-9)=108
Thus 71 enters in the loop 99.117.108.99
---
Here is the fate of the first 245
integers below (computed by hand);
- colorless
integers end on zero;
- yellow
integers are attracted in the loop 99.117.108.99;
- grey integers
are attracted in the loop 198.216.207.198:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,
13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32,
33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52,
53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191,
192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 243, 245, ...
---
The next attractor is 297.315.306.297,
I guess (considering the arising pattern). Will there be a change in the
attractor’s behaviour when we’ll jump to 4-digit
integers? Could someone provide a list of the successive attractors?
I guess that all integers end in a loop,
at some point. Which integer < 1000000 performs the longest “flight”? Are
there interesting sequences for the OEIS, here?
Best,
É.
(sleeping now
furiously)
__________
Update, February 23rd, 2011.
I’ve received this yesterday, from an
anonymous (Dutch?) member of SeqFans, < Aai >:
Here are some answers obtained
with progr. lang. J (http://www.jsoftware.com/index.html)
Mind line wrapping!
First different attractors N < 500
~. ,. ([: (({:=}:) ];. 1 }:) (,(+ ([: (* (_1 ^
2&|))
+/@:(,.&.":)))@{:)^:({:-.@e.}:)^:_ )&. 0+i.500
┌───────────┐
│0 │
├───────────┤
│108 99 117 │
├───────────┤
│99 117 108 │
├───────────┤
│117 108 99 │
├───────────┤
│207 198 216│
├───────────┤
│198 216 207│
├───────────┤
│216 207 198│
├───────────┤
│297 315 306│
├───────────┤
│306 297 315│
├───────────┤
│315 306 297│
├───────────┤
│405 396 414│
├───────────┤
│396 414 405│
├───────────┤
│414 405 396│
├───────────┤
│495 513 504│
├───────────┤
│504 495 513│
├───────────┤
│513 504 495│
└───────────┘
for
600000 <= N < 600200
~. ,. ([: (({:=}:) ];. 1 }:) (,(+ ([: (* (_1 ^
2&|))
+/@:(,.&.":)))@{:)^:({:-.@e.}:)^:_ )&. 600000+i.200
┌──────────────────────────────────────────────────────────────┐
│599949 599904 599940
599976 599931 599967 599922 599958 599913│
├──────────────────────────────────────────────────────────────┤
│600093 600111 600102 │
├──────────────────────────────────────────────────────────────┤
│600102 600093 600111 │
├──────────────────────────────────────────────────────────────┤
│600111 600102 600093 │
├──────────────────────────────────────────────────────────────┤
│600201 600192 600210 │
├──────────────────────────────────────────────────────────────┤
│600192 600210 600201 │
├──────────────────────────────────────────────────────────────┤
│600462 600480 600498
600471 600489 │
├──────────────────────────────────────────────────────────────┤
│600210 600201 600192 │
└──────────────────────────────────────────────────────────────┘
I assumed the longest ones will
be found somewhere between 100000 < N < 1000000 :-)
(O o, assumption is the mother of
all...)
(start
with N, count all numbers until the first repeating number)
length 698869 = 52
The whole sequence:
_13 ]\(,(+
([: (* (_1 ^ 2&|)) +/@:(,.&.":)))@{:)^:({:-.@e.}:)^:_
[698869, 698869, 698915,
698953, 698993, 699037, 699071, 699103, 699131, 699102, 699075, 699111, 699084,
699120, 699093, 699129, 699165, 699201, 699174, 699210, 699183, 699219, 699255,
699291, 699327, 699363, 699399, 699354, 699390, 699426, 699462, 699498, 699453,
699489, 699444, 699480, 699516, 699552, 699588, 699543, 699579, 699534, 699570,
699606, 699642,
699678, 699633, 699669, 699624, 699660, 699696, 699651, 699687, 699642] <-- first repeater.
Met vriendelijke groet,
=@@i
Good job, thank you Aai!
__________
Then came those
interesting comments:
Harvey P. Dale:
Here is a simple Mathematica program to
compute this sequence. By changing the second term in the second line of the
program, you can change the initial seed number. In most cases, the resulting
sequence fairly quickly devolves into a string of zeroes. If you seed it with
71, however, it produces a sequence that, after the first five initial terms,
consists of a repetitive cycle of 108, 99, 117.
nxt[n_]:=Module[{tidn=Total[IntegerDigits[n]]},If[EvenQ[tidn],n+tidn,
n-tidn]]
NestList[nxt,71,100]
Charles Greathouse :
Is there a good way to find the final cycles in Mathematica?
I know of bad ways (say, hardcode Floyd’s algorithm) and of course it could be
done manually, something like
Final[0] := {0}
Final[99] := {99, 117, 108}
Final[6732] := {6732, 6750, 6768, 6741,
6759}
Final[6642] := {6642, 6660, 6678, 6651,
6669}
. . .
Final[n_] := Final[n] = Final[nxt[n]]
but I was wondering if there’s a built-in way,
something like FixedPointList[nxt,
71] but stopping at a fixed cycle rather than fixed element.
Neil Sloane:
Start at n, let a(n) be the smallest number in
the cycle if it goes into a cycle, or -1 if it diverges. Is this sequence in
the OEIS? And if not, you know what to do!
William Keith :
Looks like none of them diverge, none go to 0 after 98, and all of them
wind up in a cycle that is fairly close by. Cycles appear to be exclusively rooted
on multiples of 9: {99, 117, 108, 99}, {198, 216, 207,
198}, {6732, 6750, 6768, 6741, 6759, 6732}, {6822, 6840, 6858, 6831, 6849,
6822}, etc. Makes sense, as sums of digits will be closed under that property,
and I’d suspect that there’s a digital criterion that will tell you where a
number goes.
Maximilian Hasler:
[Neil]:
> Start at n, let a(n)
be the smallest number in the cycle if it goes into a cycle, or -1 if it
diverges.
That sequence is a bit boring, and in
particular its first 3 lines...
Here are the
first 1000 terms:
/* return the first number seen twice when
starting with n */
{ EAI =
(n,S=[])->while(!setsearch(S,n),S=setunion(S,Set(n));n+=(-1)^(s=digsum(n))*s);n
}
/* return the loop, starting (and ending) with
the least element.
assumes that n is part of the loop */
{EAL =
(n)->n=[n];until(!n[#n]|n[#n]==n[1],n=concat(n,n[#n]+=(-1)^(s=digsum(n[#n]))*s));while(n[1]>vecmin(n),n=concat(vecextract(n,"2.."),n[2]));n
}
for(n=0,999,print1(EAL(EAI(n))[1]", "))
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 99, 0, 0, 0, 0,
0, 99, 0, 99, 99, 0, 0, 0, 0, 0, 99, 0, 99, 0, 0, 99, 0, 99, 0, 99, 0, 99, 0,
99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99,
99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99,
99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99,
99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 198, 99, 99, 99, 99, 99, 198, 99,
198, 99, 99, 99, 99, 99, 99, 99, 99, 198, 99, 198, 198, 99, 198, 99, 198, 99,
198, 99, 198, 99, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198,
198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198,
198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198,
198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198,
297, 198, 198, 198, 198, 198, 297, 198, 297, 198, 198, 198, 198, 198, 198, 198,
198, 297, 198, 297, 297, 198, 297, 198, 297, 198, 297, 198, 297, 198, 297, 297,
297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297,
297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297,
297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 297,
297, 297, 297, 297, 297, 297, 297, 297, 297, 297, 396, 297, 297, 297, 297, 297,
396, 297, 396, 297, 297, 297, 297, 297, 297, 297, 297, 396, 297, 396, 396, 297,
396, 297, 396, 297, 396, 297, 396, 297, 396, 396, 396, 396, 396, 396, 396, 396,
396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396,
396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396,
396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396, 396,
396, 396, 396, 396, 495, 396, 396, 396, 396, 396, 495, 396, 495, 396, 396, 396,
396, 396, 396, 396, 396, 495, 396, 495, 495, 396, 495, 396, 495, 396, 495, 396,
495, 396, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495,
495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495,
495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495,
495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 495, 594, 495,
495, 495, 495, 495, 594, 495, 594, 495, 495, 495, 495, 495, 495, 495, 495, 594,
495, 594, 594, 495, 594, 495, 594, 495, 594, 495, 594, 495, 594, 594, 594, 594,
594, 594, 594, 594, 594, 594, 594, 594, 594, 594, 594, 594, 594, 594, 693, 594,
594, 594, 594, 594, 594, 594, 594, 594, 594, 594, 594, 594, 594, 594, 594, 594,
594, 594, 693, 594, 594, 594, 594, 594, 594, 594, 594, 594, 594, 594, 594, 594,
594, 594, 594, 594, 594, 594, 594, 594, 693, 594, 594, 594, 594, 594, 693, 594,
693, 594, 594, 594, 594, 594, 594, 594, 594, 693, 594, 693, 693, 594, 693, 594,
693, 594, 693, 594, 693, 594, 693, 693, 693, 693, 693, 693, 693, 693, 693, 693,
693, 693, 693, 693, 693, 693, 693, 693, 792, 693, 693, 693, 693, 693, 693, 693,
693, 693, 693, 693, 693, 693, 693, 693, 693, 693, 693, 693, 792, 693, 693, 693,
693, 693, 693, 693, 693, 693, 693, 693, 693, 693, 693, 693, 693, 693, 693, 693,
693, 693, 792, 693, 693, 693, 693, 693, 792, 693, 792, 693, 693, 693, 693, 693,
693, 693, 693, 792, 693, 792, 792, 693, 792, 693, 792, 693, 792, 693, 792, 693,
792, 792, 792, 792, 792, 792, 792, 792, 792, 792, 792, 792, 792, 792, 792, 792,
792, 792, 972, 792, 792, 792, 792, 792, 792, 792, 792, 792, 792, 792, 792, 792,
792, 792, 792, 792, 792, 792, 972, 792, 792, 792, 792, 792, 792, 792, 792, 792,
792, 792, 972, 792, 792, 792, 792, 792, 792, 792, 972, 792, 972, 792, 792, 792,
792, 792, 972, 792, 972, 792, 792, 792, 792, 792, 792, 792, 792, 972, 792, 972,
972, 792, 972, 792, 972, 792, 972, 792, 972, 792, 972, 972, 972, 972, 972, 972,
972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972,
972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972,
972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972,
972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972,
972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972,
972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972,
972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972,
972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972,
972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972,
972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972, 972,
972, 972, 972, 972, ...
Maybe more / also interesting:
b(n) = list of these values
c(n) = least integer to hit b(n)
d(n) = largest integer to hit b(n)
e(n) = number of steps for n to go to a(n)
f(n) = number of steps until one element is seen
twice
g(n) = number of steps until / before n reaches it’s "ending loop"
h(n) = length of the loop containing b(n)
Maximilian again:
The loops and the minimal element going into that loop:
L=[]; for(n=0,9999,T=EAL(EAI(n)); setsearch(L,T) & next; print(n"
"T","); L=setunion(L,Set([T])))
0 [0, 0],
71 [99, 117, 108, 99],
170 [198, 216, 207, 198],
260 [297, 315, 306, 297],
350 [396, 414, 405, 396],
440 [495, 513, 504, 495],
530 [594, 612, 603, 594],
578 [693, 711, 702, 693],
668 [792, 810, 801, 792],
758 [972, 990, 1008, 999, 972],
1070 [1098, 1116, 1107, 1098],
1160 [1197, 1215, 1206, 1197],
1250 [1296, 1314, 1305, 1296],
1340 [1395, 1413, 1404, 1395],
1430 [1494, 1512, 1503, 1494],
1478 [1593, 1611, 1602, 1593],
1568 [1692, 1710, 1701, 1692],
1658 [1962, 1980, 1998, 1971, 1989, 1962],
2060 [2097, 2115, 2106, 2097],
2150 [2196, 2214, 2205, 2196],
2240 [2295, 2313, 2304, 2295],
2330 [2394, 2412, 2403, 2394],
2378 [2493, 2511, 2502, 2493],
2468 [2592, 2610, 2601, 2592],
2558 [2862, 2880, 2898, 2871, 2889, 2862],
2837 [2952, 2970, 2988, 2961, 2979, 2952],
3050 [3096, 3114, 3105, 3096],
3140 [3195, 3213, 3204, 3195],
3230 [3294, 3312, 3303, 3294],
3278 [3393, 3411, 3402, 3393],
3368 [3492, 3510, 3501, 3492],
3458 [3762, 3780, 3798, 3771, 3789, 3762],
3737 [3852, 3870, 3888, 3861, 3879, 3852],
3836 [3942, 3960, 3978, 3951, 3969, 3942],
4040 [4095, 4113, 4104, 4095],
4130 [4194, 4212, 4203, 4194],
4178 [4293, 4311, 4302, 4293],
4268 [4392, 4410, 4401, 4392],
4358 [4662, 4680, 4698, 4671, 4689, 4662],
4637 [4752, 4770, 4788, 4761, 4779, 4752],
4736 [4842, 4860, 4878, 4851, 4869, 4842],
4844 [4932, 4950, 4968, 4941, 4959, 4932],
5030 [5094, 5112, 5103, 5094],
5078 [5193, 5211, 5202, 5193],
5168 [5292, 5310, 5301, 5292],
5258 [5562, 5580, 5598, 5571, 5589, 5562],
5537 [5652, 5670, 5688, 5661, 5679, 5652],
5636 [5742, 5760, 5778, 5751, 5769, 5742],
5744 [5832, 5850, 5868, 5841, 5859, 5832],
5843 [5922, 5940, 5958, 5931, 5949, 5922],
6020 [6093, 6111, 6102, 6093],
6068 [6192, 6210, 6201, 6192],
6158 [6462, 6480, 6498, 6471, 6489, 6462],
6437 [6552, 6570, 6588, 6561, 6579, 6552],
6536 [6642, 6660, 6678, 6651, 6669, 6642],
6644 [6732, 6750, 6768, 6741, 6759, 6732],
6743 [6822, 6840, 6858, 6831, 6849, 6822],
6842 [6912, 6930, 6948, 6921, 6939, 6912],
6950 [7092, 7110, 7101, 7092],
7058 [7362, 7380, 7398, 7371, 7389, 7362],
7337 [7452, 7470, 7488, 7461, 7479, 7452],
7436 [7542, 7560, 7578, 7551, 7569, 7542],
7544 [7632, 7650, 7668, 7641, 7659, 7632],
7643 [7722, 7740, 7758, 7731, 7749, 7722],
7742 [7812, 7830, 7848, 7821, 7839, 7812],
7854 [7902, 7920, 7938, 7911, 7929, 7902],
7931 [8262, 8280, 8298, 8271, 8289, 8262],
8237 [8352, 8370, 8388, 8361, 8379, 8352],
8336 [8442, 8460, 8478, 8451, 8469, 8442],
8444 [8532, 8550, 8568, 8541, 8559, 8532],
8543 [8622, 8640, 8658, 8631, 8649, 8622],
8642 [8712, 8730, 8748, 8721, 8739, 8712],
8754 [8802, 8820, 8838, 8811, 8829, 8802],
8893 [9162, 9180, 9198, 9171, 9189, 9162],
9137 [9252, 9270, 9288, 9261, 9279, 9252],
9236 [9342, 9360, 9378, 9351, 9369, 9342],
9344 [9432, 9450, 9468, 9441, 9459, 9432],
9443 [9522, 9540, 9558, 9531, 9549, 9522],
9542 [9612, 9630, 9648, 9621, 9639, 9612],
9654 [9702, 9720, 9738, 9711, 9729, 9702],
9883 [9999, 10035, 10026, 10017, 10008, 9999],
Maximilian, follow up:
>>> f(n) =
number of steps until one element is seen twice
{ EAC = (n,S=[])->for(i=1,1e9,
S=setunion(S,Set(n));setsearch(S,n+=(-1)^(s=digsum(n))*s) &
return(i))
}
for(n=0,299, print1(EAC(n)", "))
1, 2, 6, 2, 5, 2, 4, 2, 4, 2, 3, 7, 3, 6, 3, 5, 3, 5, 3, 5, 8, 4, 7, 4,
6, 4, 6, 4, 6, 4, 5, 8, 5, 12, 5, 7, 5, 7, 5, 11, 9, 6, 13, 6, 8, 6, 8, 6, 12,
6, 7, 10, 7, 9, 7, 9, 7, 9, 7, 12, 11, 8, 10, 8, 10, 8, 10, 8, 13, 8, 9, 8, 9,
11, 9, 11, 9, 9, 9, 7, 6, 10, 12, 10, 12, 10, 5, 10, 5, 10, 11, 8, 11, 6, 11,
6, 11, 5, 11, 3, 4, 7, 4, 6, 4, 5, 4, 5, 3, 5, 7, 4, 6, 4, 5, 4, 5, 3, 5, 4, 4,
7, 4, 11, 4, 6, 4, 6, 4, 10, 8, 5, 12, 5, 7, 5, 7, 5, 11, 5, 6, 9, 6, 8, 6, 8,
6, 8, 6, 11, 10, 7, 9, 7, 9,
>>> Records:
m=0; for(n=0,999999, m<EAC(n)|next;
print1(m=EAC(n) ", "))
1, 2, 6, 7, 8, 12, 13, 14, 20, 27, 28, 31, 36,
37, 38, 39, 40, 41, 45, 46, 48, 49, 52
>>> Indices of records:
0, 1, 2, 11, 20, 33, 42, 161, 758, 1658, 7931, 29773, 29782, 79811,
289474, 289511, 299374, 299411, 389374, 389411, 399274, 399311, 698869 (answer to Eric’s question: record holder below
10^6)
>>> Indices with yet unseen run length:
u=0; for(n=0,999999, bittest(u,EAC(n)) & next; print1([n, m=EAC(n)] ",
"); u+=1<<m)
[0, 1], [1, 2], [2, 6], [4, 5], [6, 4], [10,
3], [11, 7], [20, 8], [33, 12], [39, 11], [40, 9], [42, 13], [51, 10], [161,
14], [758, 20], [778, 19], [790, 18], [798, 17], [820, 16], [828, 15], [1658,
27], [1678, 26], [1690, 25], [1698, 24], [1719, 21], [1720, 23], [1728, 22],
[7931, 28], [29773, 31], [29782, 36], [29801, 30], [29810, 35], [29821, 29],
[29830, 34], [29852, 33], [29878, 32], [79811, 37], [289474, 38], [289511, 39],
[299374, 40], [299411, 41], [389374, 45], [389408, 44], [389411, 46], [389419,
42], [389440, 43], [399274, 48], [399308, 47], [399311, 49], [698869, 52],
[698896, 50], [698915, 51]
>>> Least k such that f(k)=n, [or -1 if n never occurs in f: will this happen?]
apply(x->x[1], vecsort(%,2));
0, 1, 10, 6, 4, 2, 11, 20, 40, 51, 39, 33, 42, 161, 828, 820, 798, 790,
778, 758, 1719, 1728, 1720, 1698, 1690, 1678, 1658, 7931, 29821, 29801, 29773,
29878, 29852, 29830, 29810, 29782, 79811, 289474, 289511, 299374, 299411,
389419, 389440, 389408, 389374, 389411, 399308, 399274, 399311, 698896, 698915,
698869
Robert Gerbicz:
[Neil]:
> Start at n, let a(n) be the smallest
number in the cycle if it goes into a cycle, or -1 if it diverges.
My conjecture is that for every n in O(log(n)^2)
iteration the sequence goes to a cycle. The idea behind this that by O(1/log(n)) probability F(F(n))=n is true. Computations up
to n=10^5 supports my conjecture.
Robert Gerbicz, again:
> The idea behind this that by O(1/log(n))
probability F(F(n))=n is true.
Need another idea, up to n=10^7 there is no solution of F(F(n))=n, other than the trivial n=0.
Does it have a loop of length two?
Hans Havermann:
[Robert Gerbicz]:
> Does it have a loop of length two?
No. Let {a,b}
represent such a loop with a<b.
b=a+s(a)
a=b-s(b) => b=a+s(b)
=> s(a)=s(b)
but s(a) is even and s(b) is odd, a contradiction
Jack Brennen:
[Neil]:
> Start at n, let a(n) be the smallest
number in the cycle if it goes into a cycle, or -1 if it diverges.
Cycles must consist exclusively of multiples of 9.
Any time that a number’s successor is smaller than the first number, the
successor will be a multiple of 9. Any multiple of 9 has a successor which is a
multiple of 9. Every cycle will have a downward step in the cycle. Put all that
together, it’s easy to see that all cycles are entirely multiples of 9.
Jack Brennen:
[Robert Gerbicz]:
> Need another idea, up to n=10^7 there is
no solution of F(F(n))=n, other than the trivial n=0.
> Does it have a loop of length two?
There is no other solution of F(F(n))=n, other
than the trivial 0.
The sequence can only go up by an even delta, and only down by an odd
delta. So no two-step cycles, since one would have to be an up delta, and the
other a down delta.
A three-step cycle would have to be UP, DOWN, DOWN. For instance,
99->117->108->99.
Jack Brennen, follow up:
I wrote a little program to find invariants for loops... Basically, the
idea being that there should be invariants of the form:
N*10^a + b always ends up in
the same loop as long as the sum of digits of N is equal to some value C.
The first such invariant that the program found was C=16, a=2, b=2.
The first such integer example under this invariant is the number 7902:
7902->7920->7938->7911->7929->7902.
Note that since the additions and subtractions never carry or borrow
beyond the tens column, all that matters is the digit sum of the prefix (in
this case "79" has digit sum 16). So the following numbers all enter
similar loops:
7902, 8802, 9702, 16902, 17802,
18702, 19602, 25902, 26802, 27702, 28602, 29502, ...
Another example, with a large prefix digit sum, is C=100, a=3, b=332.
If N has digit sum 100, the following loop is possible:
N*10^3 + 332
N*10^3 + 440
N*10^3 + 548
N*10^3 + 431
N*10^3 + 539
N*10^3 + 422
N*10^3 + 530
N*10^3 + 638
N*10^3 + 521
N*10^3 + 629
N*10^3 + 512
N*10^3 + 620
N*10^3 + 728
N*10^3 + 611
N*10^3 + 719
N*10^3 + 602
N*10^3 + 710
N*10^3 + 818
N*10^3 + 701
N*10^3 + 809
N*10^3 + 692
N*10^3 + 575
N*10^3 + 458
N*10^3 + 341
N*10^3 + 449
N*10^3 + 332
The loop has 25 steps in a cycle, 13 steps are each +108, the other 12 steps are each -117.
Seems obvious that you could find arbitrarily long loops, although you
would obviously be dealing with long numbers. The loop shown above doesn’t
apply to any integer smaller than 199999999999332.
Maximilian Hasler:
[Jack Brennen]:
Nice reasoning of yours, abt. multiples of 9.
Just fyi, some
experimental data (loops) [above].
You will see & may want to proof some patterns (last digit of
elements in a loop, depending on length, especially for L=5)
Aai:
Hi Eric,
The following is obtained by using the J programming language.
Let’s call the canonical form of a terminating cycle the rotation that
starts with the smallest value, e.g. 71 has the first 3-cycle:
108 99 117
having the canonical form
99 117 108
Then 99 is smallest number of this cycle.
Of course this cycle has the following three instances
99 117 108
117 108 99
108 99 117
Here are the first 100 terms for 0 <= N <= 12230:
0, 99, 198, 297, 396, 495, 594, 693,
792, 972, 1098, 1197, 1296, 1395, 1494, 1593, 1692, 1962, 2097, 2196, 2295,
2394, 2493, 2592, 2862, 2952, 3096, 3195, 3294, 3393, 3492, 3762, 3852, 3942,
4095, 4194, 4293, 4392, 4662, 4752, 4842, 4932, 5094, 5193, 5292, 5562, 5652,
5742, 5832, 5922, 6093, 6192, 6462, 6552, 6642, 6732, 6822, 6912, 7092, 7362,
7452, 7542, 7632, 7722, 7812, 7902, 8262, 8352, 8442, 8532, 8622, 8712, 8802,
9162, 9252, 9342, 9432, 9522, 9612, 9702, 9999, 10098, 10197, 10296, 10395,
10494, 10593, 10692, 10962, 11097, 11196, 11295, 11394, 11493, 11592, 11862,
11952, 12096, 12195, 12294, ...
having digit sums 0 18 36
Cycle starting values for 500000 <= N < 510000
499914 500094 500193 500292 500562 500652
500742 500832 500922 501093 501192 501462
501552 501642 501732 501822 501912 502092
502362 502452 502542 502632 502722 502812
502902 503262 503352 503442 503532 503622
503712 503802 504162 504252 504342 504432
504522 504612 504702 505062 505152 505242
505332 505422 505512 505602 506052 506142
506232 506322 506412 506502 507042 507132
507222 507312 507402 507879 508032 508122
508212 508302 508779 508878 509022 509112
509202 509679 509778 509877 509994 510093
The digits sums of these values are: 36 18
Q: are all digit sums of these values even multiples of 9?
Jean-Marc Falcoz:
Voici deux images faites avec Mathematica, qui regroupent synthétiquement les chaînes formées par tous les entiers, de 0 à 100.
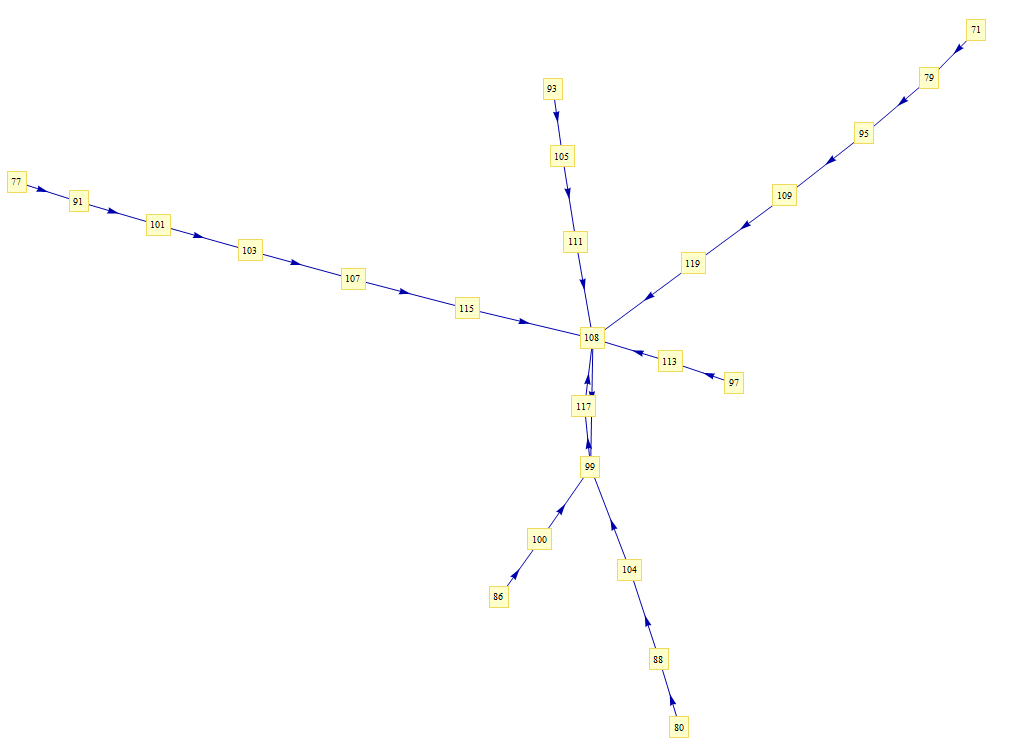
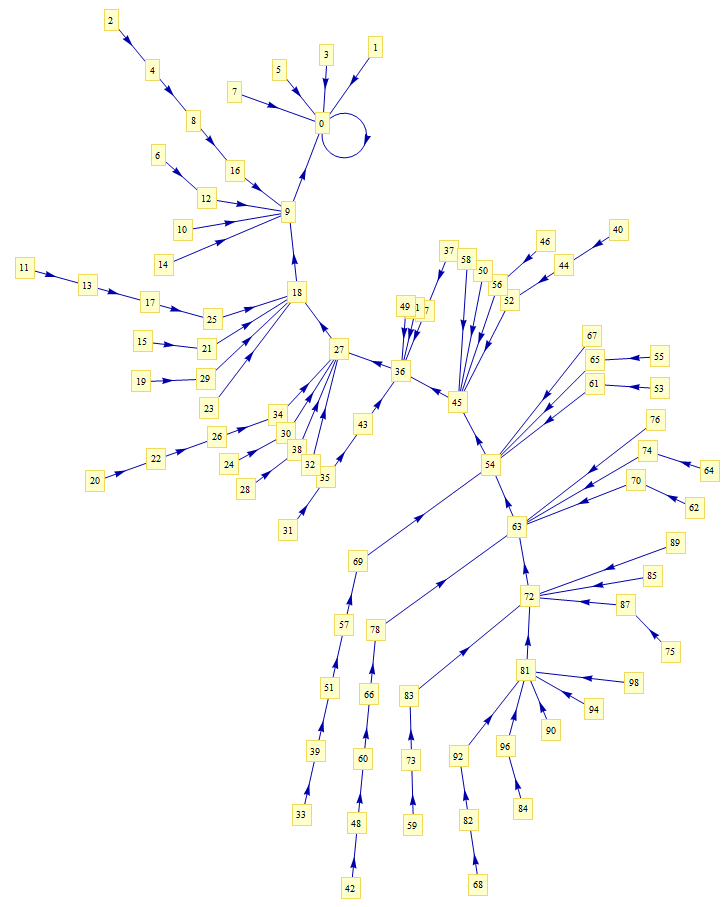
Hans Havermann:
Known
minimal solutions for a given loop-length, in the order
in which they arise:
1 {0}
3 {99, 117, 108}
4 {972, 990, 1008, 999}
5 {1962, 1980, 1998, 1971, 1989}
7 {39879, 39915, 39888, 39924, 39897, 39933, 39906}
6 {99954, 99990, 100026, 100017, 100008, 99999}
8 {299934, 299970, 300006, 299997, 299952, 299988, 299943, 299979}
9 {399924, 399960, 399996, 399951, 399987, 399942, 399978, 399933,
399969}
10 {29999916, 29999970, 30000024, 30000015, 30000006, 29999997, 29999934,
29999988, 29999925, 29999979}
11 {39999906, 39999960, 40000014, 40000005, 39999996, 39999933, 39999987,
39999924, 39999978, 39999915, 39999969}
13 {49999806, 49999860, 49999914, 49999968, 49999905, 49999959, 49999896,
49999833, 49999887, 49999824, 49999878, 49999815, 49999869}
14 {2999999808, 2999999880, 2999999952, 3000000024, 3000000015,
3000000006, 2999999997, 2999999916, 2999999988, 2999999907, 2999999979,
2999999898, 2999999817, 2999999889}
12 {3989999808, 3989999880, 3989999952, 3990000024, 3989999997,
3989999916, 3989999988, 3989999907, 3989999979, 3989999898, 3989999817, 3989999889}
17 {3999999708, 3999999780, 3999999852, 3999999924, 3999999996,
3999999915, 3999999987, 3999999906, 3999999978, 3999999897, 3999999816,
3999999888, 3999999807, 3999999879, 3999999798, 3999999717, 3999999789}
With the
exception of length-12, the larger solutions are all in the space directly
below m*10^n (m=1..9), so using this as a search
mechanism, some other loop-lengths and the first element of the (not
necessarily minimal) loop:
23 19999999998909
25 99999999999432
16 5999999999998824
29 7999999999999524
19 89999999999899767
15 99999999999899766
20 499999999999989924
33 699999999999999516
37 69999999999999999318
41 19999999999999999899360
49 99999999999999999999999144
31 2999999999999999999999899575
53 7999999999999999999999999326
27 89999999999999999999999899578
57 899999999999999999999999999028
24 2999999999999999999999999999988864
69 2999999999999999999999999999999996334
73 99999999999999999999999999999999899226
35 1999999999999999999999999999999999899369
77 19999999999999999999999999999999999899207
81 2999999999999999999999999999999999999996460
28 199999999999999999999999999999999999999988802
32 899999999999999999999999999999999999999988957
93 1999999999999999999999999999999999999999999899216
97 99999999999999999999999999999999999999999999899298
22 29999999999999999999999999999999999999999999999999998548
48 899999999999999999999999999999999999999999999999999981604
56 999999999999999999999999999999999999999999999999999980604
137 29999999999999999999999999999999999999999999999999999999999999999995038
40
19999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999981800
92
19999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999981206
No sign of 18, 21, 26, ...
The solutions for loop-lengths 16, 19, 15, 40, and 92 were first noted
by Lars Blomberg.
Hans Havermann, follow-up:
In our known minimal solutions for a given loop-length, many (lengths
3, 4, 6, 8, 10, 11, 14) have loop members on both sides of the m*10^n
reference point. By contrast, in the
subsequent not-necessarily-
minimal solutions only one (length-22)
meets this consideration. With
that caveat
in mind, it is nevertheless much easier to search for new
lengths based on just such a criterion: One
need only determine the
loop starting with ‘(m)zeros(9-m)’ and take its
smallest member. Doing
so for n up to 10000 yields 8 new loop-lengths:
18, 26, 39, 21, 36,
43, 30, and 34 (leaving 38 the smallest loop-length with no known
upper bound). The first members of these new loops
are quite large:
34’s is an 8779-digit number! Because it is on the smaller end of that
scale, I’ll evolve loop-length 18 here:
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999995547
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999997023
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999995556
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999997032
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999995565
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999997041
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999995574
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999997050
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999995583
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999997059
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999998535
7000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000011
7000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000002
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999993
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999998508
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999984
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999998499
6999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999997014
Lars Blomberg:
Using a technique which I guess is
similar to the one Hans described
lately, namely, to iterate only the small values to the right and keep track of
the total DigitSum
without actually computing with these enormous numbers, I can supply the
following:
An
18-loop:
599999999899999999959
599999999900000000139
599999999900000000040
599999999900000000130
599999999900000000220
599999999900000000310
599999999900000000400
599999999900000000490
599999999900000000391
599999999900000000292
599999999900000000193
599999999900000000094
599999999899999999995
599999999900000000175
599999999900000000076
599999999899999999977
599999999900000000157
599999999900000000058
A 38-loop, starting with
4999989999999999999999999999999999999618
Using a shorthand notation where
<n> means n 9’s in sequence, this can more conveniently be expressed as
4<4>8<31>618
This 293-loop is the longest I have
found so far:
5<144>(30)1246
where (n) means
n 0’s in sequence
And this 186-loop has the largest
starting value (610 digits) that I have found:
8<343>8<261>3368
None of the above loops are proven to
have the smallest starting number for that loop-length.
Lars Blomberg, update (March 17th, 2011)
Colorless integers -- An enumerator for a
series of cycles of length 3
The first cycle of length 3 is {99, 117, 108} with the differences between consecutive values being
{18, -9, -9}.
There are many other cycles of length 3
with the same differences but with different start values.
The first few cycle start values are:
{99, 198, 297, 396, 495, 594, 693, 792,
1098, 1197, 1296, 1395, 1494,
1593, 1692, 2097, 2196, 2295, 2394, 2493,
2592, 3096, 3195, 3294, 3393,
3492, 4095, 4194, 4293, 4392, 5094, 5193,
5292, 6093, 6192, 7092, 10098,
10197, 10296, 10395, 10494, 10593, 10692, 11097, ...}
Taking first differences and dividing by 9
we get (all the values are divisible by 9 so the differences are too):
{11, 11, 11, 11, 11, 11, 11, 11, 34, 11,
11, 11, 11, 11, 11, 45, 11, 11, 11, 11,
11, 56, 11, 11, 11, 11, 67, 11, 11, 11,
78, 11, 11, 89, 11, 100, 334, 11, 11,
11, 11, 11, 11, 45, ...}
There is a pattern here in the differences that becomes more obvious as more values are
inspected.
After some coding and testing, the
following algorithm was found. It is expressed in C#, but it should be
understandable since it contains no difficult language features.
List<long> All = new List<long>();
// Creates the
list "All" with differences divided by 9
// Parameter "maxSize"
is maximum number of digits in the generated differences
public
void Create(int
maxSize)
{
Start();
for
(int
i = 2; i <= maxSize; i++)
{
GenerateSize(i);
}
}
// A few values in the beginning cannot
be made to fit the algorithm
private
void Start()
{
for
(int
i = 0; i < 8; i++)
{
All.Add(11);
}
}
// Generate
everything for a given size
void
GenerateSize(int size)
{
for
(int
i = 4; i <= 10; i++)
{
Generate(i,
size, true);
}
}
// Recursive method
void
Generate(int
lastDigit, int size, bool startWithNumber)
{
int
i, j;
if
(startWithNumber)
{
All.Add(Number(lastDigit,
size));
}
if
(size > 2)
{
bool
swn = false;
for
(i = lastDigit; i < 11;
i++)
{
Generate(i,
size - 1, swn);
swn
= true;
}
}
else
{
// Just a
number of 11's
for
(j = lastDigit; j < 10;
j++)
{
All.Add(11);
}
}
}
// For example, calling with lastDigit=4 and size=5 will return the number 33334
long
Number(int
lastDigit, int size)
{
return
long.Parse(new
string((char)('0' + lastDigit - 1), size))+1;
}
Looking at the # of digits in the start
value versus the first digit of the start value we get the following table:
# of digits->
Below:
Initial digit
2 3 4 5 6 7 8 9 10 11 12
1 1 7 28 84 210
462 924 1716 3003 5005
2 1 6 21 56 126 252 462 792 1287 2002
3 1 5 15 35 70 126 210 330 495 715
4 1 4 10 20 35 56 84 120 165 220
5 1 3 6 10 15 21 28 36 45 55
6 1 2 3 4 5 6 7 8 9 10
7 1 1 1 1 1 1 1 1 1 1
9 1
We see that cycles with low initial digit
are more frequent, and increasingly so as the number of digits grow larger.
One can note that initial digit 7 has just
one value per order of magnitude (of the form 70...092), 8 has
none at all and 9 none at all except the very first cycle (99).
Furthermore, one can count all the cycles
starting from a number with a given number of digits.
# of digits 2 3 4 5 6
7 8 9 10 11 12
Count 1 7 28 84 210 462 924 1716 3003 5005 8008
Accumulated count 1
8 35 112 294 672 1386 2640 4719 8008 13013
With the help of OEIS, it is easy to find
that the "Count" values are:
A000579, binomial coefficients C(n,6), a(n) = (n^6-15*n^5+85*n^4-225*n^3+274*n^2-120*n)/720.
And the "Accumulated count"
values are:
A040977, C(n+5,5)*(n+3)/3,
Sequence is n^2*(n^2-1)*(n^2-4)/360 if offset 3.
This indicates that the number of 3-cycles
with differences {18, -9, -9} are infinite, but they become increasingly rare: O(n^6)/10^n.
All of the above has come from empirical
study, I have no proofs.
Hans also asked me to inform you that he has
added loop evolution to the up-to-100 loops page:
http://chesswanks.com/seq/ColorlessMinima.txt
__________
Many thanks
to all contributors!
Best,
É.
__________
Nage
en petits bassins
... on voit bien les entiers, comme autant de billes de verre,
rouler dans un paysage de porcelaine,
dévaler certaines pentes, hésiter,
puis se répartir doucement dans une infinité de bassins d’attraction,
se serrer les uns contre les autres, en spirale,
au bout du labyrinthe des collines et vallées.
[É.A., private e-mail to Alexandre
Wajnberg]