Colour, drag and drop sequence
Modus
operandi:
Write
the seq. N of the natural numbers:
N = 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
36 37 38 39 40 41 42 43 44 45 ...
Start
with n=1 and apply the following rules to N:
Rule one: at step ‘n’ colour in yellow ‘n’ and in grey the nth integer at the
right of ‘n’.
Rule two: drag and drop the
grey integer next to the yellow integer (right-side) and keep the rest of the
sequence as it is.
Rule three:
make ‘n’=‘n’+1 then go back to Rule one
and apply again to the re-ordered set of Naturals.
[The
first column on the left (in blue) shows the step of the computation]
1 1 2 3
4 5 6
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 ...
2 1 2 3 4 5
6 7 8 9 10
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
37 38 39 40 41 42 43 44 45 ...
3 1 2 4 3 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 ...
4 1 2 4 3 7 5 6 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 ...
5 1 2 4 6
3 7 5 8 9 10 11 12 13 14 15 16 17 18
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44
45 ...
6 1 2
4 6 3 7 5
12 8
9 10 11 13 14 15 16 17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 ...
7 1 2
4 6 9
3 7 5 12 8 10 11 13 14 15
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41
42 43 44 45 ...
8 1 2
4 6 9 3 7 14
5 12 8 10 11 13 15 16 17 18 19 20 21
22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 ...
9 1 2
4 6 9 3 7 14 5
12 8 19 10 11 13
15 16 17 18 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41
42 43 44 45 ...
10 1
2 4 6 9
11 3
7 14 5 12 8 19 10 13 15 16 17 18 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 ...
11 1
2 4 6 9 11 3 7
14 5 12
8 19 10 24 13 15 16 17 18 20 21 22
23 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 ...
12 1
2 4 6 9 11
15 3
7 14 5 12 8
19 10 24 13 16 17 18 20 21 22 23 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 ...
13 1
2 4 6 9 11
15 3
7 14 5 12 23 8 19 10 24 13 16 17 18 20 21 22 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 ...
14 1
2 4 6 9 11
15 3
7 14 5 12 23
8 19 10 24 13 31 16 17 18 20 21 22 25 26 27 28 29
30 32 33 34 35 36 37 38 39 40 41 42 43 44 45 ...
15 1
2 4 6 9 11
15 3 7 14
21 5 12 23 8 19 10 24 13 31 16 17 18
20 22 25 26 27 28 29 30 32 33 34 35 36 37 38 39 40 41 42 43 44 45 ...
16 1
2 4 6 9 11
15 17 3 7 14 21
5 12 23 8 19 10 24 13 31 16 18 20 22 25 26 27 28
29 30 32 33 34 35 36 37 38 39 40 41 42 43 44
45 ...
17 1
2 4 6 9 11
15 17 3 7 14
21 5 12 23 8 19 10 24 13 31 16 38 18 20 22 25 26 27 28 29 30 32 33 34 35 36 37 39 40 41 42 43 44
45 ...
18 1
2 4 6 9 11
15 17 20 3 7 14 21
5 12 23 8 19 10 24 13 31 16 38 18 22 25 26 27 28 29 30
32 33 34 35 36 37 39 40 41 42 43 44 45 ...
19 1
2 4 6 9 11
15 17 20 3 7 14 21
5 12 23 8 19 10 24 13 31 16 38 18 43 22 25 26
27 28 29 30 32 33 34 35 36 37 39 40 41 42
44 45 ...
20 1
2 4 6 9 11
15 17 20 3 7 14
21 5 12 23 8 19 35 10 24 13 31 16 38 18 43 22 25 26 27 28 29 30 32 33 34 36 37 39 40 41 42 44 45 ...
21 1
2 4 6 9 11
15 17 20 25 3 7 14 21 5 12
23 8 19 35 10 24 13 31 16 38 18 43 22 26
27 28 29 30 32 33 34 36 37 39 40 41 42 44 45 ...
22 1
2 4 6 9 11
15 17 20 25 3 7 14 21 32 5 12 23
8 19 35 10 24 13 31 16 38 18 43 22 26 27 28 29 30 33 34 36 37 39 40 41 42 44 45
...
... etc.
Emerging
sequence : 1, 2, 4, 6, 9, 11, 15, 17, 20, 25 ...
(which is monotonically increasing -- poor 3 and 5 and 7 and 8, etc.!)
Could
someone please compute a few more terms of this (very slow emerging) sequence?
Best,
É.
__________
Update,
July 10th, 2009 --> 15:45, Brussels time:
I’ve
received this very neat answer from Pr.
Dr. Alois Heinz a couple of minutes ago:
> The first 155 items:
1, 2, 4, 6, 9, 11, 15, 17, 20, 25, 27, 29,
33, 36, 40, 42, 46, 49, 51, 54, 60, 63, 65, 68, 70, 75, 77, 82, 85, 89, 92, 94,
97, 101, 103, 106, 110, 113, 115, 118, 125, 127, 132, 134, 136, 140, 143, 146,
148, 153, 157, 159, 162, 165, 169, 173, 178, 180, 182, 186, 189, 191, 194, 197,
202, 204, 206, 208, 214, 220, 224, 226, 229, 234, 236, 240, 243, 245, 247, 249,
252, 259, 262, 264, 268, 271, 274, 277, 281, 283, 287, 289, 291, 295, 299, 303,
306, 311, 315, 317, 321, 323, 325, 330, 332, 335, 339, 343, 345, 347, 350, 353,
360, 363, 367, 370, 373, 376, 379, 382, 387, 390, 392, 395, 399, 402, 405, 407,
410, 412, 417, 421, 429, 431, 434, 436, 438, 441, 444, 447, 449, 451, 454, 457,
461, 463, 469, 474, 479, 482, 485, 489, 492, 494, 498, ...
... thank you, Alois !
Grüsse,
É.
__________
Update, February 21st, 2011
I’ve received this interesting comment and illustration from Jean-Marc Falcoz (in French):
J’ai calculé un peu plus de 18000
termes (plusieurs heures de machine) ; on constate que a(n) semble
s’approcher asymptotiquement de 3,284...* n. Le graphe de la suite n’est pas
très intéressant, car il est très proche de celui de la droite f(x) =
x*3,284...
Par contre le graphe de a(n)/n est
sympa, car on voit la convergence asymptotique.
En illustration : les termes et
le graphe de a(n)/n (l’axe des x ne part pas de l’origine, et il y a un rapport
d’environ 6000000 entre les échelles des axes, sinon on ne verrait rien du tout
!)
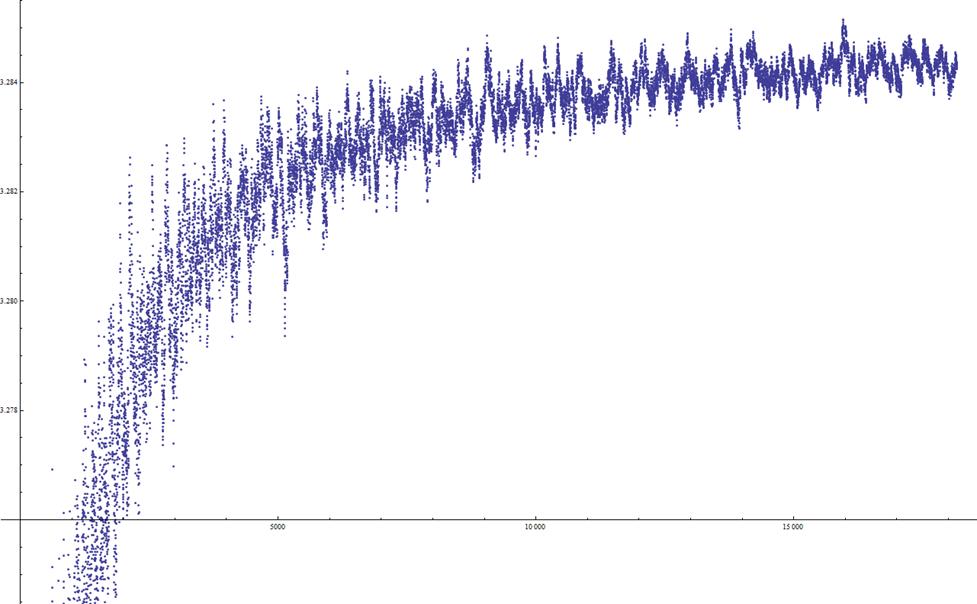
a(n)/n graph
__________
Merci beaucoup, Jean-Marc — magnifique travail, comme d’habitude!
(back to main page, là
)