Combing the Primes
Let’s
try to give to the prime numbers another “address” than their usual one.
Today’s address is their rank
in the Naturals:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 ...
We
will use a series of multiple “combs” to locate the primes.
Our
1st comb has 2 spaces
between each tooth. We place the first tooth on zero:
0 1 2
3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 ...
|_____|_____|_____|_____|_____|_____|_____|_____|_____|_____|_____|_____|_____|_____|_____|_____|_____|_____|_____|_____|_____|_____|_____|_____|___
...
Our
2nd comb has 4 spaces
between each tooth. We place the first tooth on the first previously uncombed integer yet -- one:
0 1
2 3 4 5
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 ...
|___________|___________|___________|___________|___________|___________|___________|___________|___________|___________|___________|___________|___
...
Our
3rd comb has 8 spaces
between each tooth. We place the first tooth on the first uncombed integer yet,
as usual -- three:
0
1 2 3 4
5 6 7
8 9 10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29 30 31
32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 ...
|_______________________|_______________________|_______________________|_______________________|_______________________|_______________________|___
...
Our
4th comb has 16 spaces
between each tooth. We place the first tooth on the first uncombed integer yet
-- seven:
0
1 2 3
4 5 6 7
8 9 10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29 30 31
32 33 34 35 36 37 38 39 40 41 42 43
44 45 46 47 48 49 50 51 ...
|_______________________________________________|_______________________________________________|_____________________________________
...
Our
5th comb has 32 spaces
between each tooth. We still place the first tooth on the first uncombed
integer yet -- fifteen:
0
1 2 3
4 5 6
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
37 38 39 40 41 42 43 44 45 46 47 48
49 50 51 ...
|_______________________________________________________________________________________________|_____________
...
... etc. As one knows, this way of defining combs is the most
economical one in order to punch
every integer with the minimum set of different
combs. (Most of you have already noticed that the nth comb has its first tooth on [(2^(n-1))-1]
and has [(2^n)-1] spaces between each tooth).
Let's
now give to each prime a P(n,y)
address with n=(the nth
comb) and y=(the yth
tooth on that comb). We’ll then produce this table:
2-->(1,2) 23-->(4,2) 59-->(3,8)
3-->(3,1) 29-->(2,8) 61-->(2,16)
5-->(2,2) 31-->(6,1) 67-->(3,9)
7-->(4,1) 37-->(2,10) 71-->(4,4)
11-->(3,2)
41-->(2,11)
73-->(2,19)
13-->(2,4) 43-->(3,6) 79-->(5,3)
17-->(2,5)
47-->(5,2)
83-->(3,11)
19-->(3,3)
53-->(2,14)
97-->(2,25) etc.
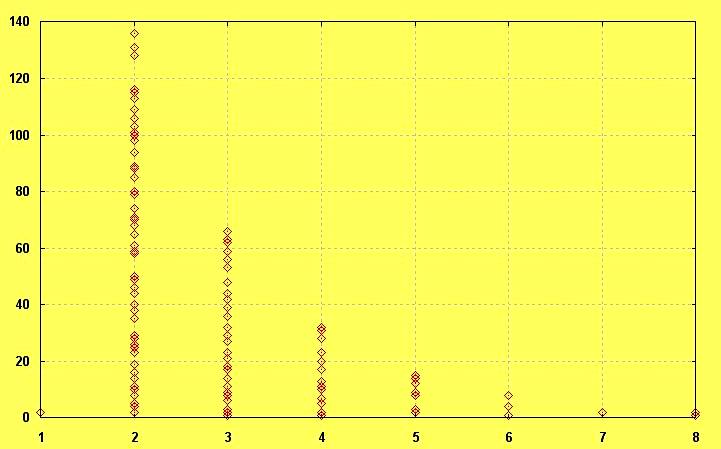
Jacques Tramu computed and drew the first hundred primes in (n,y) Cartesian coordinates: does something interesting
appear?
I’m
not sure... ;-?
Best,
É.