Hello SQeqFan and Math-fun ;

Decimation-like sequences

Hello SeqFan and Math-fun ;

(sorry if this is old hat)

Please have a look at this sequence:

Mark in yellow every 10th integer:

Erase all yellow terms:

If you concatenate the result (omit the blanks), you’ll get the starting sequence:

E=S=

The nice thing being that the succession of all yellow terms form also the starting sequence:

Y=E=S=

. . . . . . . . . 1 . . . . . . . . . 2 . . . . . . . . . 3 . . . . . . . . . 4 . . . . . . . . . 5 . . . . . . . . . 6 . . . . . . . . . 7 . . . . . . . . . 8 . . . . . . . . . 9 . . . . . . . . . 1 . . . . . . . . . 1 . . . . . . . . . 1 . . . . . . . . . 1 . . . . . . . . . 1 . . . . . . . . . 1 . . . . . . . . . 1 . . . . . . . . . 1 . . . . . . ...

Could such sequences be called «super-fractals»?

----------

There are infinitely many decimation-like sequences: instead of [1,2,3,4,5,6,7,8,9] the first nine integers could have been [7,15,8933,42,3001,8,666,0,666], for instance (with or without repeted terms). This new set would have produced this 10-super-fractal:

7 15 8933 42 3001 8 666 0 666 7 7 7 7 7 7 7 7 7 7 15 7 15 7 15 7 15 7 15 7 8933 15 7 8933 15 7 8933 15 7 8933 42 15 7 8933 42 15 7 8933 42 15 3001 7 8933 42 15 3001 7 8933 42 15 8 3001 7 8933 42 15 8 3001 7 8933 666 42 15 8 3001 7 8933 666 42 15 0 8 3001 7 8933 666 42 15 0 8 666 3001 7 8933 666 42 15 0 8 666 7 3001 7 8933 666 42 15 0 8 666 7 7 3001 7 8933 666 42 15 0 8 7 666 7 7 3001 7 8933 666 42 15 7 0 8 7 666 7 7 3001 7 8933 7 666 42 15 7 0 8 7 666 7 7 7 3001 7 8933 7 666 42 15 7 7 0 8 7 666 7 7 7 3001 7 7 8933 7 666 42 15 7 ...

----------

Instead of yellowing every 10th integer, one could mark every 7th, or 215th, or 3rd term, etc. – producing thus another infinite bunch of super-fractals; here is such a super-fractal with every 6th term marked:

1 2 3 4 5 1 1 1 1 1 1 2 1 2 1 2 1 3 2 1 3 2 1 4 3 2 1 4 3 5 2 1 4 3 5 1 2 1 4 3 5 1 1 2 1 4 3 1 5 1 1 2 1 1 4 ...

----------

The lowest bound (for the interval between two yellow marks) seems to be 2; integers 0 et 1 would then produce (a):

(a) 0,1,0,0,0,1,0,1,0,0,1,0,0,0,0,1,0,1,0,0,0,0,1,1,0,1,0,0,0,0,0,0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,...

Let’s check if it works:

1) mark every 3rd integer of (a) in yellow and get (b):

(a) 0,1,0,0,0,1,0,1,0,0,1,0,0,0,0,1,0,1,0,0,0,0,1,1,0,1,0,0,0,0,0,0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,...

(b) 0,1,0,0,0,1,0,1,0,0,1,0,0,0,0,1,0,1,0,0,0,0,1,1,0,1,0,0,0,0,0,0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,...

2) erase all yellow marks from (b) and get (c):

(b) 0,1,0,0,0,1,0,1,0,0,1,0,0,0,0,1,0,1,0,0,0,0,1,1,0,1,0,0,0,0,0,0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,...

3) concatenate all terms of (c) and get (d):

(d) 0,1,0,0,0,1,0,1,0,0,1,0,0,0,0,1,0,1,0,0,0,0,1,1,0,1,0,0,0,0,0,0,...

4) compare (d) to the starting sequence (a):

(a) 0,1,0,0,0,1,0,1,0,0,1,0,0,0,0,1,0,1,0,0,0,0,1,1,0,1,0,0,0,0,0,0,0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,...

(d) 0,1,0,0,0,1,0,1,0,0,1,0,0,0,0,1,0,1,0,0,0,0,1,1,0,1,0,0,0,0,0,0,...

... same sequences!

5) write down the successive previously yellow marked (and erased) terms from (b) and get (e):

(b) 0,1,0,0,0,1,0,1,0,0,1,0,0,0,0,1,0,1,0,0,0,0,1,1,0,1,0,0,0,0,0,0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,...

(e) 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, ...

6) concatenate all terms of (e) and get (f):

(e) 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, ...

(f) 0,1,0,0,0,1,0,1,0,0,1,0,0,0,0,1, ...

7) Compare (f) to the starting sequence (a):

(a) 0,1,0,0,0,1,0,1,0,0,1,0,0,0,0,1,0,1,0,0,0,0,1,1,0,1,0,0,0,0,0,0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,...

(f) 0,1,0,0,0,1,0,1,0,0,1,0,0,0,0,1, ...

... same sequences again!

Isn’t this (a) sequence the mother of all decimation-like super-fractals?

(a) is not in the OEIS (it is now as A117943). Nor is (g) where all 0’s and 1’s of (a) have been switched:

(g) 1,0,1,1,1,0,1,0,1,1,0,1,1,1,1,0,1,0,1,1,1,1,0,0,1,0,1,1,1,1,1,1,0,0,0,1,1,0,1,1,1,1,1,1,1,1,1,0,...

What could be the law ruling the distribution of 0’s and 1’s in (a)? Gilles Sadowski has computed the first 1000 terms of (a) :

(a)=

0 1 0 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 0 0 0 0 1 1 0 1 0 0 0 0 0 0 1 1 1 0 0 1 0 0 0 0 0 0 0 0 0 1 1 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 1 1 0 0 1 1 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 1 1 1 0 1 1 0 0 0 1 1 1 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 1 1 0 0 0 1 0 1 0 1 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 0 1 0 0 1 0 0 1 1 0 1 1 1 1 0 0 1 1 0 1 0 1 1 0 0 0 1 0 1 0 0 1 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 1 0 0 1 1 0 1 1 1 0 0 0 1 1 1 1 1 1 0 0 1 0 0 0 0 1 0 1 0 1 1 1 0 1 1 1 0 1 1 0 0 0 1 1 1 0 0 1 0 0 1 0 1 0 0 0 0 1 1 0 0 1 0 0 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 0 1 1 1 1 1 1 0 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1 0 1 0 0 1 1 1 1 1 0 1 0 1 1 0 0 1 0 1 0 0 0 0 1 1 1 0 1 0 0 0 1 0 0 0 0 1 0 0 1 0 0 0 0 1 0 1 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 0 0 1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 1 0 0 1 0 0 0 1 0 1 1 1 1 0 0 0 1 0 1 1 0 0 1 1 1 1 0 1 0 0 1 0 0 1 1 0 1 1 1 1 0 0 1 1 0 1 0 0 0 1 1 1 1 1 1 0 1 1 0 0 1 0 1 0 1 0 0 0 0 1 1 0 1 0 0 0 0 0 0 1 1 1 0 0 1 0 0 0 1 1 1 0 1 1 1 1 0 0 1 0 0 1 1 0 0 0 0 1 0 0 1 0 0 0 0 1 0 1 0 1 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 1 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 1 0 0 1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 1 0 1 1 1 0 1 1 0 1 1 1 0 1 ...

What else can be said about decimation-like sequences and/or super-fractals?

Here is the building method used for the 10-super-fractal which opens this page:

1) choose de decimation-step d (here d=10 --> we will cancel all terms whose index is a multiple of 10)

2) choose (d-1) integers at random (they will form the starting "seed" --> here 1,2,3,4,5,6,7,8,9)

3) draw line (1):

(1) .........X.........X.........X.........X.........X.........X...

[this line (1) alternates 9 empty simple boxes and 1 "super-box" : a dot (.) stands for a simple box, an "X" for a super-box]

4) draw the "punched" line (2) under line (1):

(1) .........X.........X.........X.........X.........X.........X...

(2) ......... ......... ......... ......... ......... ......... ...

(this line is the same as the previous one -- but *without* the "X" super-boxes)

5) draw the continuous (S) line, which will be the "sum" of lines (1) and (2):

(1) .........X.........X.........X.........X.........X.........X...

(2) ......... ......... ......... ......... ......... ......... ...

(S) ...............................................................

6) Fill the first 9 empty single boxes of (2) with the chosen "seed" :

(1) .........X.........X.........X.........X.........X.........X...

(2) 123456789 ......... ......... ......... ......... ......... ...

(S) ...............................................................

Those 9 integers are also the first 9 X’s:

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 ......... ......... ......... ......... ......... ...

(S) ...............................................................

Start to "sum" (1) and (2) [to "sum" is to "push" (1) into (2) which gives S]:

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 ......... ......... ......... ......... ......... ...

(S) 1234567891.....................................................

Now comes the construction trick: line (2) must always be filled by copying S’s succession of integers, *but* one can never write *under* the "X’s". So we will write, to the right of the last 9 of (2), the "1" which ends S for the moment:

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 1........ ......... ......... ......... ......... ...

(S) 1234567891.....................................................

We see now that the succession of terms in (2) is the same as the succession of terms in S [this is because we cannot use for writing purpose the "hole" which is under the "1" of (1)]

We "sum" again:

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 1........ ......... ......... ......... ......... ...

(S) 12345678911....................................................

The last "1" which appears on line S forces the writing of a corresponding "1" behind the final "1" of line (2) -- because line (2) always copies with a little delay the succession of terms in S:

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 11....... ......... ......... ......... ......... ...

(S) 12345678911....................................................

We "sum":

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 11....... ......... ......... ......... ......... ...

(S) 123456789111...................................................

We copy S in (2):

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111...... ......... ......... ......... ......... ...

(S) 123456789111...................................................

We "sum":

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111...... ......... ......... ......... ......... ...

(S) 1234567891111..................................................

We copy S in (2):

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 1111..... ......... ......... ......... ......... ...

(S) 1234567891111..................................................

... and so on -- till:

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 ......... ......... ......... ......... ...

(S) 123456789111111111.............................................

We "sum":

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 ......... ......... ......... ......... ...

(S) 1234567891111111111............................................

We copy S in (2):

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 1........ ......... ......... ......... ...

(S) 1234567891111111111............................................

We "sum":

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 1........ ......... ......... ......... ...

(S) 123456789111111111121..........................................

We copy the last *2* integers of S in (2):

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 121...... ......... ......... ......... ...

(S) 123456789111111111121..........................................

We "sum":

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 121...... ......... ......... ......... ...

(S) 12345678911111111112121........................................

We copy the last *2* integers of S in (2):

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 12121.... ......... ......... ......... ...

(S) 12345678911111111112121........................................

We "sum" and copy till:

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 121212121 21....... ......... ......... ...

(S) 12345678911111111112121212121..................................

We "sum" again:

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 121212121 21....... ......... ......... ...

(S) 12345678911111111112121212121321...............................

We copy the last *3* integers of S in (2):

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 121212121 21312.... ......... ......... ...

(S) 12345678911111111112121212121321...............................

We "sum" and copy, till:

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 121212121 213213213 21....... ......... ...

(S) 12345678911111111112121212121321321321.........................

We "sum":

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 121212121 213213213 21....... ......... ...

(S) 123456789111111111121212121213213213213421.....................

We copy the last *4* integers of S in (2):

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 121212121 213213213 213421... ......... ...

(S) 123456789111111111121212121213213213213421.....................

We "sum" and copy, till:

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 121212121 213213213 213421342 1........ ...

(S) 1234567891111111111212121212132132132134213421.................

We "sum" again:

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 121212121 213213213 213421342 1........ ...

(S) 123456789111111111121212121213213213213421342134251............

We copy the last *5* integers of S in (2):

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 121212121 213213213 213421342 134251... ...

(S) 123456789111111111121212121213213213213421342134251............

We "sum" and copy till:

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 121212121 213213213 213421342 134251342 51.

(S) 12345678911111111112121212121321321321342134213425134251.......

We "sum" again:

(1) .........1.........2.........3.........4.........5.........6...

(2) 123456789 111111111 121212121 213213213 213421342 134251342 51.

(S) 12345678911111111112121212121321321321342134213425134251342651.

... etc. This should be clear now : line S is the sequence we were looking for.

[One must *not* forget that line (1) builds up step by step too: line (1) is also a copy of S! Thus after the "seed" 1,2,3,4,5,6,7,8,9 the next "X" value is *not* 10 but 1! (because the 10th term of S is "1")]

We then get at the end (terms computed by Gilles Sadowski):

1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 1 2 1 2 1 2 1 2 1 3 2 1 3 2 1 3 2 1 3 4 2 1 3 4 2 1 3 4 2 5 1 3 4 2 5 1 3 4 2 6 5 1 3 4 2 6 5 1 3 7 4 2 6 5 1 3 7 4 2 8 6 5 1 3 7 4 2 8 6 9 5 1 3 7 4 2 8 6 9 1 5 1 3 7 4 2 8 6 9 1 1 5 1 3 7 4 2 8 6 1 9 1 1 5 1 3 7 4 2 1 8 6 1 9 1 1 5 1 3 1 7 4 2 1 8 6 1 9 1 1 1 5 1 3 1 7 4 2 1 1 8 6 1 9 1 1 1 5 1 1 3 1 7 4 2 1 1 8 6 1 1 9 1 1 1 5 1 1 3 1 1 7 4 2 1 1 8 6 1 2 1 9 1 1 1 5 1 1 3 1 1 1 7 4 2 1 1 8 6 2 1 2 1 9 1 1 1 5 1 1 1 3 1 1 1 7 4 2 1 2 1 8 6 2 1 2 1 9 1 1 1 1 5 1 1 1 3 1 1 2 1 7 4 2 1 2 1 8 6 1 2 1 2 1 9 1 1 1 1 2 5 1 1 1 3 1 1 2 1 1 7 4 2 1 2 1 8 6 1 3 2 1 2 1 9 1 1 1 1 2 2 5 1 1 1 3 1 1 2 1 1 1 7 4 2 1 2 1 8 3 6 1 3 2 1 2 1 9 1 2 1 1 1 2 2 5 1 1 1 1 3 1 1 2 1 1 1 7 4 3 2 1 2 1 8 3 6 1 3 2 2 1 2 1 9 1 2 1 1 1 1 2 2 5 1 1 1 1 3 3 1 1 2 1 1 1 7 4 3 4 2 1 2 1 8 3 6 1 3 2 2 2 1 2 1 9 1 2 1 1 1 1 1 2 2 5 1 1 1 3 1 3 3 1 1 2 1 1 1 4 7 4 3 4 2 1 2 1 8 2 3 6 1 3 2 2 2 1 2 1 1 9 1 2 1 1 1 1 1 3 2 2 5 1 1 1 3 1 3 4 3 1 1 2 1 1 1 4 7 2 4 3 4 2 1 2 1 8 2 5 3 6 1 3 2 2 2 1 2 1 1 1 9 1 2 1 1 1 1 3 1 3 2 2 5 1 1 1 3 4 1 3 4 3 1 1 2 1 1 2 1 4 7 2 4 3 4 2 1 5 2 1 8 2 5 3 6 1 3 1 2 2 2 1 2 1 1 1 9 3 1 2 1 1 1 1 3 1 3 4 2 2 5 1 1 1 3 4 1 2 3 4 3 1 1 2 1 1 2 6 1 4 7 2 4 3 4 2 1 5 5 2 1 8 2 5 3 6 1 1 3 1 2 2 2 1 2 1 1 3 1 9 3 1 2 1 1 1 1 4 3 1 3 4 2 2 5 1 1 2 1 3 4 1 2 3 4 3 1 6 1 2 1 1 2 6 1 4 7 5 2 4 3 4 2 1 5 5 2 1 1 8 2 5 3 6 1 1 3 3 1 2 2 2 1 2 1 1 3 7 1 9 3 1 2 1 1 1 1 4 4 3 1 3 4 2 2 5 1 2 1 2 1 3 4 1 2 3 4 6 3 1 6 1 2 1 1 2 6 5 1 4 7 5 2 4 3 4 2 1 1 5 5 2 1 1 8 2 5 3 3 6 1 1 3 3 1 2 2 7 2 1 2 1 1 3 7 1 9 4 3 1 2 1 1 1 1 4 4 2 3 1 3 4 2 2 5 1 2 8 1 2 1 3 4 1 2 3 4 6 6 3 1 6 1 2 1 1 2 5 6 5 1 4 7 5 2 4 3 1 4 2 1 1 5 5 2 1 1 3 8 2 5 3 3 6 1 1 3 7 3 1 2 2 7 2 1 2 1 4 1 3 7 1 9 4 3 1 2 2 1 1 1 1 4 4 2 3 1 8 3 4 2 2 5 1 2 8 1 6 2 1 3 4 1 2 3 4 6 9 6 3 1 6 1 2 1 1 2 5 5 6 5 1 4 7 5 2 4 1 3 1 4 2 1 1 5 5 2 3 1 1 3 8 2 5 3 3 6 7 1 1 3 7 3 1 2 2 7 4 2 1 2 1 4 1 3 7 1 2 9 4 3 1 2 2 1 1 1 8 1 4 4 2 3 1 8 3 4 6 2 2 5 1 2 8 1 6 2 9 1 3 4 1 2 3 4 6 9 1 ...

The (simple) algorithm used says:

a) put the seed at the beginning of (2)

b) copy the seed in the successive X’s of line (1)

c) "Sum"

d) copy the "sum" so far in the proper empty boxes of (2) and (1)

e) loop in (c)

This produces the three "equivalent" lines (1), (2) and S.

____________________

This e-mail (in french), was sent to me by Jacques Tramu on May 1^st, 2006 :

Je suis en train de regarder combien il faut en moyenne d’itérations pour calculer le n^e terme pour n allant de 10 à 10**100 (1 googol).

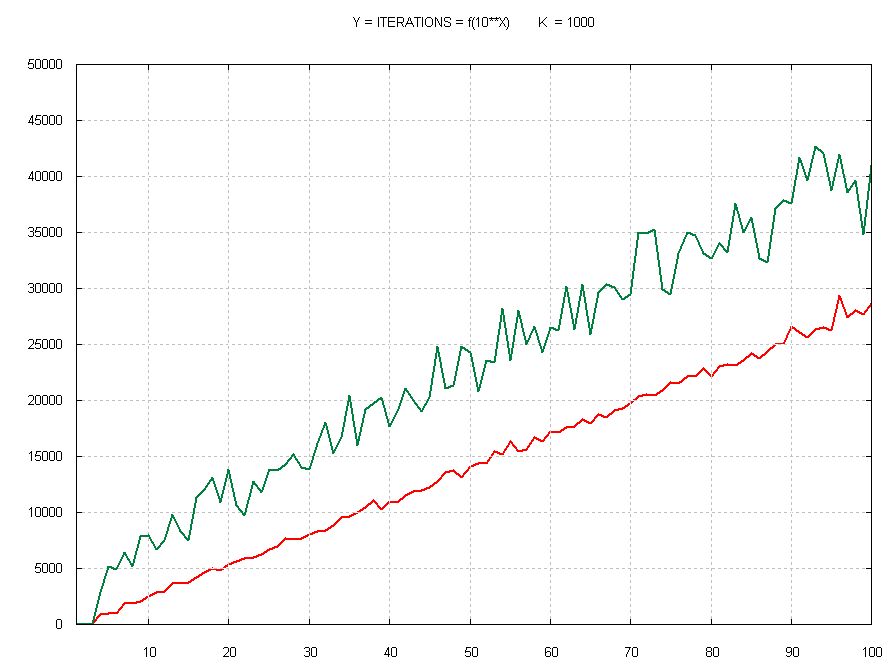
Voir la courbe ci-joint pour k = 1000. C’est remarquablement linéaire [en abscisse, log10(n) ; en vert le nombre max d’itérations].

Éric : pour k = 10, voici le 100.........0000000^e terme (cent zéros), et les 10 suivants :

1 2 1 1 1 7 2 1 1 7 7

à suivre.

J.T.

____________________

This e-mail was sent to me the same day by Kerry Mitchell :

Hi Eric,

I’ve been playing with your decimation sequences--very interesting!

Attached is an image I created to simultaneously show a 2-integer, a 3-integer, and a 4-integer sequence.

Each of the 576 (24 x 24) squares is one of 24 symbols for the 2 x 3 x 4 = 24 possible values of the 3 sequences.

Kerry

Beautiful, Kerry, thanks !

___________________

Note of May 10th, 2006

I’ve noticed yesterday that more super-fractals can be created by increasing the size of the « X » super-boxes (see above). Here is an example for a super-box of size 3 which follows an empty 2-single box:

(1) ..010..100..110..000..110..110..000..011..000..110..110..

(2) 01 01 00 11 00 00 11 01 10 00 00 11

(S) 010100110000110110000011000110110000101110000001100011011...

So S must be understood like this:

0,1,0,1,0,0,1,1,0,0,0,0,1,1,0,1,1,0,0,0,0,0,1,1,0,0,0,1,1,0,1,1,0,0,0,0,1,0,1,1,1,0,0,0,0,0,0,1,1,0,0,0,1,1,0,1,1,...

«Keep two integers, underline the next three; keep two integers again, underline the next three; keep two again, underline three; etc. The concatenation of all kept integers is the sequence itself – and so is the concatenation of all underlined integers, too»

S could be seen as a «keep 2/underline 3» sequence. Here is a «keep 3/underline 2» sequence:

(1) ...01...20...10...10...20...10...21...00...10...10...21...

(2) 012 010 102 010 210 010 102 102 001 010 102 211

(S) 0120101020102100101021020010101022110200001100101010221211...

0,1,2,0,1,0,1,0,2,0,1,0,2,1,0,0,1,0,1,0,2,1,0,2,0,0,1,0,1,0,1,0,2,2,1,1,0,2,0,0,0,0,1,1,0,0,1,0,1,0,1,0,2,2,1,2,1,1,...

[So A117943, the «mother of all super-fractals», is simply a «keep 2/underline 1» sequence; and the decimation sequence which opens this page a «keep 9/underline 1» sequence]

To build such super-fractal sequences, one must always start with at least a «keep 2» statement; any «keep 1» statement (no matter how much integers are underlined) would produce this kind of rather dull sequence:

(1) .0000.0000.0000.0000.0000.0000.0000.0000.0000.0000.0000.0000

(2) 0 0 0 0 0 0 0 0 0 0 0 0

(S) 000000000000000000000000000000000000000000000000000000000000...

To avoid more dull sequences, k (number of kept integers) and u (number of underlined integers) must be mutually prime [k must not divide u and u must not divide k (except if u=1, of course)].

If one starts a sequence with a «keep 2» statement, the sequence will contain only two different types of integers (0’s and 1’s; or 1’s and 0’s; or 17’s and 9’s ; etc.) A «keep 3» statement will thus produce a sequence showing only three different integers (no matter how much is underlined). So, if you want a sequence containing all 26 letters of the alphabet, you’ll have to start with a «keep 26» statement.

The values k and u can vary, of course, inside a sequence itself; one only needs a simple rule to clearly see what is kept and what is underlined. Here is a prime-based super-fractal:

(1) ..010.....1001001...........1001001001100.................

(2) 01 01001 00110010010 01100100101001001

(S) 0101001001100100100110010010100100100110001100100101001001

S must be understood like this:

0,1,0,1,0,0,1,0,0,1,1,0,0,1,0,0,1,0,0,1,1,0,0,1,0,0,1,0,1,0,0,1,0,0,1,0,0,1,1,0,0,0,1,1,0,0,1,0,0,1,0,1,0,0,1,0,0,1,...

«Keep 2 integers, underline 3, keep 5, underline 7, keep 11, underline 13, keep 17... etc. The concatenation of all kept integers is the sequence itself; the concatenation of all underlined integers is the sequence itself too»

Here is a fractal-sequence where the keep/underline rule is given by the sequence itself (a self-describing super-fractal?):

(1) ..2..12..2..21.22..12..2.22..11..2..22..21.22..2..2.12..22..1

(2) 21 22 21 22 1 22 22 1 12 22 21 22 2 21 22 1 21 12

(S) 2122212212222112222122221221211222212221212222122221122122121

It reads: keep 2 integers,

underline 1,

keep 2,

underline 2,

keep 2,

underline 1,

keep 2,

underline 2,

keep 1,

underline 2,

keep 2,

underline 2,

keep 2,

underline 1,

keep 1, etc.

The diagonal is the sequence itself (sequence coming soon in the OEIS, I hope). Again, the concatenation of all kept integers is the sequence itself – and so is the concatenation of all underlined integers.

Another self-describing super-fractal, with a different «seed» (2,3 instead of 2,1):

(1) ..232..322..33...222..23..33...322...222..22..32..33..333

(2) 23 23 22 332 22 23 333 222 22 22 32 33

(S) 232322332222333322222223233333332222222222222232323333333...

It reads: keep 2 integers,

underline 3,

keep 2,

underline 3,

keep 2,

underline 2,

keep 3,

underline 3,

keep 2,

underline 2,

keep 2,

underline 2,

keep 3,

underline 3,

keep 3, etc.

A last remark: as many readers have already guessed, it is possible to build multi-layered fractal-sequences; one could keep, underline and italicise different integers; here is an example where keep=2, underline=3 and italicise=4:

ital(i) .....0101.....0010.....1011.....0000.....1000.....1011.....

undl(u) ..010 ..100 ..101 ..011 ..000 ..010 ..001

keep(k) 01 01 00 10 10 11 00

seq.(S) 01010010101100001000101101110011000010000100011010101100001...

S (painfully) reads:

0,1,0,1,0,0,1,0,1,0,1,1,0,0,0,0,1,0,0,0,1,0,1,1,0,1,1,1,0,0,1,1,0,0,0,0,1,0,0,0,0,1,0,0,0,1,1,0,1,0,1,0,1,1,0,0,0,0,1,...

a) keep the first 2 integers, ignore the next 7, keep the next 2 integers, ignore the next 7, etc. The concatenation of all kept integers is the sequence itself;

b) underline integers # 3,4 and 5; ignore the next 6, underline the next 3, ignore the next 6, underline the next 3, etc. The concatenation of all underlined integers is the sequence itself;

c) ignore the first 5 integers, italicise the next 4, ignore the next 5 integers, italicise the next 4, etc. The concatenation of all italicised integers is the sequence itself... Ouf!

Best,

É.

_________

A warm thanks to those who helped so far – and especially to Gilles Sadowski, Nicolas Graner and Gilles Esposito-Farèse !

Please find here the .pdf paper of Jean-Paul Delahaye about this very subject, which was published in march 2007 in the french magazine « Pour la Science ».

__________

Back to main page, here

__________

BREAKING NEWS — got this e-mail yesterday [September 21st, 2010] from Jean-Marc Falcoz:

Salut Eric,

J’ai découvert (très tardivement :o)) tes magnifiques suites du lézard ! Une fois de plus bravo.

J’enseigne les maths appliquées à des bons élèves de 18-20 ans, alors j’ai fait un petit cours de deux heures avec ces suites. On utilise Mathematica, et les élèves ont trouvé ça "très cool" (c’est l’expression qu’ils ont employée !)

On a un peu regardé à droite et à gauche en regardant les trajectoires associées, et en changeant des paramètres – enfin bref, on s’est bien amusés.

Merci à toi.

En PJ, les 3 pages d’introduction que je leur ai données.

Amicalement.

Suites du lézard et suites de décimation

Une suite du lézard est une suite possédant deux propriétés étonnantes :

Quand on ôte un terme sur trois de la suite, on retrouve la même suite.

Les termes restants reforment également la suite d’origine.

Prenons par exemple 0, 1 comme premiers termes :

L = 0,1,0,0,0,1,0,1,0,0,1,0,0,0,0,1,0,1,0,0,0,0,1,1,0,1,0,0,0,0,0,0,1,1,1,0,...

Afin de mieux visualiser la suite, on peut envisager l’accumulation de tous les termes précédents:

L2 = 0,1,1,1,1,2,2,3,3,3,4,4,4,4,4,5,5,6,6,6,6,6,...

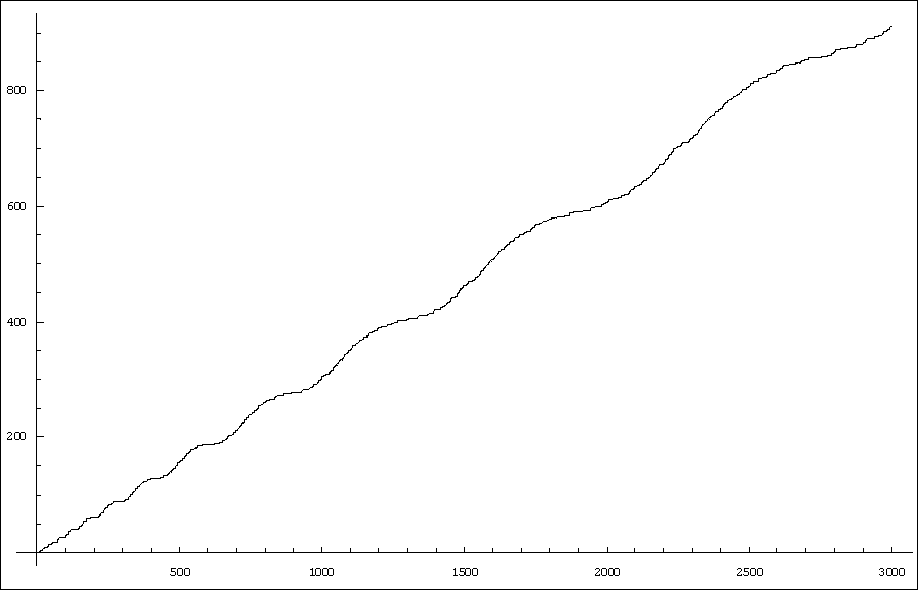
Les suites du lézard tirent leur nom du fait que si on arrache la queue d’un lézard (donc un tiers de la bestiole), la queue repousse et on retrouve le lézard.

Le petit programme que je vous fournis construit les termes de la suite commençant par 0,1,... et représente également l’accumulation des termes, puis cherche les positions des séquences comportant 23 fois de suite le terme « 0 ».

Prenez le temps de comprendre son fonctionnement et de changer quelques paramètres.

Que représente la pente de la droite linéaire (non dessinée) qui traverse toutes les ondulations ?

Quelle est la pente de cette droite ?

Combien de suites du lézard essentiellement différentes a-t-on ?

« Les Romains pratiquaient la décimation lors des défaites de leurs propres armées. En cas de défaite grave, la sentence pouvait être cruelle : un légionnaire sur dix était exécuté parmi les survivants, l’objectif étant de punir la légion, qui était jugée collectivement responsable de la défaite. Les légionnaires devant être punis étaient divisés en groupes de dix. Chaque soldat piochait un « papier », et ceux sur qui le sort tombait étaient battus à mort ou lapidés par leurs neuf camarades. » (tiré de Wikipédia)

Sur le même principe qu’une suite du lézard, pour obtenir une suite de décimation, on cherche à retrouver la suite d’origine en enlevant un terme sur dix, la suite des termes ôtés redonnant elle aussi la suite originale.

D = 1,2,3,4,5,6,7,8,9,1,1,1,1,1,1,1,1,1,1,2,1,2,1,2,1,2,1,2,1,3,2,1,3,2,1,3,2,1,3,4,2,...

En vous inspirant du programme précédent, créez la fonction f [t_ , nbtermes_] donnant nbtermes termes de la suite de décimation généralisée dont les premiers éléments sont dans la liste t.

Par exemple f[{1,2,3,4,5,6,7,8,9},10000] donnera les 10000 premiers termes de la suite commençant par 1,2,3,4,5,6,7,8,9.

On aura donc :

f[{1,2,3,4,5,6,7,8,9},10000] = 1,2,3,4,5,6,7,8,9,1,1,1,1,1,1,1,1,1,1,2,1,2,1,2,1, ...

Ou encore

f[{1,2,3,4},400] qui donnera 1,2,3,4,1,1,1,1,1,2,1,2,1,2,3,1,2,3,1,4, ...

Comme précédemment, représenter graphiquement l’accumulation des termes, puis trouver les positions (si elles existent) des séquences « 555 » (par exemple), ou encore « 666 » dans une suite de décimation. Et enfin, faire une table des fréquences du nombre de 1, de 2, de 3, ... contenus dans la suite.

Pour les 10000 premiers termes de la suite de décimation, vous devriez trouver environ 29% de « 1 », 19% de « 2 », 14% de « 3 », ...

Expérimentez, par exemple en assignant une direction à chaque terme de la suite, puis en représentant la trajectoire en découlant (ci-dessous 300 termes de la suite commençant par 1,2,3,4,5,6,7,8,9,1,1,... donc la suite de décimation, et 400 termes de celle commençant par 1,2,3,4,1,1,1,1,1,2,1,2... avec un terme sur cinq.

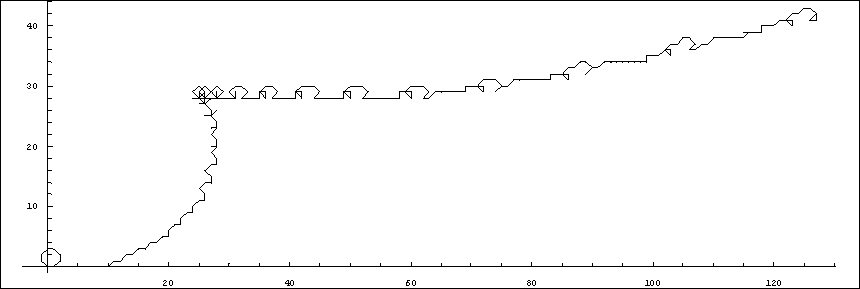
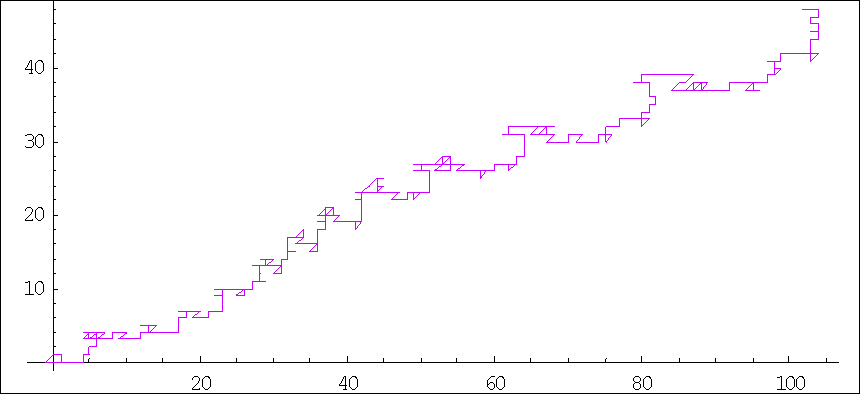
À vous de jouer...

Qu’obtient-on pour une suite de « quadrimation », ou une de « quintimation » commençant par 1,2,3, ... ?

Ci-dessous, la trajectoire associée aux 10 000 premiers termes de la suite de décimation, en modifiant légèrement la règle de formation de la trajectoire ; on constate que le 1 est plus fréquent dans les termes de la suite que le 2, qui est lui-même plus fréquent que le 3, et ainsi de suite.

En guise de « compensation directionnelle » on multiplie par 2 la direction associée au terme 2, de même, on multiplie par 3 celle associée au terme 3, ... et, finalement, la direction associée à 9 est multipliée par 9.

On obtient alors une jolie et curieuse amorce de spirale.

Le principe de ces suites est dû à Eric Angelini, et elles ont été présentées dans le magazine « Pour La Science »