Le dernier chiffre plus 1

Hello Seqfans,

This was fun to imagine:

Start S with a(n)=1

Now a(n+1) is always the smallest integer not yet present in S such

that a(n+1) is a multiple of (d+1), d being the last digit of a(n):

S=1,2,3,4,5,6,7,8,9,10,11,12,15,18,27,16,14,20,13,24,25,30,17,32,21,...

S is a permutation of N(aturals), I hope (it was imagined with this

purpose in mind).

Example:

2 is the smallest integer not yet in S that is a multiple of (1+1)

3 is the smallest integer not yet in S that is a multiple of (2+1)

4 is the smallest integer not yet in S that is a multiple of (3+1)

...

10 is the smallest integer not yet in S that is a multiple of (9+1)

11 is the smallest integer not yet in S that is a multiple of (0+1)

12 is the smallest integer not yet in S that is a multiple of (1+1)

15 is the smallest integer not yet in S that is a multiple of (2+1)

18 is the smallest integer not yet in S that is a multiple of (5+1)

27 is the smallest integer not yet in S that is a multiple of (8+1)

16 is the smallest integer not yet in S that is a multiple of (7+1)

... |

This is d, the last digit of a(n) -----------------------------+

I’d like to see the graph of S... Any taker?

Best,

É.

__________

Emmanuel Vantieghem was quick to answer:

> Concerns : your mail to the SeqFans of 4/12/2013

> Attached  : a small plot of the first 1024 elements of S

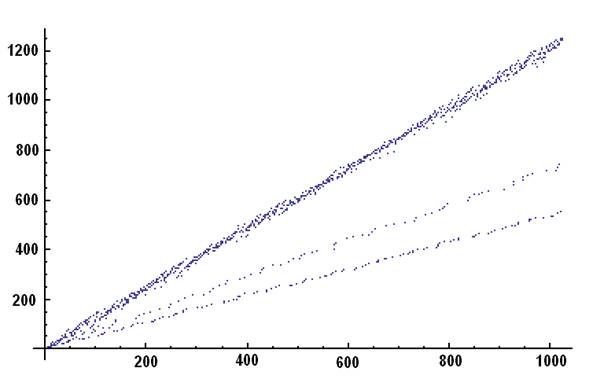
Many thanks, Emmanuel!

Best,

É.