Any 2 neighboring digits

sum to a prime

Hello SeqFans,

Any digit-pair in S sums to a prime, commas or not:

S is supposed not to show twice the same integer, and S wants to be the lexico-first such seq.

----------

The same seq with prime absolute differences between two neighboring digits is perhaps T:

Best,

É.

__________

[Lars Blomberg] :

Hello Eric,

S = 1, 2, 3, 4, 7, 6, 5, 8, 9, 20, 21, 11, 12, 14, 16, 50, 23, 25, 29, 41, 43, 47, 49, 83, 85, 61, 65, 67, 411, 111, 112, 30, 32, 34, 38, 52, 56, 58, 92, 94, 70, 74, 76, 114, 98, 302, 116, 120, 202, 121, 123, 89, 203, 205, 207, 412, 125, 211, 129, 212, 141, 143, 214, 147, 414, 149, 216, 161, 165, 230, 232, 167, 416, 502, 303, 234, 305, 238, 307, 430, 250, 252, 320, 256, 503, 258, 321, 292, 323, 294, 325, 298, 329, 432, 341, 434, 343, 438, 347, 470, 349, 474, 383, 476, 505, 611, 492, 385, 612, 389, 494, 702, 507, 498, 520, 521, 614, 703, 830, 523, 832, 525, 616, 529, 834, 705, 650, 561, 652, 565, 656, 567, 658, 583, 838, 585, 670, 589, 850, 707, 674, 741, 676, 743, 852, 920, 747, 4111, 1111, 1112, 921, 1114, 749, 856, 761, 1116, 765, 858, 923, 892, 925, 894, 767, 4112, 929, 898, 941, 1120, 2020, 2021, 1121, 1123, 2023, 2025, 2029, 2030, 2032, 943, 2034, 947, 4114, 949, 2038, 983, 2050, 2052, 985, 2056, 1125, 2058, 989, 2070, 2074, 1129, 2076, 1141, 1143, 2111, 1147, 4116,...

Here is a graph of S with values < 10^5.

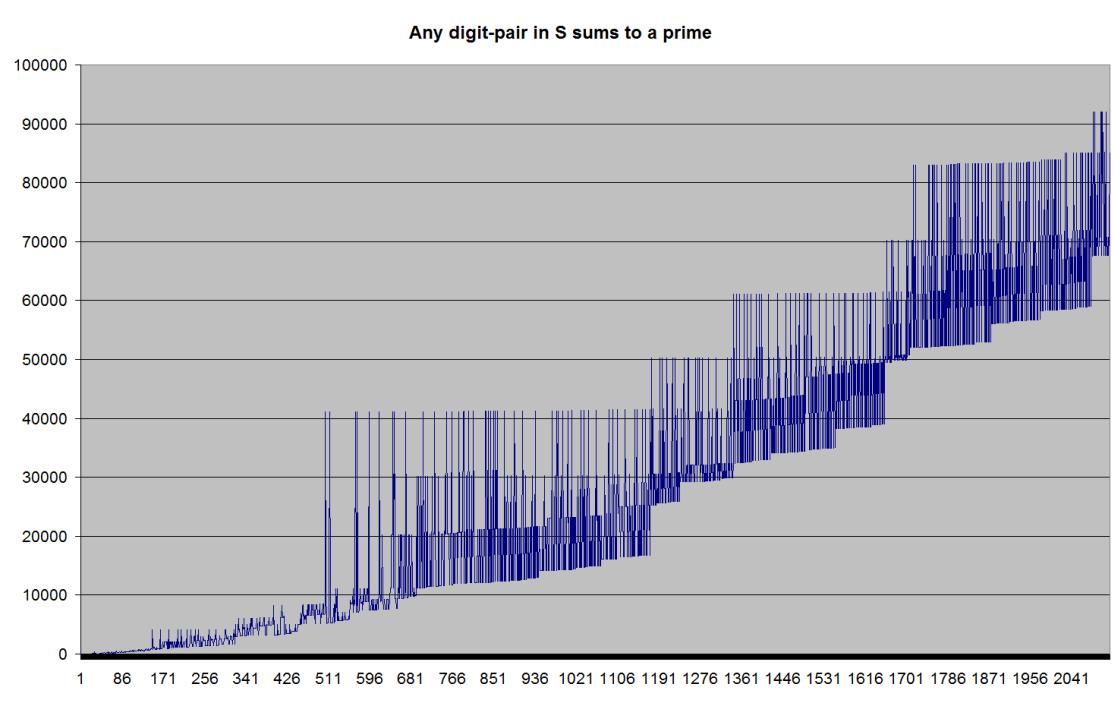
S_sums_to_prime

For each maximum value 10^n there are much fewer candidates that are internally consistent.

Calculating the candidates first greatly reduces the work of finding the sequence,

This table shows the length of the sequence and the number of candidates for some maximum values

Max = 10^n Sequence Candidates

2 28 41

3 147 166

4 503 643

5 2119 2467

6 7581 9432

7 30731 36078

8 112977 137844

9 447183 527115

A little on the side: The number of candidates increases by a factor of about 3.82 for each power of 10.

The T sequence has similar properties, although the factor between the candidates is about 4.64.

[The T seq has prime absolute differences between two neighboring digits]:

T = 1, 3, 5, 2, 4, 6, 8, 13, 14, 7, 9, 20, 24, 16, 18, 30, 25, 27, 29, 41, 31, 35, 36, 38, 50, 52, 42, 46, 47, 49, 61, 63, 53, 57, 58, 64, 68, 69, 70, 72, 74, 75, 79, 202, 92, 94, 96, 81, 83, 85, 86, 97, 203, 130, 205, 207, 241, 302, 413, 131, 303, 135, 242, 414, 136, 138, 141, 305, 246, 142, 416, 146, 147, 247, 249, 250, 252, 418, 149, 253, 161, 307, 257, 258, 163, 164, 168, 169, 270, 272, 420, 274, 181, 313, 183, 185, 275, 279, 292, 424, 186, 314, 294, 296, 316, 318, 350, 297, 425, 352, 427, 429, 461, 353, 502, 463, 503, 505, 357, 464, 613, 507, 468, 358, 361, 363, 520, 364, 614, 616, 368, 369, 469, 470, 381, 383, 524, 618, 385, 386, 472, 474, 630, 525, 702, 475, 703, 527, 479, 492, 494, 631, 496, 497, 529, 635, 705, 707, 530, 531, 636, 813, 535, 720, 536, 814, 638, 538, 570, 572, 574, 641, 642, 575, 724, 646, 816, 818, 579, 647, 581, 649, 681, 683, 583, 585, 725, 727, 586, 830, 729, 685, 741, 686, 831, 692, 742, 746, 835, 747,...

One can think of many other properties of 2 digits, such as the sum is divisible by 3 and many other that will lead to different sequences, which I am sure you are already aware of. Do you think it would be useful to investigate those?

Regards,

Lars.

__________

[Maximilian Hasler]:

> Eric Angelini wrote:

> Any digit-pair in S sums to a prime, commas or not:

> S=1,2,3,4,7,6,5,8,9,20,21,11,12,14,16,50,23,25,29,41,43,47,49,83,85,61,65,

I think "any 2 subsequent digits" would be better, "any pair" does not require that they are neighbors.

> S is supposed not to show twice the same integer, and S wants to be the lexico-first such seq.

The sequence

0, 2, 1, 4, 3, 8, 5, 6, 7, 41, 11, 12, 9, 20, 21, 14, 16, 50, 23, ...

has the same property and is lexicographically smaller than yours. ;-)

My script

EA114(n,a=[1],u=0)={ while(#a<n, u+=1<<a[#a];

for(t=a[1]+1,9e9, bittest(u,t) & next; my(d=concat(a[#a]%10,digits(t)));

for(i=2,#d, isprime(d[i-1]+d[i]) || next(2)); a=concat(a,t);break));a }

... confirms your terms (if they are to be positive) for S.

> The same seq with prime absolute differences between digits is perhaps T:

> T=1,3,5,2,4,6,8,13,14,7,9,20,24,16,18,30,25,27,29,41,31,35,36,38,50,52,42,46,

> 47,49,61,63,53,57,58,64,68,69,70,72,74,75,79,202,92,94,96,81,83,85,86,97,

> 203,130,205,207,241,302,413,131,...

Here, too, my script

EA114b(n,a=[1],u=0)={ while(#a<n, u+=1<<a[#a];

for(t=a[1]+1,9e9, bittest(u,t) & next; my(d=concat(a[#a]%10,digits(t)));

for(i=2,#d, isprime(abs(d[i-1]-d[i])) || next(2)); a=concat(a,t);break));a }

... confirms your terms if they are to be positive, and else yields:

0, 2, 4, 1, 3, 5, 7, 9, 6, 8, 13, 14, 16, 18, 30, 20, 24, 25, 27, 29,

41, 31, 35, 36, 38, 50, 52, 42, 46, 47, 49, 61, 63, 53, 57, 58, 64,

68, 69, 70, 72, 74, 75, 79, 202, 92, 94, 96, 81, 83,...

A related sequence would be that of numbers which certainly will never be in any of these sequences, like 10,13,15,17,18,19,22,24,...

which is not yet on OEIS, and between 10 and 100 close to A104211 Integers n such that the sum of the digits of n is not prime.

Best wishes,

Maximilian.

P.-S.

Dear all,

I forgot to mention that both variants of the "sum" version had already been proposed almost exactly 1 year ago, cf. A182175, A182177, A182178 and http://list.seqfan.eu/pipermail/seqfan/2012-April/009403.html where variants had been proposed by using other sets than {2,3,5,7,11,13,17} for allowed resp. forbidden digit sums.

The "abs.diff." versions are now proposed as:

A219249 (T starting with “1”),

A219250 (T starting with “0”),

... and the numbers missing in A182177, A182178 are in A219110 (while the "candidates for extending A182177, A182178 are in A182175).

Maximilian

__________

[Eric Angelini] (in a private mail to Lars):

Hello again Lars,

(sorry to invade like this -- feel free not to answer, of course)

Playing with those 2-digit sums, I was wondering if one could build a sequence W ("W" like "Waow!") where:

- all absolute differences between terms are primes

- all absolute differences between digits are primes

[...]

__________

[Lars]:

Hello again!

See 203 terms here:

W = 1, 3, 5, 2, 4, 6, 8, 13, 16, 9, 7, 20, 25, 27, 24, 29, 42, 47, 49, 46, 35, 30, 53, 50, 31, 36, 38, 57, 52, 41, 64, 61, 63, 58, 69, 72, 70, 75, 86, 81, 68, 135, 74, 79, 242, 469, 246, 83, 85, 252, 425, 202, 413, 130, 203, 136, 131, 358, 147, 94, 92, 97, 270, 241, 302, 429, 250, 207, 205, 258, 149, 418, 141, 314, 163, 14, 181, 318, 161, 352, 461, 364, 183, 142, 479, 420, 247, 96, 169, 272, 463, 146, 303, 164, 253, 186, 313, 524, 297, 274, 185, 292, 503, 505, 294, 257, 414, 275, 316, 305, 307, 296, 357, 416, 363, 502, 497, 424, 635, 702, 475, 368, 361, 350, 249, 472, 470, 279, 616, 353, 520, 369, 496, 383, 574, 641, 468, 385, 752, 525, 386, 381, 464, 613, 530, 507, 494, 631, 474, 647, 538, 527, 529, 492, 535, 746, 813, 536, 427, 968, 579, 638, 531, 614, 681, 683, 570, 572, 575, 724, 705, 703, 630, 583, 581, 618, 649, 636, 835, 792, 725, 720, 707, 946, 857, 586, 863, 696, 853, 642, 749, 646, 869, 742, 585, 758, 685, 794, 697, 920, 727, 924, 757,...

18 is the smallest number not yet used.

__________

[Eric to Lars]:

Many thanks, Lars!

[...]

Is D the right start of a seq where 2 consecutive terms sum to a prime as well as two consecutive digits?

D = 1, 2, 3, 4, 7, 6, 5, 8, 9, 20, 21, 16, 111, 112, 121, 120, 29, 212, 11, 12, 125, 234, 149,...

Best,

É.

__________

Hello Eric!

I found the first 215 terms of D to be:

D = 1, 2, 3, 4, 7, 6, 5, 8, 9, 20, 21, 16, 111, 112, 121, 120, 29, 212, 11, 12, 125, 234, 149, 230, 203, 216, 143, 258, 305, 252, 167, 432, 161, 116, 123, 214, 165, 202, 129, 238, 303, 298, 321, 250, 207, 412, 307, 612, 325, 232, 141, 256, 505, 292, 147, 416, 503, 294, 323, 434, 389, 438, 349, 474, 347, 414, 329, 492, 385, 676, 525, 656, 507, 430, 211, 498, 341, 470, 383, 476, 521, 650, 23, 830, 741, 658, 523, 838, 343, 850, 583, 856, 567, 494, 707, 614, 705, 616, 565, 652, 529, 832, 921, 1216, 561, 670, 589, 834, 749, 852, 925, 858, 929, 894, 703, 898, 585, 674, 765, 892, 985, 2034, 743, 2058, 941, 1112, 1125, 2038, 3021, 1232, 947, 4112, 989, 2030, 747, 4114, 1123, 2520, 2029, 2020, 2307, 4120, 2023, 2050, 2161, 1212, 949, 2052, 1111, 1230, 767, 4320, 761, 1116, 1121, 1250, 2021, 1238, 923, 2076, 1141, 1252, 1129, 2074, 1143, 2114, 1205, 6116, 1167, 4702, 1147, 4302, 3029, 2070, 2141, 1202, 1149, 2032, 1611, 1120, 2329, 2112, 1207, 4116, 1165, 2056, 1161, 1256, 1203, 2116, 1411, 1432, 3025, 2502, 5021, 1430, 2111, 1416, 5203, 2320, 2121, 1292, 1211, 1476, 7025, 8502, 5207, 6114, 943, 2920, 2167, 6120, 2123, 2120, 2303,...

The smallest number not used is 14 even up to terms < 10^6.

__________

[Eric to SeqFans]:

Will 14 show up one day?

[Hans Haverman]:

Assume that it does. Let the number preceding it be x. The final digit of x must be 1, 2, 4, or 6 in order for the sum of that digit and the first digit of 14 to be prime. Now, x + 14 must also be prime, but the final digit of x + 14 will be 5, 6, 8, or 0 and there is no prime ending in that. Therefore x does not exist and 14 will not show up.

__________

[Lars] (extending nicely those ideas):

If we want a sequence with maximum "primality" in it, how about L:

- All terms are prime

- Concatenation of 2 adjacent digits is prime

- Concatenation of 2 adjacent terms is prime

I found 345 terms of L using primes <= 99999989 as candidates

L = 1, 3, 7, 19, 73, 1117, 31, 37, 97, 373, 13, 1171, 11131, 11113, 79, 71713, 17137, 11173, 11719, 717979, 71719, 731173, 111373, 11197, 313, 71971, 11731, 13171, 11119, 731737, 113719, 719731, 379, 737119, 797119, 7171111, 37117, 19717, 11311, 97117, 17971, 11971, 71119, 737179, 797311, 97171, 17317, 113173, 113731, 11317, 117979, 731113, 13711, 37171, 71317, 131371, 117373, 117973, 113131, 131713, 111973, 119737, 179719, 71111137, 131113, 117319, 711973, 131731, 137119, 7137313, 131797, 173713, 179737, 311197, 137131, 713737, 131311, 311371, 113797, 119797, 173137, 313717, 197371, 197311, 311137, 131317, 311173, 737131, 317179, 7117171, 311713, 197137, 371719, 7171711, 137197, 313711, 371131, 197971, 317371, 311737, 371797, 979717, 371179, 71171797, 1137973, 719713, 1317319, 731719, 797131, 317971, 371737, 971713, 1171117, 371311, 317197, 1373173, 1313731, 1171111, 1117117, 373717, 371971, 1313797, 373171, 1731313, 1973197, 3111313, 1717117, 1373137, 1973113, 731713, 1117111, 1797379, 7379731, 971197, 971371, 1319737, 3111973, 7373719, 7131373, 1379797, 1971313, 7311313, 1111711, 1973731, 3171313, 1979713, 1711117, 3119737, 3111319, 7319713, 1737979, 7131379, 7311373, 1797319, 7971973, 1131973, 1797373, 1131379, 7313113, 1973737, 3119797, 3137311, 3131137, 3717313, 7979737, 3713737, 3173119, 71371711, 3119713, 1319719, 7973131, 3131311, 1137313, 7197313, 7137379, 71111713, 11179717, 3131173, 1731979, 7971373, 11173111, 3137179, 7373797, 3179797, 3719713, 7973137, 3711313, 11113111, 3731731, 3131113, 11171137, 3719797, 3137371, 3197137, 3731173, 11111119, 7379797, 3717319, 71111197, 3113197, 3731713, 11113171, 3797371, 3731311, 3731137, 9711379, 79731313, 11171317, 9711979, 71111113, 11111173, 11131111, 3137137, 3737311, 3797113, 11717317, 9713131, 3711319, 71117119, 71719717, 3737131, 11173711, 3717979, 71713111, 3737179, 7319737, 3731737, 9731713, 11171179, 71717119, 71311717, 3737197, 9717313, 11171371, 9737173, 11311117, 3737137, 9713713, 11713717, 9737113, 11111311, 9797311, 9797173, 13197313, 11111131, 11171731, 9713113, 11173171, 11131171, 11713111, 9797113, 11197117, 9711319, 71131717, 9731317, 3797179, 71113111, 11711311, 11711137, 11711731, 9737137, 11717137, 11197111, 9797371, 11711797, 9719737, 11719711, 11731171, 17117371, 11131717, 19711717, 9737971, 11713171, 11971711, 11311717, 9737197, 11971117, 11731711, 17371171, 13111117, 17111737, 31137373, 17311711, 13731973, 13737979, 71731111, 13131373, 13137973, 13731313, 17137117, 11971717, 11713711, 13131319, 71971111, 17111137, 19737973, 13197979, 71173111, 17971111, 17197111, 17117179, 71171731, 13111717, 17311171, 9719797, 13111711, 13737319, 73197973, 11717311, 19731979, 79717117, 17197171, 17111179, 71171137, 17137111, 13797379, 71173717, 13711717, 17971711, 17371117, 31313731, 31731379, 71711131, 19711711, 17171131, 37171171, 31131379, 71731717, 31131979, 73731319, 71111311, 31371313, 71117113, 71111371, 31313713, 73731379, 73117117, 31797379, 71711737, 97197973, 73137373, 17179717, 31117171, 31197319, 73197979,...

The list of candidates not used starts like this:

2, 5, 11, 17, 23, 29, 41, 43, 47, 53, 59, 61, 67, 71, 83, 89, 113, 131, 137, 173, 179, 197, 311, 317, 419, 431, 479, 613, 617, 619, 673, 719, 797, 971,

The smallest value not used is 2, which makes sense because including 2 means there must be a two digit number ending in 2 which is not prime. The same goes for 5.

/Lars B

__________

Beautiful seq, Lars! (Does L stand for Lars ;-)

And many thanks to all contributors!

Best,

É.