Flagpole

of themselves (sequences)

Hello SeqFans,

a little word sequence not (yet?) in the OEIS:

1 O N E

7 S E V E N

3 T H R E E

6 S I X

5 F I V E

11 E L E V E N

8 E I G H T

9 N I N E

2 T W O

13 T H I R T E E N

4 F O U R

10 T E N

12 T W E L V E

16 S I X T E E N

15 F I F T E E N

26 T W E N T Y S I X

14 F O U R T E E N

18 E I G H T E E N

17 S E V E N T E E N

19 N I N E T E E N

20 T W E N T Y

111 O N E H U N D R E D E L E V E N

21 T W E N T Y O N E

25 T W E N T Y F I V E

22 T W E N T Y T W O

23 T W E N T Y T H R E E

24 T W E N T Y F O U R

28 T W E N T Y E I G H T

38 T H I R T Y E I G H T

30 T H I R T Y

27 T W E N T Y S E V E N

29 T W E N T Y N I N E

... I

N

E

T

W

O

Explanation: the (yellow) "single letter column" (the "flagpole"), spells vertically O N E S E V E N ... which is the sequence itself. In extending the sequence, always try to use the smallest Natural not yet present in the sequence.

Is the sequence a permutation of the Naturals?

[Hans Havermann]:

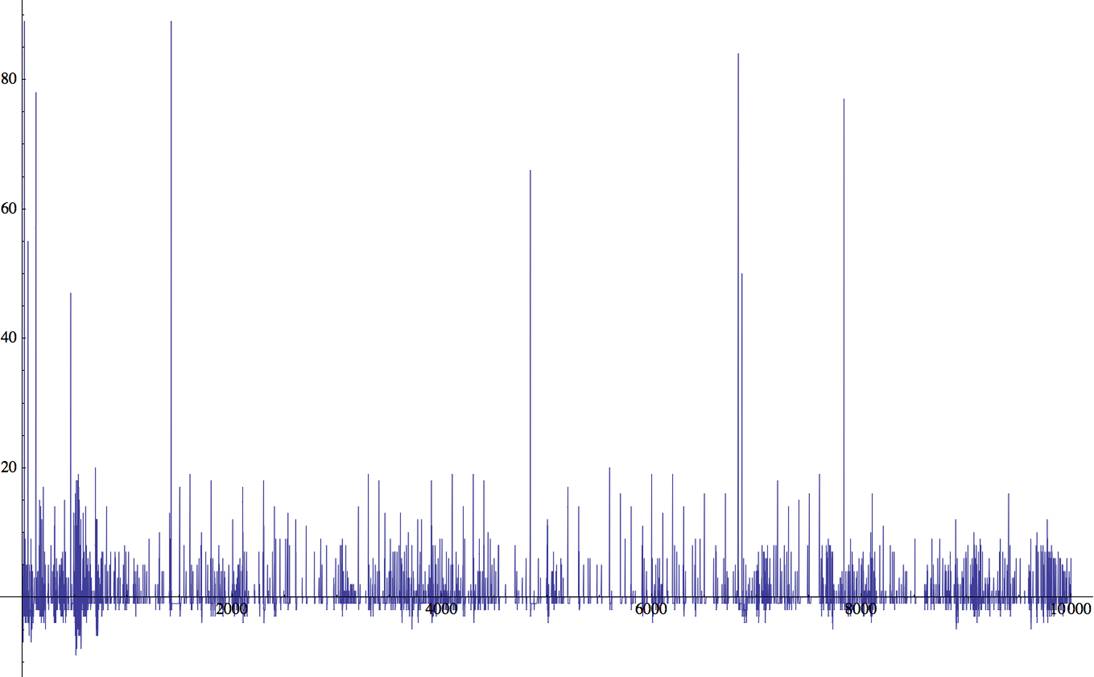
The terms of this sequence are pretty close to a straight line. In fact, of the first 10000 terms, I count 5832 where a(n) = n, beginning with n = 1, 3, 5, 15, 18, 28, 30, 45, 65, 113, ..., and the variances from this line for the rest is (in this range) relatively small:

[Eric Angelini]:

Below is the same idea as above -- but with integers instead (the yellow "digit column b" spells the digits of the sequence):

Digit column: a b c

1

2

3

4

5

6

7

8

9

1 0

2 0

1 2

3 0

1 1

2 1

1 3

4 0

1 4

1 5

2 2

1 6

1 7

2 3

2 4

5 0

1 8

3 4

1 9

2 5

2 6

2 7

.

.

.

The above sequence 1,2,3,4,5,6,7,8,9,10,20,12,30,11,21,13,40,14,15, 22,16,17,23,24,50,18,34,19,25,26,27,... is for sure a permutation of the Naturals.

And if this "flagpole" idea is worth entering the OEIS, then one could add a lot of such sequences:

Fla*Prime would start: 2,3,5,7,11,13,17,23,19,37,29,31,41,59,37,47,...

Fla*Fibo would start: 0,1,1,2,3,5,8,13,34,233,144,21,46368,121393,...

Fla*Even would start: 2,4,6,8,10,20,12,30,14,22,32,40,16,24,26,28,...

[Claudio Meller]:

Fla in Spanish: 1, 5, 2, 4, 6, 9, 8, 11, 10, 12, 3, 13, 15, 14, 7, 23, 18, 16, 17, 19, 22, 20, 24, 25, 26, ....

[Éric Angelini]:

Fla in French: 1, 5, 25, 3, 9, 4, 20, 6, 11, 21, 7, 35, 8, 15, 14, 13, 23, 12, 10, 16, 19, 2, 18, 29, 24, 22, 34, 17, 30, 27, 26, 28, 31, 80, 32, 33, 36, 42, 43, 37, 71, 38, ...

U N

C I N Q

V I N G T-C I N Q

T R O I S

N E U F

Q U A T R E

V I N G T

S I X

O N Z E

V I N G T E T U N

S E P T

T R E N T E-C I N Q

H U I T

Q U I N Z E

Q U A T O R Z E

T R E I Z E

V I N G T-T R O I S

D O U Z E

D I X

S E I Z E

D I X-N E U F

D E U X

D I X-H U I T

V I N G T-N E U F

V I N G T-Q U A T R E

V I N G T-D E U X

T R E N T E-Q U A T R E

D I X-S E P T

T R E N T E

V I N G T-S E P T

V I N G T-S I X

V I N G T-H U I T

T R E N T E E T U N

Q U A T R E-V I N G T S

T R E N T E-D E U X

T R E N T E-T R O I S

T R E N T E-S I X

Q U A R A N T E-D E U X

Q U A R A N T E-T R O I S

T R E N T E-S E P T

S O I X A N T E E T O N Z E

T R E N T E-H U I T

...

[Hans Havermann]:

I had a hunch that the linear behaviour that I charted might have been a small-numbers-only phenomenon so I decided to calculate one million terms to see if the small variances continued. I’m only just past 324000 terms (so far) when I decided to have a look:

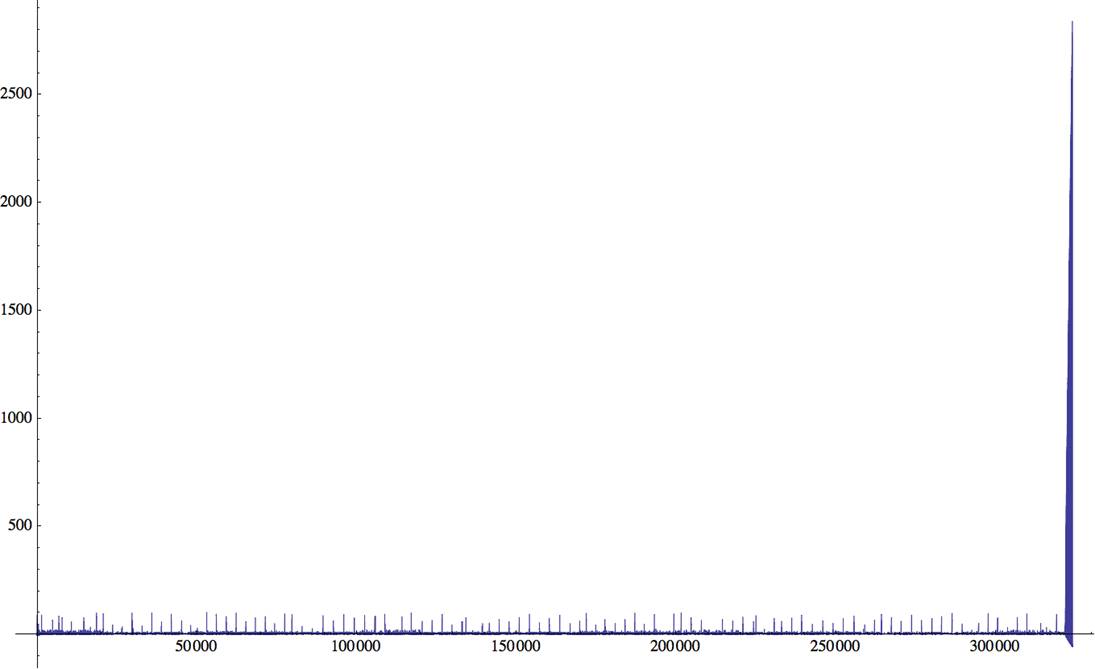
It appears that a correspondence search for the letter ‘L’ is responsible for the increasing positive variances starting with term 321680:

321680 + 31 three hundred twenty-one thousand seven hundred eleven

321859 + 52 three hundred twenty-one thousand nine hundred eleven

321873 + 39 three hundred twenty-one thousand nine hundred twelve

321890 + 121 three hundred twenty-two thousand eleven

321909 + 103 three hundred twenty-two thousand twelve

321927 + 184 three hundred twenty-two thousand one hundred eleven

321945 + 167 three hundred twenty-two thousand one hundred twelve

321962 + 249 three hundred twenty-two thousand two hundred eleven

321983 + 229 three hundred twenty-two thousand two hundred twelve

322002 + 309 three hundred twenty-two thousand three hundred eleven

322021 + 291 three hundred twenty-two thousand three hundred twelve

322039 + 372 three hundred twenty-two thousand four hundred eleven

322056 + 356 three hundred twenty-two thousand four hundred twelve

322078 + 433 three hundred twenty-two thousand five hundred eleven

322092 + 420 three hundred twenty-two thousand five hundred twelve

322098 + 513 three hundred twenty-two thousand six hundred eleven

322114 + 498 three hundred twenty-two thousand six hundred twelve

322118 + 593 three hundred twenty-two thousand seven hundred eleven

322140 + 572 three hundred twenty-two thousand seven hundred twelve

322161 + 650 three hundred twenty-two thousand eight hundred eleven

322183 + 629 three hundred twenty-two thousand eight hundred twelve

322208 + 703 three hundred twenty-two thousand nine hundred eleven

322231 + 681 three hundred twenty-two thousand nine hundred twelve

322251 + 760 three hundred twenty-three thousand eleven

322275 + 737 three hundred twenty-three thousand twelve

322297 + 814 three hundred twenty-three thousand one hundred eleven

322320 + 792 three hundred twenty-three thousand one hundred twelve

322343 + 868 three hundred twenty-three thousand two hundred eleven

322367 + 845 three hundred twenty-three thousand two hundred twelve

322390 + 921 three hundred twenty-three thousand three hundred eleven

322413 + 899 three hundred twenty-three thousand three hundred twelve

322438 + 973 three hundred twenty-three thousand four hundred eleven

322463 + 949 three hundred twenty-three thousand four hundred twelve

322487 + 1024 three hundred twenty-three thousand five hundred eleven

322507 + 1005 three hundred twenty-three thousand five hundred twelve

322530 + 1081 three hundred twenty-three thousand six hundred eleven

322553 + 1059 three hundred twenty-three thousand six hundred twelve

322578 + 1133 three hundred twenty-three thousand seven hundred eleven

322602 + 1110 three hundred twenty-three thousand seven hundred twelve

322624 + 1187 three hundred twenty-three thousand eight hundred eleven

322648 + 1164 three hundred twenty-three thousand eight hundred twelve

322673 + 1238 three hundred twenty-three thousand nine hundred eleven

322698 + 1214 three hundred twenty-three thousand nine hundred twelve

322722 + 1289 three hundred twenty-four thousand eleven

322741 + 1271 three hundred twenty-four thousand twelve

322764 + 1347 three hundred twenty-four thousand one hundred eleven

322788 + 1324 three hundred twenty-four thousand one hundred twelve

322810 + 1401 three hundred twenty-four thousand two hundred eleven

322834 + 1378 three hundred twenty-four thousand two hundred twelve

322857 + 1454 three hundred twenty-four thousand three hundred eleven

322879 + 1433 three hundred twenty-four thousand three hundred twelve

322901 + 1510 three hundred twenty-four thousand four hundred eleven

322925 + 1487 three hundred twenty-four thousand four hundred twelve

322948 + 1563 three hundred twenty-four thousand five hundred eleven

322967 + 1545 three hundred twenty-four thousand five hundred twelve

322989 + 1622 three hundred twenty-four thousand six hundred eleven

323013 + 1599 three hundred twenty-four thousand six hundred twelve

323035 + 1676 three hundred twenty-four thousand seven hundred eleven

323058 + 1654 three hundred twenty-four thousand seven hundred twelve

323081 + 1730 three hundred twenty-four thousand eight hundred eleven

323103 + 1709 three hundred twenty-four thousand eight hundred twelve

323127 + 1784 three hundred twenty-four thousand nine hundred eleven

323151 + 1761 three hundred twenty-four thousand nine hundred twelve

323174 + 1837 three hundred twenty-five thousand eleven

323193 + 1819 three hundred twenty-five thousand twelve

323215 + 1896 three hundred twenty-five thousand one hundred eleven

323239 + 1873 three hundred twenty-five thousand one hundred twelve

323262 + 1949 three hundred twenty-five thousand two hundred eleven

323285 + 1927 three hundred twenty-five thousand two hundred twelve

323307 + 2004 three hundred twenty-five thousand three hundred eleven

323331 + 1981 three hundred twenty-five thousand three hundred twelve

323355 + 2056 three hundred twenty-five thousand four hundred eleven

323378 + 2034 three hundred twenty-five thousand four hundred twelve

323399 + 2112 three hundred twenty-five thousand five hundred eleven

323423 + 2089 three hundred twenty-five thousand five hundred twelve

323447 + 2164 three hundred twenty-five thousand six hundred eleven

323473 + 2139 three hundred twenty-five thousand six hundred twelve

323498 + 2213 three hundred twenty-five thousand seven hundred eleven

323523 + 2189 three hundred twenty-five thousand seven hundred twelve

323547 + 2264 three hundred twenty-five thousand eight hundred eleven

323573 + 2239 three hundred twenty-five thousand eight hundred twelve

323599 + 2312 three hundred twenty-five thousand nine hundred eleven

323624 + 2288 three hundred twenty-five thousand nine hundred twelve

323649 + 2362 three hundred twenty-six thousand eleven

323669 + 2343 three hundred twenty-six thousand twelve

323692 + 2419 three hundred twenty-six thousand one hundred eleven

323715 + 2397 three hundred twenty-six thousand one hundred twelve

323738 + 2473 three hundred twenty-six thousand two hundred eleven

323762 + 2450 three hundred twenty-six thousand two hundred twelve

323786 + 2525 three hundred twenty-six thousand three hundred eleven

323811 + 2501 three hundred twenty-six thousand three hundred twelve

323836 + 2575 three hundred twenty-six thousand four hundred eleven

323861 + 2551 three hundred twenty-six thousand four hundred twelve

323885 + 2626 three hundred twenty-six thousand five hundred eleven

323905 + 2607 three hundred twenty-six thousand five hundred twelve

323928 + 2683 three hundred twenty-six thousand six hundred eleven

323951 + 2661 three hundred twenty-six thousand six hundred twelve

323975 + 2736 three hundred twenty-six thousand seven hundred eleven

323999 + 2713 three hundred twenty-six thousand seven hundred twelve

[I’ve placed a text file of terms 321500 - 324000 (so that you can better appreciate this emergent behaviour) here. It will be interesting to see how this evolves.]

...

I’ve taken this file down, because I will replace it with something much better. I’m going to do an actual flagpole down to this region, and beyond. In order to keep file-sizes relatively small, I’m breaking the pole up into 50000-term pieces, but even with that the first file is 7 MB:

http://chesswanks.com/num/flagpole/000050.txt

Depending on your browser, you might need to shrink the font-size to keep things from wrapping. There’s lots of white space (which adds to the file-size) but I’m thinking of extending the flagpole (eventually) into the millions and I expect a lot of that white space to disappear in those larger regions. So why keep the white space in the smaller regions? I want smooth annealing: If you copy/paste (part of) one file into another, I still want everything to line up.

You can see which files are available by refreshing:

http://chesswanks.com/num/flagpole

The program that is actually calculating the terms has really slowed down in this (I’m currently at 340000) region where we encounter the L-spur (spur = railroad terminology). That’s because my program starts looking at the smallest available number and increments by ones from there. For every L that it now encounters, it has to go many thousands of numbers into the search, which is not very efficient. The good news is that I fully expect things to get back on track (more railroad terminology) once the pole’s "eleven-" and "twelve-" thousands are used up and we approach the 411- and 412-thousand Ls for search finds. In other words, I’m guessing that the increasingly large a(n) = n variances generated by the letter L will stabilize at 400000, or so, and disappear soon thereafter.

[Hans Havermann] (August 24^th update):

OK. I misjudged how fast the program would run beyond 386700. I’m up to 600000.

http://chesswanks.com/num/flagpole

The next zero variance [a(n) = n] after the one at 321947 is 411273. I’ve been thinking about the supply side of specific letters. I had suggested that W might create a spur approaching 700000, because of demand, but I no longer think that. The letters E, F, G, H, I, N, O, R, S, T, U, V, W, and X occur every ten number-words, so there is always plentiful local supply for these, regardless of demand. Y less so, but still plentiful enough. L less than Y but cannot ever be a problem after we reach the -illion numbers. D is easily satisfied once we reach -hundred-, and A, once we reach -thousand- numbers. (Think of how we will supply demand for A after we reach 10^6.) That leaves M after we reach 10^9 (subsequently, B, Q, P, and C, but that is far beyond our scope). Every demand for M after 10^9 will have to travel to 10^9 + 10^6 for its supply, so this should create the next *significant* spur. I don’t think it will look like the L-spur because it will lack the gradual approach to the plateau.

I’m attaching a graph of the flagpole sequence, to 500000, superimposed on a red a(n) = n line. Most of the red line is not visible, because the flagpole sequence is so close to it. I’m also attaching a blow-up of the L-spur region.

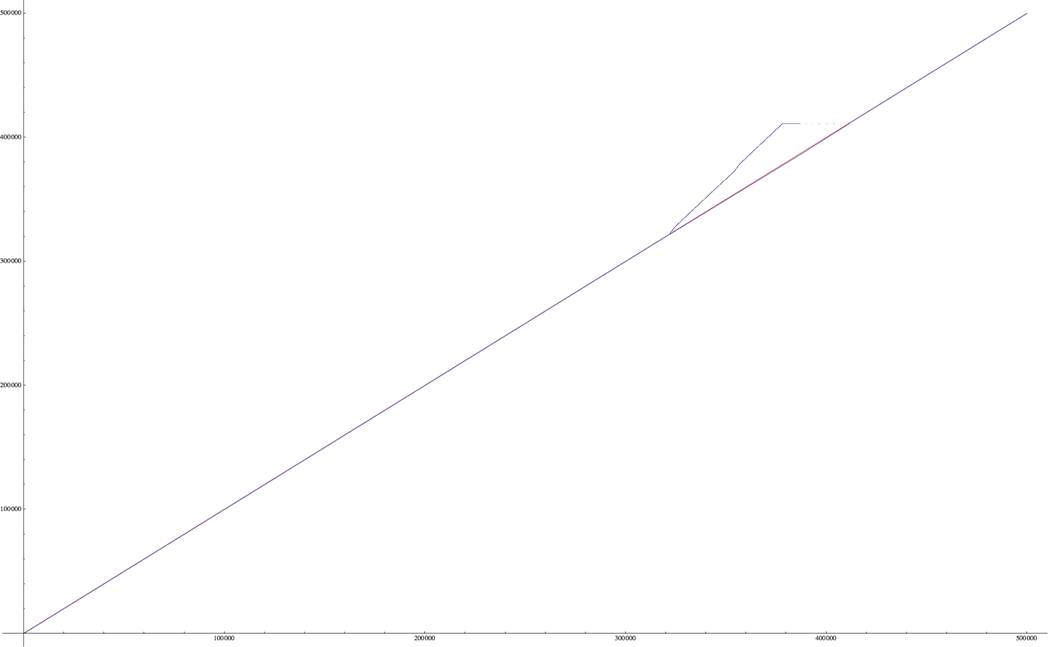
Blow up:

__________

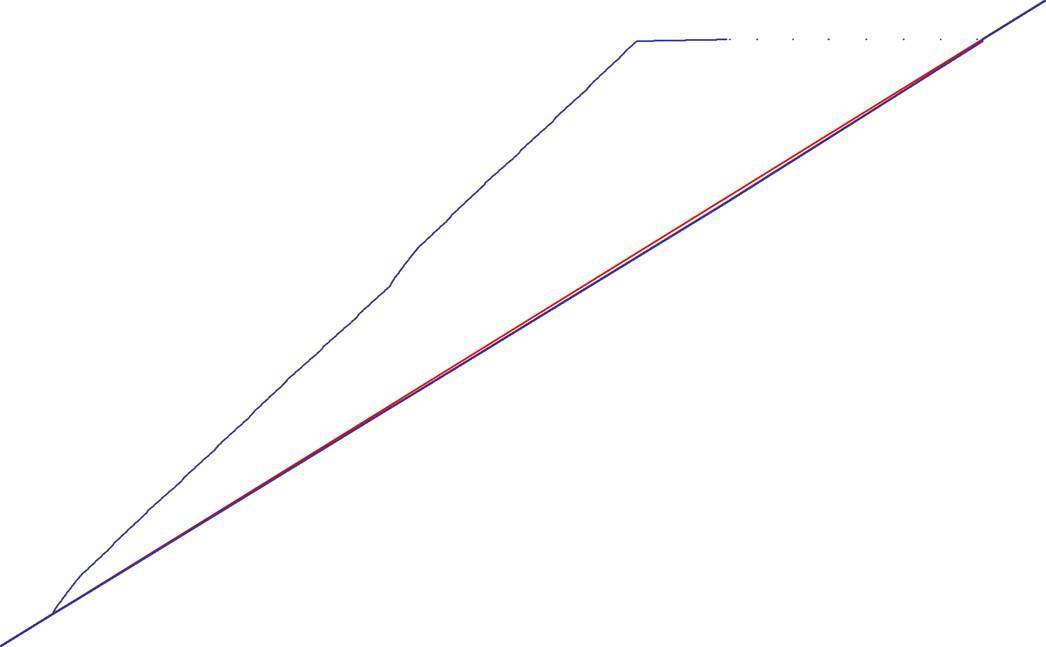
Many thanks to you, Hans and Claudio!

Best,

É.

(August 14^th 2012, Brussels, Belgium)