Vers de verres
(Glass worms)
Soit
un alignement fini de verres, contenant chacun un nombre entier d’unités de
liquide (parfois zéro –> verre vide)
Procédure :
- on
prend le verre le plus à gauche,
- on
regarde le nombre k d’unités qu’il
contient,
- on
le vide dans le k-ième
verre à sa droite,
- on
pose le verre vide tout à droite, en dernière position ;
- on
recommence la procédure.
Exemple :
\ 1 / \ 2 / \ 4 / \ 1 / \ 0
/
\_/
\_/ \_/ \_/
\_/
\ 0 / \ 3 / \ 4 / \ 1 / \ 0 /
\_/
\_/ \_/ \_/
\_/
\ 3 / \ 4 / \ 1 / \ 0 / \ 0 /
c) \_/
\_/ \_/ \_/
\_/
\ 0 / \ 4 / \ 1 / \ 3 / \ 0 /
d) \_/
\_/ \_/ \_/
\_/
\ 4 / \ 1 / \ 3 / \ 0 / \ 0 /
e) \_/
\_/ \_/ \_/
\_/
\ 0 / \ 1 / \ 3 / \ 0 / \ 4 /
f) \_/
\_/ \_/ \_/
\_/
\ 1 / \ 3 / \ 0 / \ 4 / \ 0 /
g) \_/ \_/
\_/ \_/ \_/
\ 0 / \ 4 / \ 0 / \ 4 / \ 0 /
h) \_/ \_/
\_/ \_/ \_/
\ 4 / \ 0 / \ 4 / \ 0 / \ 0 /
i) \_/ \_/
\_/ \_/ \_/
\ 0 / \ 0 / \ 4 / \ 0 / \ 4 /
j) \_/ \_/
\_/ \_/ \_/
\ 0 / \ 4 / \ 0 / \ 4 / \ 0 /
k) \_/ \_/
\_/ \_/ \_/
--> cette configuration est la même que (h)
Remarque (merci à Mitch Harris
et Jacques Tramu)
Il est
interdit de verser le contenu d’un verre ailleurs que dans un verre ! La
configuration suivante « bloque » immédiatement :
\ 4 / \ 2 / \ 0 / \ 1 /
\_/
\_/ \_/ \_/
... en effet le contenu 4 du premier verre n’a pas de
réceptacle valide. Jacques dit ça
autrement : « S'il y a N verres, la
capacité maximale de chacun est de N-1, avec interdiction de
déborder ».
Questions :
Si
l’on représente une configuration de verres sous forme de chaîne de caractères,
la séquence ci-dessus s’écrit :
(a) 12410 --> (b) 03410 --> (c) 34100 --> (d) 04130
--> (e) 41300 --> (f) 01304 --> (g) 13040 --> (h) 04040 --> (i)
40400 --> (j) 00404 --> (k) 04040 --> (h) (boucle)
Traduisons
maintenant une configuration de verres en nombre entier (quand c’est possible –
en effet une configuration commençant par un verre vide sera
« traduite » par un entier commençant pas zéro, ce qui est interdit).
Quelle serait alors la suite W(1)
des nombres entiers (tels que 12410 ou 13040) qui permettent d’entrer dans une
boucle ?
Quelle
serait la suite W(2) des plus petits
nombres entiers (tels que 40400) faisant partie d’une boucle ? [On peut
voir ces derniers comme des vers (de verres) se déplaçant vers la droite par
mues successives – d’où le titre de cette page].
__________
Jacques
Tramu a proposé (le 9 mars
2009, sur la liste SeqFans)
une troisième suite W(3),
celle des « worst worms » (les pires vers) :
What is the starting configuration which
leads to the larger number of moves, before detecting a cycle?
I’ve found the following (not exhaustive
search) sequence for glasses = 1 to 11:
number of glasses {starting configuration}
maximum moves to cycle detection
1
{ 0 } 1
2
{ 0,
1 } 2
3
{ 1, 0, 1 }
4
4
{ 0, 1, 1, 1 }
7
5
{ 0, 1, 0, 2, 1 }
10
6
{ 3, 0, 0, 0, 0, 2 } 13
7
{ 2, 0, 0, 5, 4, 4, 1 }
20
8
{ 0, 0, 0, 2, 2, 2, 0, 1 }
22
9
{ 1, 5, 1, 1, 1, 2, 0, 0, 3 }
42
10
{ 3, 0, 4, 2, 1, 0, 0, 1, 0, 3 }
43
11
{ 0, 3, 0, 1, 4, 0, 5, 10, 1, 1, 3 } 63
Example:
{ 1, 0, 1 }
{ 1, 1, 0 } move 1
{ 2, 0, 0 } move 2
{ 0, 2, 0 } move 3
{ 2, 0, 0 } move 4 <-- cycle detection
On voit à la ligne 9 du tableau de Jacques que le vers (et le nombre) 151112003 met 42 générations à
se régénérer !
Les dix premiers termes de W(3)
pourraient donc être (colonne de droite du tableau ci-dessus) :
W(3) = 1, 2, 4, 7,
10, 13, 20, 22, 42, 43, 63, ...
À la ligne 11 du tableau apparaît un contenu (en gris) qui est
supérieur à 9 ; le vers {0,3,0,1,4,0,5,10,1,1,3} n’est donc pas
immédiatement traduisible en nombre entier (il commence d’ailleurs par zéro, ce
qui est interdit).
Jacques a pensé à une
quatrième suite W(4), celle du
nombre de configurations légales de
départ correspondant à un nombre de verres donné. Une configuration
légale ? On a vu qu’un verre ne peut avoir qu’un contenu inférieur ou égal
au nombre de verres en jeu. La configuration suivante est donc illégale :
\ 4 / \ 2 / \ 0 / \ 1 /
\_/
\_/ \_/ \_/
Qui calculera W(4) ?
Jacques, bien sûr ! Voici un début de tableau :
Nbre de verres / Config.
de dép. légales / Config.
possibles
0 1 1
1 1
1
2 3 4
3 13 27
4 64 256
5 404 3125
6 2135 46656
7 21077 823543
8 111459 16777216
...
W(4) = 1, 1, 3,
13, 64, 404, 2135, 21077, 111459, ...
La colonne des configurations possibles est la suite A000312 dans
l’OEIS de Neil Sloane.
__________
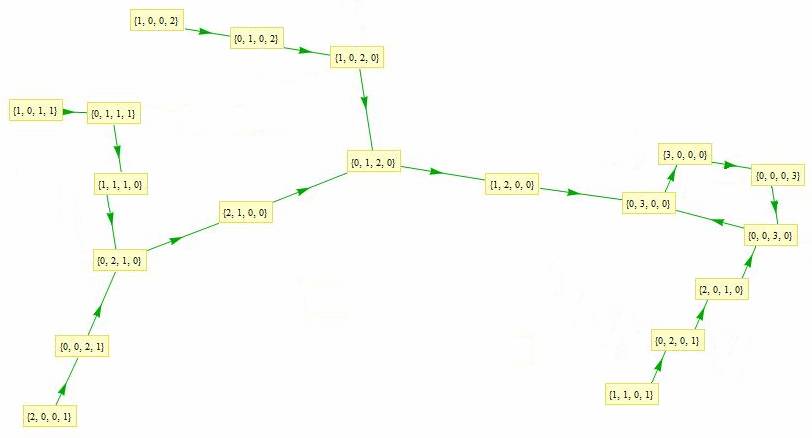
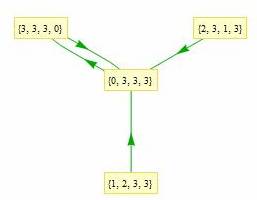
Jean-Marc Falcoz a dessiné le 10 mars 2009 tous les parcours des
vers légaux de longueur 4 ; boucles et attracteurs sont bien
visibles :
![]()
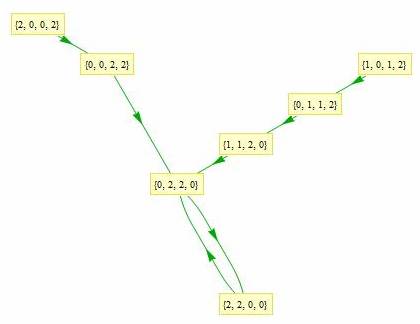

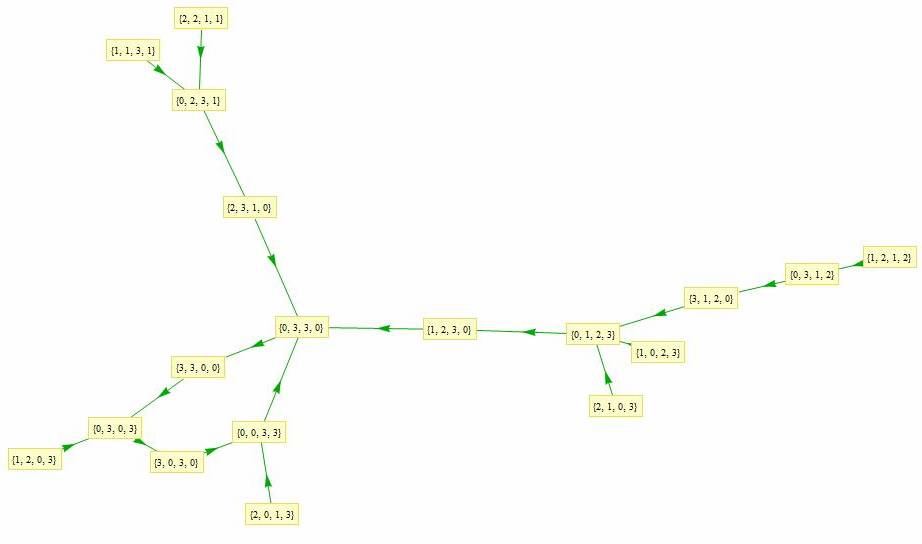
Tous les vers légaux de longueur 2 à 6 sont là
(merci à Jean-Marc)
__________
Retour à la page
d’accueil, là.