King Walking
[July, 23rd,
2010]
Hello SeqFans,
In this 4x5 box
one can read all consecutive integers from 0 to 158 (included):
5 8 0 7
3
9 6 5 1
8
1 3 2 4
2
4 0 9 7
6
(grid submitted by James
Dow Allen on rec.puzzles
two days ago)
The rules are:
- an integer is there if its digits can be walked on by a
chess King (one step in 8 directions: 4 straightly, 4 diagonally)
- two identical digits (or more) can follow each other (as if
the King was jumping on the same square).
Example:
- the integers 58073, 13997 and 13887 are visible below,
- the integer 159 is not:
5 8 0 7 3
9 6 5 1 8
1 3 2 4 2
4 0 9 7 6
It seems
impossible to find such a 4x5 box showing all consecutive integers from 0 to n
with n > 158.
Here is Giovanni Restas 158 solution
or the same box published on rec.puzzles yesterday):
0 3 6 4
2
1 7 5 1
3
4 0 2 8
9
8 9 6 5
7
Question:
Using the same
rules, what would be the highest reachable integer in the successive square
boxes 1x1, 2x2, 3x3, 4x4, 5x5, ...
This might
constitute a seq S for Neil. [S starts 0, 3, 8, ...]
Best,
Ι.
__________
[Andrew Weimholt]:
> The next term is
at least 58
8 3 4 9
2 0 7 2
1 6 5 1
9 3 4 8
I looked a little closer at this
one tonight, and I can now also confirm
that 58 is the next term.
__________
[Dmitri Kamenetsky]:
Hi Eric,
What an interesting problem,
thank you! This problem seems perfect
for our competitions: http://www.v-sonline.com/index.pl
I will propose
the problem and if it gets accepted then
we will probably
explore all NxN squares with
N from 3 to 32.
__________
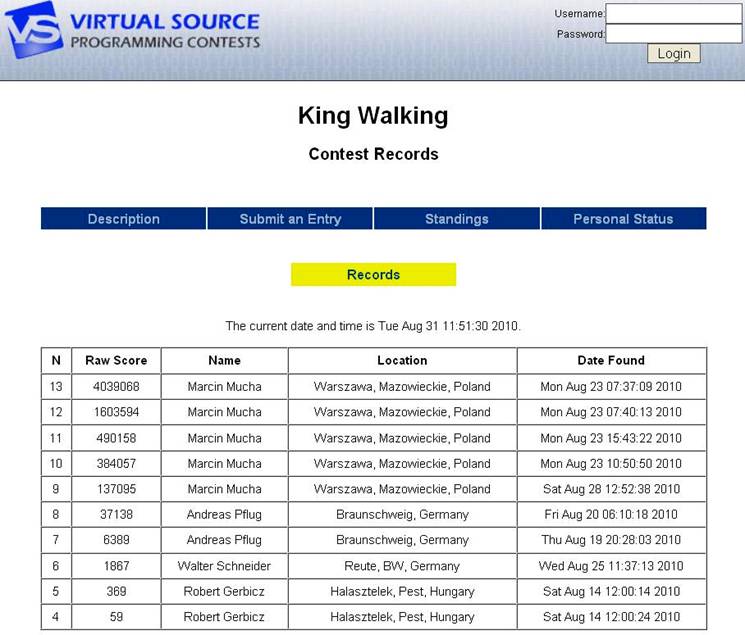
... and so it was the contest asking though for N to be kept between
4 and 13. The sequence (including the substring 0, which was not specified on
SeqFans) is currently this one
(September 1st, 2010):
S = 1, 4, 9, 59,
369, 1867, 6389, 37138, 137095, 384057, 490158, 1603594, 4039068, ...
To be followed ?
Best,
Ι.
__________