n’ = (MAXd+MINd)/2

Hello SeqFans,

Let’s start with n = 723810.

We read n from left to right, digit by digit, in this way:

7 says: replace me by the biggest of the 7 digits on my right (including me)

Then 7 is replaced by 8 --> n = 823810

2 says: replace me by the biggest of the 2 digits on my right (including me)

Then 2 is replaced by 3 --> n = 833810

3 says: replace me by the biggest of the 3 digits on my right (including me)

Then 3 is replaced by 8 --> n = 838810

8 says: replace me by the biggest of the 8 digits on my right (including me)

Then 8 is replaced by 8 --> n = 838810

1 says: replace me by the biggest of the 1 digit(s) on my right (including me)

Then 1 is replaced by 1 --> n = 838810

0 says: replace me by the biggest of the 0 digit(s) on my right (including me)

Then 0 is replaced by nothing and disappears --> n = 83881

So n = 723810 becomes 83881. This result is called MAXd (maximum digit)

The MINd (minimum digit) operation works in the same way (just replace "biggest" by "smallest", above).

We then get for n: 723810 --> 02101 which is 2101.

We will now transform n into n’:

n’ = (MAXd+MINd)/2

For n = 723810 we have n’ = (83881+2101)/2 = 42991

We could then iterate from there. But we will see first what happens with n = 1234 and present the iteration like this:

/ MAXd / MAXd’

n MAXd+MINd = n’ MAXd’+MINd’ = n", etc.

\ MINd \ MINd’

/1344 /1899 /1994 /1919 /1919

1234 2578 = 1289 3188 = 1594 3438 = 1719 3038 = 1519 3038 = 1519

\1234 \1289 \1444 \1119 \1119

... we see that 1519 is a fixed point.

What would be S, the "fixed-points" sequence of (MAXd+MINd)/2?

S starts, I think, like this:

S = 1,2,3,4,5,6,7,8,9,11,12,13,14,15,16,17,18,19,22, ...

Could we have (MAXd+MINd) = odd number? Yes, in a (very) few cases:

30 3 = 1,5

If so, the iteration stops as "impossible".

Best,

É.

__________

Douglas McNeil:

> S = 1,2,3,4,5,6,7,8,9,11,12,13,14,15,16,17,18,19,22, ...

Agreed: I find

sage: S

[1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18, 19, 22, 33, 44, 55, 66, 77, 88, 99, 111, 112, 113, 114, 115, 116, 117, 118, 119, 122, 133, 144, 155, 166, 177, 188, 199, 222, 315, 333, 417, 444, 519, 555, 666, 777, 888, 999, 1111, 1112, 1113, 1114, 1115, 1116, 1117, 1118, 1119, 1122, 1133, 1144, 1155, 1166, 1177, 1188, 1199, 1222, 1315, 1333, 1417, 1444, 1519, 1555, 1666, 1777, 1888, 1999, 2222, 3155, 3333, 3519, 4117, 4177, 4417, 4444, 5119, 5199, 5519, 5555, 6666, 7777, 8888, 9999]

> Could we have (MAXd+MINd) = odd number? Yes, in a (very) few cases:

Not so rare-- I think any multiple of 10 with a last nonzero digit being 3,5,7, or 9 will produce an odd number.

sage: O[:100]

[30, 50, 70, 90, 130, 150, 170, 190, 230, 250, 270, 290, 300, 330, 350, 370, 390, 430, 450, 470, 490, 500, 530, 550, 570, 590, 630, 650, 670, 690, 700, 730, 750, 770, 790, 830, 850, 870, 890, 900, 930, 950, 970, 990, 1030, 1050, 1070, 1090, 1130, 1150, 1170, 1190, 1230, 1250, 1270, 1290, 1300, 1330, 1350, 1370, 1390, 1430, 1450, 1470, 1490, 1500, 1530, 1550, 1570, 1590, 1630, 1650, 1670, 1690, 1700, 1730, 1750, 1770, 1790, 1830, 1850, 1870, 1890, 1900, 1930, 1950, 1970, 1990, 2030, 2050, 2070, 2090, 2130, 2150, 2170, 2190, 2230, 2250, 2270, 2290]

__________

Maximilian Hasler:

Je trouve pour les points fixes :

S =

1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18, 19, 22, 33, 44, 55, 66, 77, 88, 99, 111, 112, 113, 114, 115, 116, 117, 118, 119, 122, 133, 144, 155, 166, 177, 188, 199, 222, 315, 333, 417, 444, 519, 555, 666, 777, 888, 999, 1111, 1112, 1113, 1114, 1115, 1116, 1117, 1118, 1119, 1122, 1133, 1144, 1155, 1166, 1177, 1188, 1199, 1222, 1315, 1333, 1417, 1444, 1519, 1555, 1666, 1777, 1888, 1999, 2222, 3155, 3333, 3519, 4117, 4177, 4417, 4444, 5119, 5199, 5519, 5555, 6666, 7777, 8888, 9999, 11111, 11112, 11113, 11114, 11115, 11116, 11117, 11118, 11119, 11122, 11133, 11144, 11155, 11166, 11177, 11188, 11199, 11222, 1315, 11333, 11417, 11444, 11519, 11555, 11666, 11777, 11888, 11999, 12222, 13155, 13333, 13519, 14117, 14177, 14417, 14444, 15119, 15199, 15519, 15555, 16666, 17777, 18888, 19999, 22222, 31519, 31555, 33333, 35119, 35199, 41177, 41777, 44177, 44444, 51119, 51199, 51519, 51999, 53519, 55119, 55199, 55519, 55555, 66666, 77777, 88888, 99999, ...

... et pour les archives, le code :

MAXd(n)={ for(i=1,#n=Vecsmall(Str(n)), if( n[i]>48, for(j=i+1,min(#n,i+n[i]-49),

n[j]>n[i] & n[i]=n[j]), n[i]=32)); eval(Strchr(n)) }

MINd(n)={ for(i=1,#n=Vecsmall(Str(n)), if( n[i]>48, for(j=i+1,min(#n,i+n[i]-49),

n[j]<n[i] & n[i]=n[j]), n[i]=32)); eval(Strchr(n)) }

EA(n)=(MAXd(n)+MINd(n))/2

for(n=1,99999,EA(n)==n & print1(n", "))

__________

Jean-Marc Falcoz:

(...)

J’ai regardé ce que donnait la suite en allant jusqu’à 20 000 000 :

{1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18, 19, 22, 33, 44, 55, 66, 77, 88, 99, 111, 112, 113, 114, 115, 116, 117, 118, 119, 122, 133, 144, 155, 166, 177, 188, 199, 222, 315, 333, 417, 444, 519, 555, 666, 777, 888, 999, 1111, 1112, 1113, 1114, 1115, 1116, 1117, 1118, 1119, 1122, 1133, 1144, 1155, 1166, 1177, 1188, 1199, 1222, 1315, 1333, 1417, 1444, 1519, 1555, 1666, 1777, 1888, 1999, 2222, 3155, 3333, 3519, 4117, 4177, 4417, 4444, 5119, 5199, 5519, 5555, 6666, 7777, 8888, 9999, 11111, 11112, 11113, 11114, 11115, 11116, 11117, 11118, 11119, 11122, 11133, 11144, 11155, 11166, 11177, 11188, 11199, 11222, 11315, 11333, 11417, 11444, 11519, 11555, 11666, 11777, 11888, 11999, 12222, 13155, 13333, 13519, 14117, 14177, 14417, 14444, 15119, 15199, 15519, 15555, 16666, 17777, 18888, 19999, 22222, 31519, 31555, 33333, 35119, 35199, 41177, 41777, 44177, 44444, 51119, 51199, 51519, 51999, 53519, 55119, 55199, 55519, 55555, 66666, 77777, 88888, 99999, 111111, 111112, 111113, 111114, 111115, 111116, 111117, 111118, 111119, 111122, 111133, 111144, 111155, 111166, 111177, 111188, 111199, 111222, 111315, 111333, 111417, 111444, 111519, 111555, 111666, 111777, 111888, 111999, 112222, 113155, 113333, 113519, 114117, 114177, 114417, 114444, 115119, 115199, 115519, 115555, 116666, 117777, 118888, 119999, 122222, 131519, 131555, 133333, 135119, 135199, 141177, 141777, 144177, 144444, 151119, 151199, 151519, 151999, 153519, 155119, 155199, 155519, 155555, 166666, 177777, 188888, 199999, 222222, 315119, 315199, 315519, 315555, 333333, 351119, 351199, 351519, 351999, 411777, 417777, 441777, 444444, 453519, 511199, 511999, 515199, 519999, 535199, 551199, 551999, 555199, 555555, 666666, 777777, 888888, 999999, 1111111, 1111112, 1111113, 1111114, 1111115, 1111116, 1111117, 1111118, 1111119, 1111122, 1111133, 1111144, 1111155, 1111166, 1111177, 1111188, 1111199, 1111222, 1111315, 1111333, 1111417, 1111444, 1111519, 1111555, 1111666, 1111777, 1111888, 1111999, 1112222, 1113155, 1113333, 1113519, 1114117, 1114177, 1114417, 1114444, 1115119, 1115199, 1115519, 1115555, 1116666, 1117777, 1118888, 1119999, 1122222, 1131519, 1131555, 1133333, 1135119, 1135199, 1141177, 1141777, 1144177, 1144444, 1151119, 1151199, 1151519, 1151999, 1153519, 1155119, 1155199, 1155519, 1155555, 1166666, 1177777, 1188888, 1199999, 1222222, 1315119, 1315199, 1315519, 1315555, 1333333, 1351119, 1351199, 1351519, 1351999, 1411777, 1417777, 1441777, 1444444, 1453519, 1511199, 1511999, 1515199, 1519999, 1535199, 1551199, 1551999, 1555199, 1555555, 1666666, 1777777, 1888888, 1999999, 2222222, 3151119, 3151199, 3151519, 3151999, 3153519, 3155119, 3155199, 3155519, 3155555, 3333333, 3511199, 3511999, 3515199, 3519999, 4117777, 4177777, 4417777, 4444444, 4453519, 4535199, 5111999, 5119999, 5151999, 5199999, 5351999, 5511999, 5519999, 5551999, 5555555, 6666666, 7777777, 8888888, 9999999, 11111111, 11111112, 11111113, 11111114, 11111115, 11111116, 11111117, 11111118, 11111119, 11111122, 11111133, 11111144, 11111155, 11111166, 11111177, 11111188, 11111199, 11111222, 11111315, 11111333, 11111417, 11111444, 11111519, 11111555, 11111666, 11111777, 11111888, 11111999, 11112222, 11113155, 11113333, 11113519, 11114117, 11114177, 11114417, 11114444, 11115119, 11115199, 11115519, 11115555, 11116666, 11117777, 11118888, 11119999, 11122222, 11131519, 11131555, 11133333, 11135119, 11135199, 11141177, 11141777, 11144177, 11144444, 11151119, 11151199, 11151519, 11151999, 11153519, 11155119, 11155199, 11155519, 11155555, 11166666, 11177777, 11188888, 11199999, 11222222, 11315119, 11315199, 11315519, 11315555, 11333333, 11351119, 11351199, 11351519, 11351999, 11411777, 11417777, 11441777, 11444444, 11453519, 11511199, 11511999, 11515199, 11519999, 11535199, 11551199, 11551999, 11555199, 11555555, 11666666, 11777777, 11888888, 11999999, 12222222, 13151119, 13151199, 13151519, 13151999, 13153519, 13155119, 13155199, 13155519, 13155555, 13333333, 13511199, 13511999, 13515199, 13519999, 14117777, 14177777, 14417777, 14444444, 14453519, 14535199, 15111999, 15119999, 15151999, 15199999, 15351999, 15511999, 15519999, 15551999, 15555555, 16666666, 17777777, 18888888, 19999999}

Si l’on ne s’occupe que de la liste de tous les chiffres obtenus, on voit qu’on a une suite quasi fractale, certains nombres ont une trajectoire évidente avant de se stabiliser :

144

1444

etc.

Pour d’autres c’est un peu moins évident :

519

3519

53519

453519

4453519

14453519

114453519

1114453519

11114453519

etc.

Vraiment étrange !

Entre 10^j et 10^(j+1) , on garde les mêmes nombres en rajoutant un 1 devant, mais on a aussi de nouvelles branches qui se créent, par ex. 151999 donne naissance à 1151999, mais aussi à 5151999

ou encore, quand on examine dans la suite les nombres ne contenant que des 1, des 4 et des 7 (par exemple) :

417

1417

4117

4177

4417

11417

14117

14177

14417

41177

41777

44177

111417

114117

114177

114417

141177

141777

144177

411777

417777

441777

1111417

1114117

1114177

1114417

1141177

1141777

1144177

1411777

1417777

1441777

4117777

4177777

4417777

11111417

11114117

11114177

11114417

11141177

11141777

11144177

11411777

11417777

11441777

14117777

14177777

14417777

...

on voit que les branches se développent régulièrement, mais créent aussi des rejetons !

Pour visualiser le côté "fractal perturbé" de cette suite, j’ai dessiné la trajectoire correspondant aux chiffres composant la suite des nombres, c’est à dire :

1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 1, 1, 2, 1, 3, 1, 4, 1, 5, 1, 6, 1, 7, 1, 8, 1, 9, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9, 1, 1, 1, 1, 1, 2, 1, 1, 3, 1, 1, 4, 1, 1, 5, 1, 1, 6, 1, 1, 7, 1, 1, 8, 1, 1, 9, 1, 2, 2, 1, 3, 3, 1, 4, 4, 1, 5, 5, 1, 6, 6, 1, 7, 7, 1, 8, 8, 1, 9, 9, 2, 2, 2, 3, 1, 5, 3, 3, 3, 4, 1, 7, 4, 4, 4, 5, 1, 9, 5, 5, 5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 9, 9, 9, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 3, 1, 1, 1, 4, 1, 1, 1, 5, 1, 1, 1, 6...

en assignant une direction à chaque chiffre (1=40°, 2=80°, etc.) On voit que cette suite forme un motif qui se répète en se déformant peu à peu :

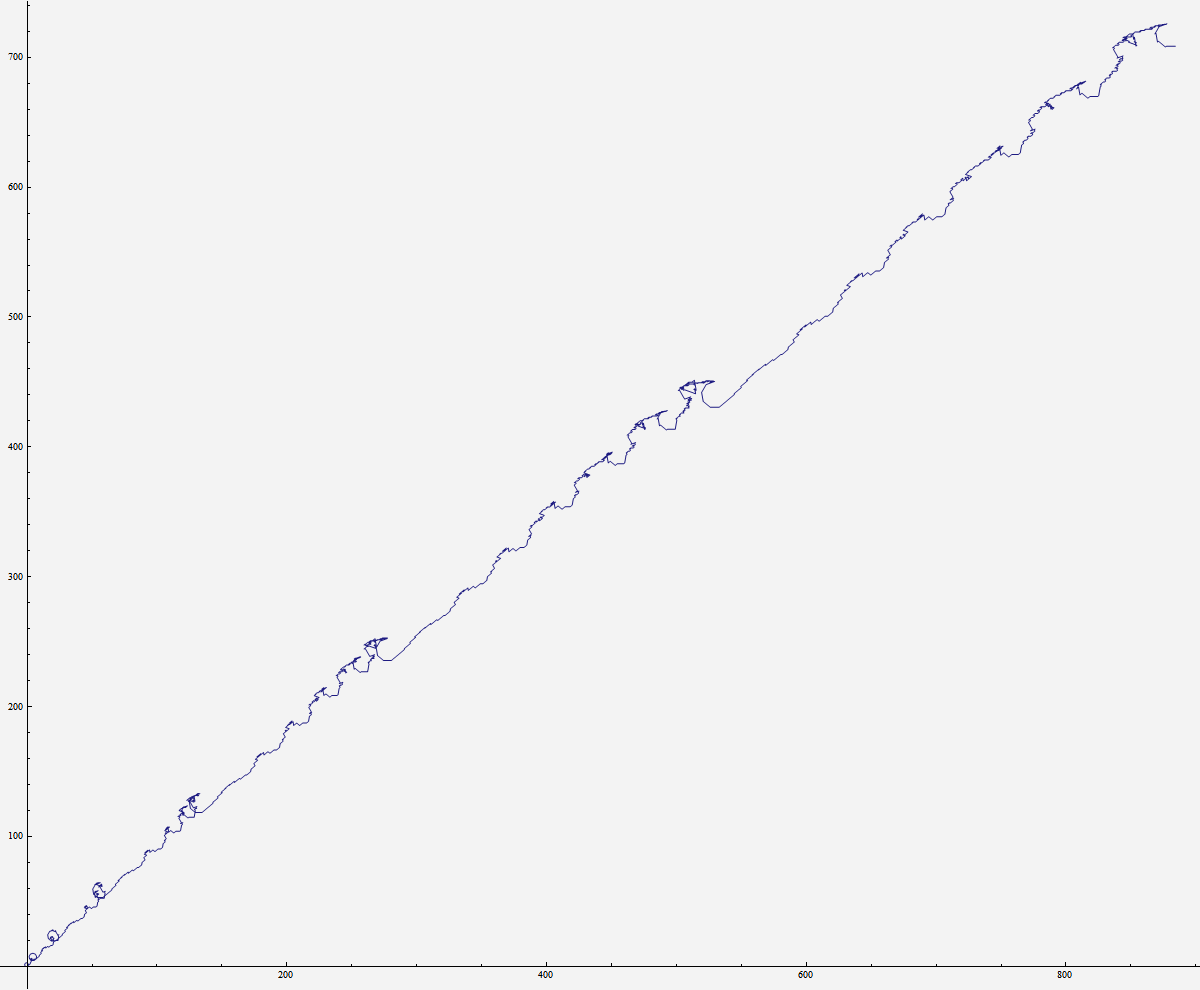
max1200

Magnifique, Jean-Marc, on voit bien ci-dessus le petit train de vagues qui monte et grossit !

Thanks to all contributors,

Best,

É.

P.-S. this is now http://oeis.org/A173646