PairWise Digit Sum
[English text published on SeqFans, on 6/15/2012 at 10:57 AM]:
Hello Seqfans (I hope this
idea is not old hat),
We change integer abcde...mn (with a,b,c,d,e,..m,n being digits) into integer a+b|b+c|c+d|d+e|e+...+m|m+n
(where the symbol < | means <
concatenate with . Then we iterate.
So 2012 gives 2+0|0+1|1+2 which is 213.
213 gives 2+1|1+3 which is 34.
And 34 gives 3+4 = 7 (which we call "end result")
1) What integers are divisible by their end result?
2) 991 loops -- as 992, 993, 994, 995, 996, 997, 998, 999 (ex. 991-1810-991...); which integers > 999 also
enter in a loop?
3) Which is the smallest integer growing for ever (if
such an integer exists)? I don't know the fate of 1891, for example:
1891-91710-10881-18169-99715-181686-9971414...
Besides, is
there an end pattern here: 1991
101810
11991
2101810
311991
42101810
6311991
942101810
Best, ...
É.
---------------------------------------------------
[Jack Brennen on Seqfans]:
After just 46 iterations, 1891 ends up with a number
with 115236 digits; I think it's a safe conjecture that it grows forever. There
is a pattern to it. At the 19th iteration, the number begins with:
18168554419171361118161213169411181614106781186648741118161412106774461411111055
And at the 20th iteration, the number begins with:
99714131098510108849722997733447151352299775516131592914121012151152299775533161
Afterward, the first digits cycle through those two
strings apparently ad infinitum.
I believe the
smallest starting number which seems to grow forever is 1496, which ends up at 1891 after four
iterations:
1496 -> 51315 -> 6446 -> 10810 -> 1891
-> ...
---------------------------------------------------
[Texte français
publié sur Fr.Sci.Maths quelques jours plus tard] :
Bonjour à tous,
Transformons l’entier N
composé des chiffres {abcde... mn} en l’entier M
ainsi:
M = {a+b|b+c|c+d|d+e|...
|m+n} où le symbole < | > veut dire < concaténé avec >.
On itère ensuite M en O,
puis O en P, etc.
Ainsi 178 devient-il 1+7|7+8
soit 815, lequel devient 8+1|1+5 soit 96, lequel produit 9+6 soit 15, qui fait
1+5 = 6, fin.
1) quel
est le plus petit entier qui générera une suite de nombres infinie ?
2)
quels autres entiers que 991, 992, 993, 994, 995, 996, 997, 998 et 999 bouclent
? On voit p.ex. que 991 produit 1810 qui reproduit
991.
Voici, pour le point (1) un motif intéressant à
croissance infinie trouvé par Jack
Brennen, que je cite :
For an interesting pattern which is obviously provable to be infinite,
start with 4949:
4949
131313
44444
8888
161616
77777
14141414
5555555
101010101010
11111111111
2222222222
444444444
88888888
etc.
à+
É.
---------------------------------------------------
[Acetonik] sur Fr.Sci.Maths :
[..]
de 1 à 1495 toutes les suites générées sont finies
ou infinies périodiques.
Les périodiques sont celles générées par les nombres
consécutifs :
de 991 à 999
de 1082 à 1089
de 1256 à 1259
de 1491 à 1495
Une étude exhaustive est facile et rapide jusqu’à 1495,
il faut calculer peu de termes pour chaque nombre.
Le plus petit nombre qui pourrait générer un une suite
non périodique infinie est 1496... Reste à le prouver !
(pour info, après 30
"concaténations" on obtient un nombre de 701 chiffres)
Donc :
1) quel est le plus petit entier qui générera une suite
de nombres infinie?
1496 (très forte probabilité)
2) quels autres entiers que 991, 992, 993, 994, 995,
996, 997, 998 et 999 bouclent?
Liste exhaustive des 249 nombres inférieurs à 10000
qui génèrent une "concaténation" périodique:
[ils ne se raréfient pas:
123/5000 ; 249/10000]
991, 992, 993, 994, 995, 996, 997, 998, 999, 1082,
1083, 1084, 1085, 1086, 1087, 1088, 1089, 1256, 1257, 1258, 1259, 1491, 1492,
1493, 1494, 1495, 1537, 1538, 1539, 1810, 1811, 1812, 1813, 1814, 1815, 1816,
1817, 1818, 2165, 2166, 2167, 2168, 2169, 2446, 2447, 2448, 2449, 2720, 2721, 2722,
2723, 2724, 2725, 2726, 2727, 2802, 2803, 2804, 2805, 2806, 2807, 2808, 2809,
2935, 2936, 3074, 3075, 3076, 3077, 3078, 3079, 3355, 3356, 3357, 3358, 3359,
3630, 3631, 3632, 3633, 3634, 3635, 3636, 3711, 3712, 3713, 3714, 3715, 3716, 3717,
3718, 3844, 3845, 3937, 3938, 3939, 3950, 4264, 4265, 4266, 4267, 4268, 4540,
4541, 4542, 4543, 4544, 4545, 4620, 4621, 4622, 4623, 4624, 4625, 4626, 4627,
4753, 4754, 4846, 4847, 4848, 4849, 4927, 5173, 5174, 5175, 5176, 5177, 5450, 5451,
5452, 5453, 5454, 5530, 5531, 5532, 5533, 5534, 5535, 5536, 5662, 5663, 5755,
5756, 5757, 5758, 5759, 5836, 5901, 5902, 5903, 5904, 5905, 5930, 5931, 6082,
6083, 6084, 6085, 6086, 6360, 6361, 6362, 6363, 6440, 6441, 6442, 6443, 6444, 6445,
6571, 6572, 6664, 6665, 6666, 6667, 6668, 6669, 6745, 6810, 6811, 6812, 6813,
6814, 6840, 7270, 7271, 7272, 7350, 7351, 7352, 7353, 7354, 7480, 7481, 7506,
7507, 7508, 7509, 7573, 7574, 7575, 7576, 7577, 7578, 7654, 7720, 7721, 7722, 7723,
7920, 8180, 8181, 8260, 8261, 8262, 8263, 8390, 8415, 8416, 8417, 8418, 8482,
8483, 8484, 8485, 8486, 8487, 8563, 8630, 8631, 8632, 9090, 9170, 9171, 9172,
9324, 9325, 9326, 9327, 9391, 9392, 9393, 9394, 9395, 9396, 9472, 9540, 9541.
---------------------------------------------------
[Éric A] :
Un autre aspect "boucle" qui me plaît est
celui des demi-lignes infinies (à droite) composées d’entiers K identiques.
Ainsi 3333... fait-il 6666... puis 121212... puis
3333...
[Acetonik] :
Par exemple comme celles qui débutent par
99999 .....
puis
1818181818.......
etc., générées en
particulier par les nombres suivants:
5980 ; 5981 ; 6890 ; 9990 à 9999.
Le seul intérêt que je vois ici ; c’est qu’il est
facile de démontrer que les suites sont infinies.
---------------------------------------------------
[Acetonik] :
Un nombre génère par cette
concaténation l’un des 3 types de suite :
F-> une suite finie (le
dernier terme a un seul chiffre)
P-> une suite périodique
(boucle)
i-> une suite infinie non
périodique (pas de boucle)
Les nombres avec de grands
chiffres génèrent plutôt des suites infinies.
Les nombres avec de petits
chiffres génèrent plutôt des suites finies.
Les nombres générant des
suites périodiques sont peu nombreux (123/5000)
Voici une classification
donnant le type de suite associée aux entiers inférieurs à 5000.
0 à 990
-> F
991 à 999 -> P
1000 à 1081 -> F
1082 à 1089 -> P
1090 à 1255 -> F
1256 à 1259 -> P
1260 à 1490 -> F
1491 à 1495 -> P
1496 à 1499 -> i
1537 à 1539 -> P
1540 à 1586 -> F
1587 à 1589 -> i
1590 à 1690 -> F
1691 à 1699 -> i
1700 à 1718 -> F
1719 -> i
1720 à 1728 -> F
1729 -> i
1730 à 1782 -> F
1783 à 1789 -> i
1789 à 1809 -> F
1810 à 1818 -> P
1819 -> i
1820 à 1866 -> F
1867 à 1869 -> i
1870 à 1954 -> F
1955 à 1959 -> i
1960 à 1963 -> F
1964 à 1989 -> i
1990 -> F
1991 à 1999 -> i
2000 à 2164 -> F
2165 à 2169 -> i
2170 à 2445 -> F
2446 à 2449 -> P
2450 à 2495 -> F
2496 à 2499 -> i
2500 à 2627 -> F
2628 à 2629 -> i
2630 à 2636 -> F
2637 à 2639 -> i
2640 à 2691 -> F
2692 à 2699 -> i
2700 à 2718 -> F
2719 -> i
2720 à 2727 -> P
2728 à 2729 -> i
2730 à 2768 -> F
2769 -> i
2770 à 2775 -> F
2776 à 2779 -> i
2780 à 2782 -> F
2783 à 2799 -> i
2800 à 2801 -> F
2802 à 2809 -> P
2810 à 2863 -> F
2864 à 2869 -> i
2870 à 2872 -> F
2873 à 2899 -> i
2900 à 2934 -> F
2935 à 2936 -> P
2937 à 2945 -> F
2946 à 2949 -> i
2950 à 2953 -> F
2954 à 2979 -> i
2980 à 2981 -> F
2982 à 2999 -> i
3000 à 3073 -> F
3074 à 3079 -> P
3080 à 3354 -> F
3355 à 3359 -> P
3360 à 3536 -> F
3537 à 3539 -> i
3540 à 3545 -> F
3546 à 3549 -> i
3550 à 3578 -> F
3579 -> i
3580 à 3627 -> F
3628 à 3629 -> i
3630 à 3636 -> P
3637 à 3639 -> i
3640 à 3677 -> F
3678 -> i
3679 à 3684 -> F
3685 à 3689 -> i
3690 à 3691 -> F
3692 à 3699 -> i
3700 à 3710 -> F
3711 à 3718 -> P
3719 -> i
3720 à 3768 -> F
3769 -> i
3770 à 3772 -> F
3773 à 3779 -> i
3780 à 3781 -> F
3782 à 3799 -> i
3800 à 3843 -> F
3844 à 3845 -> P
3846 à 3854 -> F
3855 à 3859 -> i
3860 à 3862 -> F
3863 à 3889 -> i
3890 -> F
3891 à 3899 -> i
3900 à 3936 -> F
3937 à 3939 -> P
3940 à 3945 -> F
3946 à 3949 -> i
3950 -> P
3951 à 3979 -> i
3980 -> P
3981 à 3999 -> i
4000 à 4263 -> F
4264 à 4268 -> P
4269 -> i
4270 à 4445 -> F
4446 à 4449 -> i
4450 à 4454 -> F
4455 à 4459 -> i
4460 à 4487 -> F
4488 à 4489 -> I
4490 à 4536 -> F
4537 à 4539 -> i
4540 à 4545 -> P
4546 à 4549 -> i
4550 à 4578 -> F
4579 -> i
4580 à 4586 -> F
4587 -> i
4588 à 4593 -> F
4594 à 4599 -> i
4600 à 4619 -> F
4620 à 4627 -> P
4628 à 4629 -> i
4630 à 4677 -> F
4678 à 4679 -> i
4680 à 4681 -> F
4682 à 4689 -> i
4690 -> F
4691 à 4699 -> i
4700 à 4718 -> F
4719 -> i
4720 à 4748 -> F
4749 -> i
4750 à 4752 -> F
4753 à 4754 -> P
4755 à 4763 -> F
4764 à 4769 -> i
4770 à 4471 -> F
4772 à 4799 -> i
4800 à 4845 -> F
4846 à 4849 -> P
4850 à 4854 -> F
4855 à 4899 -> i
4900 à 4936 -> F
4937 à 4999 -> i
---------------------------------------------------
[Philippe 92]
Un nombre génère par cette
concaténation l’un des 3 types de suite :
F-> une suite finie (le
dernier terme a un seul chiffre)
P -> une suite périodique
(boucle)
i -> une suite infinie non
périodique (pas de boucle)
... peut-être faut-il distinguer ici deux sortes de
suites infinies :
a) les "réplicateurs"
M qui au bout d’un nombre fini d’étapes produisent M|M
ou éventuellement un M|M|...|M fini
b) les autres, "chaotiques"...
Tout ce phénomène ressemble étrangement aux diverses
variantes de "jeu de la vie"
---------------------------------------------------
[Acetonik] :
Petite précision : si l’on ne considère que des
suites périodiques (strictement, et non à partir d’un certain rang) on ne
trouve pour les nombres inférieurs à 10 000 que 15 nombres générateurs !!!
9 suites de période 2:
991, 992, 993, 994, 995, 996, 997, 998, 999, 1810,
1811, 1812, 1813, 1814, 1815, 1816, 1817, 1818.
6 suites de période 3:
6664, 6665, 6666, 6667, 6668, 6669,
121210, 121211, 121212, 121213, 121214, 121215, 33331, 33332, 33333,
33334, 33335, 33336.
---------------------------------------------------
[Olivier
Miakinen] :
Bonjour,
Le 17/06/2012 21:20, Philippe 92 a écrit :
[...]
Un nombre génère par cette concaténation l’un des 3
types de suite :
F -> une suite finie ( le
dernier terme a un seul chiffre)
P -> une suite périodique (boucle)
i -> une suite infinie non périodique (pas de
boucle)
> peut être faut-il distinguer ici deux sortes de
suites infinies :
>
> les "réplicateurs" M qui au bout d’un nombre fini d’étapes
> produisent M|M ou
éventuellement un M|M|...|M fini
>
> les autres,
"chaotiques" ...
Crois-tu qu’il soit possible de prouver qu’il existe
vraiment des suites chaotiques ici ? Qui sait si, au contraire, on ne pourrait
pas montrer que chaque suite infinie, même si elle semble longtemps chaotique,
ne serait pas au bout du compte un « multi-réplicateur
» (du style M -> M|M|M|M|...|M) ?
---------------------------------------------------
[Acetonik] :
Un peu d’ordre quand même
dans ce chaos...
Voici les effectifs des
différents types par classes de 1000.
F -> suite finie (le dernier terme a un seul chiffre)
P -> suite
périodique (ou partir d’un certain rang) ->
boucle
i -> suite infinie
non périodique -> pas de boucle
classes | F |
i | P |
------------------------------
0 à 999
| 991 | 0 | 9
|
| |
| |
1000 à 1999 |
866 | 105 | 29 |
| |
| |
2000 à 2999 |
850 | 123 | 27 |
| |
| |
3000 à 3999 |
821 | 147 | 32 |
| |
| |
4000 à 4999 |
783 | 191 | 26 |
| |
| |
5000 à 5999 |
733 | 235 | 32 |
| |
| |
6000 à 6999 |
701 | 269 | 30 |
| |
| |
7000 à 7999 |
650 | 324 | 26 |
| |
| |
8000 à 8999 |
591 | 388 | 21 |
| |
| |
9000 à 9999 |
537 | 446 | 17 |
------------------------------
0 à 9999
| 7523 | 2228 | 249 |
------------------------------
------------------------------
10000 à 10999| 510 | 479 | 10 |
------------------------------
... et plus exactement, pour les nombres inférieurs à
10 000 on ne trouve que :
9 suites de période 2:
991, 992, 993, 994, 995, 996, 997, 998, 999, 1810,
1811, 1812, 1813, 1814, 1815, 1816, 1817, 1818.
6 suites de période 3:
6664, 6665, 6666, 6667, 6668, 6669,
121210, 121211, 121212, 121213, 121214, 121215, 33331, 33332, 33333,
33334, 33335, 33336.
Soit 24 nombres
générateurs de suites périodiques:
991, 992, 993, 994, 995, 996, 997, 998, 999, 1810,
1811, 1812, 1813, 1814, 1815, 1816, 1817, 1818, 6664, 6665, 6666, 6667, 6668,
6669.
---------------------------------------------------
[Lars Blomberg] :
Hello Eric,
Is this not the same problem as described in
http://www2.stetson.edu/~efriedma/mathmagic/0200.html
?
When investigating it, I recognized some of the results.
:-)
I found some
documentation that I made almost a year ago concerning this problem.
___________________________________________________________________________________________________________________
7 Pairwise Digit Sums and Concatenate
7.1 Problem definition
Erich Friedmann
introduces a "Problem of the Month" in February 2000 which Eric
Angelini revived recently in SeqFan, defined as
follows.
For integer n, let f(n) be the concatenation of the sums of every pair of
consecutive digits of n. For example, f(82671)=108138,
since 8+2=10, 2+6=8, 6+7=13, and 7+1=8. If n is a single digit, define f(n)=0.
See http://www2.stetson.edu/~efriedma/mathmagic/0200.html
for more information.
Several interesting questions can be
asked regarding this problem, some of which are answered on the above Web site.
Additional investigations are
presented in the following.
7.2 Some basics
Pairwise summing of
digits gives 1-digit sums in 55 cases (45 cases for the first pair in a number
since numbers do not start with 0):
00
01 10
02 11 20
03 12 21 30
04 13 22 31 40
05 14 23 32 41 50
06 15 24 33 42 51 60
07 16 25 34 43 52 61
70
08 17 26 35 44 53 62
71 80
09 18 27 36 45 54 63
72 81 90
And 2-digit sums in 45 cases
(first digit is always 1):
19 28 37 46 55 64 73
82 91
29 38 47 56 65 74 83
92
39 48 57 66 75 84 93
49 58 67 76 85 94
59 68 77 86 95
69 78 87 96
79 88 97
89 98
99
For a n-digit
number there are n-1 pairs to be summed. Each pair results in 1 or 2 digits.
Therefore the resulting number will have m digits, n-1≤m≤2(n-1).
For a number to become shorter,
all the pairwise sums need to be 1 digit. Obviously
the chance of this happening diminishes with the number of digits in the
number.
Given m, what is the range of n?
n-1≤m and m≤2(n-1)
n≤m+1
and floor(m/2)+1≤n so
floor(m/2)+1≤n≤m+1
If an n-digit number is
transformed into a m-digit number then there
have been t=m-n+1 pairs that have yielded a 2-digit result, 0≤t≤n-1.
When f(2056)
= 2511, we say that 2511 is the successor of 2056, and
conversely, 2056 is the predecessor of 2511.
All numbers have a successor.
Sometimes the successor iteration
leads to one value being repeated indefinitely as a fixed point, for example 0.
Other iterations lead to a set of
values being repeated in a cycle, for example 991 --> 1810 --> 991.
Yet other iterations lead to
numbers that grow in size indefinitely.
Some numbers have no predecessors,
for example 110.
Numbers can have many predecessors,
for example 9 <-- {18, 27, 36, 45, 54, 63, 72, 81, 90}.
7.3 Cycles
Some successor sequences lead into
cycles.
The following cycles have been
found by Joseph DeVincentis and others:
99(a+1) --> 181a
--> 99(a+1) [where 0≤a≤8]
3333(a+1) -->
666(a+4) --> 12121a --> 3333(a+1) [where 0≤a≤5]
or, more
explicitly:
L1 1810 --> 991
-->
L2 1811 --> 992
-->
L3 1812 --> 993
-->
L4 1813 --> 994
-->
L5 1814 --> 995
-->
L6 1815 --> 996
-->
L7 1816 --> 997
-->
L8 1817 --> 998
-->
L9 1818 --> 999
-->
M1 121210 --> 33331
--> 6664 -->
M2 121211 -->
33332 --> 6665 -->
M3 121212 -->
33333 --> 6666 -->
M4 121213 -->
33334 --> 6667 -->
M5 121214 -->
33335 --> 6668 -->
M6 121215 -->
33336 --> 6669 -->
There are 15 cycles containing a
total of 36 values.
7.4 Expanding cycles
Some iterations
do not terminate with 0 or one of the cycles, they go on forever.
Such iterations of course lead to
numbers that grow beyond limit.
Some (all?)
of these infinite iterations exhibit a cyclic pattern in the first few digits. When a cycle
is completed, at least one more digit has been added to the right, otherwise we
would have a proper cycle.
The additional digits for each
cycle make it an expanding cycle.
Of course, there might be more
digits to the right of the cycling numbers which may or may not expand by
themselves.
The following 24 expanding cycles
have been found, each has been given a name.
The information inside () are the
extra digits generated with each cycle. When the count of these digits exceeds
9, the count is instead given inside (<>).
A1 18141 -->
9955 --> 18141(0)
A2 18146 -->
9951(0) --> 18146(1)
A3 18151 -->
9966 --> 18151(2)
A4 18157 -->
9961(2) --> 18157(3)
A5 18161 -->
9977 --> 18161(4)
A6 18168 -->
9971(4) --> 18168(5)
A7 18171 -->
9988 --> 18171(6)
A8 18179 -->
9981(6) --> 18179(7)
A9 18181 -->
9999 --> 18181(8)
B1 66661 -->
1212127 --> 333339 --> 66661(2)
B2 66666 -->
1212121(2) --> 333333(3) --> 66666(6)
B3 66678 -->
1212131(5) --> 333344(6) --> 66678(10)
B4 66691 -->
1212151(0) --> 333366(1) --> 66691(27)
C1 18121 -->
9933 --> 18126 --> 9938 --> 18121(1)
C2 18124 -->
9936 --> 18129 --> 9931(1) --> 18124(2)
D1 18111 -->
9922 --> 18114 --> 9925 --> 18117 --> 9928 --> 18111(0)
D2 18113 -->
9924 --> 18116 --> 9927 --> 18119 --> 9921(0) --> 18113(1)
D3 18131 -->
9944 --> 18138 --> 9941(1) --> 18135(2) --> 9948(7) -->
18131(215)
E1 66642 -->
1212106 --> 333316 --> 66647 --> 1212101(1) --> 333311(2) -->
66642(3)
E2 66681 --> 1212149 --> 333351(3) --> 66686(4)
--> 1212141(410) --> 333355(551) --> 66681(010106)
F 222222 --> 44444 --> 8888 --> 161616 -->
77777 --> 14141414 --> 5555555 --> 101010101010 --> 11111111111
--> 222222(2222)
G 66651 --> 1212116 --> 333327 --> 66659
--> 1212111(4) --> 333322(5) --> 66654(7) --> 1212119(11) -->
333321(0102) --> 66653(1112) --> 1212118(4223) --> 333329(12645)
--> 66651(11038109)
H 18101 --> 9911 --> 18102 --> 9912 -->
18103 --> 9913 --> 18104 --> 9914 --> 18105 --> 9915 -->
18106 --> 9916 --> 18107 --> 9917 --> 18108 --> 9918 -->
18109 --> 9919 --> 18101(0)
I 101088 --> 111816 --> 22997 --> 411181(6)
--> 52299(7) --> 741118(16) --> 115229(97) --> 26741(11816) -->
813115(22997) --> 94426(74111816) --> 13868(<10>) -->
411141(<14>) --> 52255(<18>) --> 74710(<25>) --> 111181(<30>)
--> 22299(<40>) --> 441118(<50>) --> 85229(<68>)
--> 137411(<82>) --> 4101152(<112>) -->
511267(<141>) --> 62381(<188>) --> 85119(<241>) -->
13621(<318>) --> 4983(<403>) --> 13171(<532>) -->
4488(<680>) --> 81216(<881>) --> 9337(<1123>) -->
12610(<1453>) --> 3871(<1865>) --> 11158(<2407>) -->
22613(<3078>) --> 4874(<3961>) --> 121511(<5108>)
--> 33662(<6540>) --> 69128(<8454>) -->
151031(<10813>) --> 66134(<14019>) --> 12747(<17945>)
--> 391111(<23196>) --> 1210222(<29697>) -->
331244(<38401>) --> 64368(<49279>) --> 10791(<63825>)
--> 17161(<81773>) --> 8877(<105797>) -->
16151(<135743>) --> 7766(<175542>) --> 141312(<225282>)
--> 55443(<291102>) --> 10987(<373857>) -->
19171(<483295>) --> 101088(<620681>)
The number of iterations until the
cycle is closed is
|
A1 |
2 |
|
A2 |
2 |
|
A3 |
2 |
|
A4 |
2 |
|
A5 |
2 |
|
A6 |
2 |
|
A7 |
2 |
|
A8 |
2 |
|
A9 |
2 |
|
B1 |
3 |
|
B2 |
3 |
|
B3 |
3 |
|
B4 |
3 |
|
C1 |
4 |
|
C2 |
4 |
|
D1 |
6 |
|
D2 |
6 |
|
D3 |
6 |
|
E1 |
6 |
|
E2 |
6 |
|
F |
9 |
|
G |
12 |
|
H |
18 |
|
I |
53 |
Berend Jan van der Zwaag states 23 expanding cycles, he forgot to mention A3
(the value 9966 in his enumeration).
7.5 Successor statistics
Given a number, the successor
iteration ends up in 0, one of the cycles (LM), or one of the expanding cycles
(A-I).
For all numbers up to 10^6 the
outcome has been determined for the 10 intervals of size 10^5 resulting in the
following table:
|
Interval |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
ZERO |
20822 |
1475 |
1288 |
1064 |
918 |
781 |
637 |
548 |
447 |
320 |
|
L1 |
23 |
1 |
0 |
2 |
0 |
1 |
1 |
1 |
1 |
0 |
|
L2 |
27 |
1 |
0 |
2 |
0 |
1 |
1 |
0 |
1 |
1 |
|
L3 |
33 |
1 |
0 |
2 |
0 |
1 |
1 |
0 |
1 |
1 |
|
L4 |
60 |
3 |
1 |
3 |
0 |
3 |
2 |
0 |
2 |
1 |
|
L5 |
71 |
4 |
5 |
2 |
1 |
3 |
0 |
0 |
2 |
2 |
|
L6 |
81 |
4 |
4 |
4 |
2 |
4 |
0 |
0 |
2 |
2 |
|
L7 |
106 |
8 |
8 |
7 |
7 |
5 |
1 |
0 |
4 |
2 |
|
L8 |
79 |
4 |
6 |
3 |
4 |
4 |
1 |
1 |
0 |
1 |
|
L9 |
19 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
M1 |
19 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
M2 |
20 |
1 |
2 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
M3 |
21 |
2 |
2 |
2 |
1 |
0 |
1 |
0 |
1 |
0 |
|
M4 |
22 |
2 |
3 |
2 |
2 |
0 |
1 |
0 |
1 |
0 |
|
M5 |
30 |
3 |
4 |
2 |
2 |
2 |
1 |
0 |
1 |
0 |
|
M6 |
29 |
3 |
2 |
3 |
2 |
2 |
2 |
0 |
1 |
0 |
|
A1 |
9753 |
12964 |
11447 |
11849 |
10948 |
10176 |
11331 |
12278 |
13125 |
12828 |
|
A2 |
293 |
390 |
455 |
480 |
457 |
398 |
305 |
230 |
123 |
602 |
|
A3 |
858 |
1288 |
1247 |
1208 |
970 |
962 |
1221 |
882 |
873 |
1466 |
|
A4 |
2633 |
3438 |
3403 |
3901 |
4248 |
4740 |
3408 |
2693 |
2901 |
2668 |
|
A5 |
13599 |
17598 |
15508 |
16018 |
14980 |
16854 |
16515 |
18464 |
19115 |
16617 |
|
A6 |
735 |
833 |
612 |
747 |
901 |
1109 |
916 |
896 |
750 |
1038 |
|
A7 |
1785 |
3214 |
1907 |
2478 |
3243 |
2410 |
2138 |
1861 |
1955 |
2712 |
|
A8 |
59 |
94 |
64 |
58 |
43 |
43 |
30 |
31 |
20 |
210 |
|
A9 |
968 |
1306 |
1420 |
1185 |
1235 |
1331 |
1042 |
1085 |
1055 |
1661 |
|
B1 |
464 |
591 |
526 |
540 |
533 |
582 |
684 |
807 |
705 |
588 |
|
B2 |
561 |
279 |
299 |
401 |
403 |
349 |
901 |
985 |
1127 |
1086 |
|
B3 |
70 |
41 |
48 |
66 |
144 |
124 |
121 |
120 |
120 |
120 |
|
B4 |
115 |
112 |
135 |
146 |
193 |
168 |
232 |
286 |
240 |
202 |
|
C1 |
12112 |
15739 |
16582 |
14827 |
14048 |
14516 |
15655 |
15793 |
17271 |
16787 |
|
C2 |
100 |
162 |
147 |
122 |
26 |
34 |
43 |
30 |
41 |
445 |
|
D1 |
172 |
213 |
245 |
172 |
107 |
85 |
12 |
75 |
69 |
759 |
|
D2 |
103 |
198 |
159 |
107 |
58 |
69 |
41 |
55 |
51 |
362 |
|
D3 |
2145 |
1989 |
2233 |
2730 |
2475 |
2634 |
3272 |
3753 |
1731 |
2549 |
|
E1 |
130 |
124 |
131 |
205 |
125 |
129 |
218 |
206 |
189 |
195 |
|
E2 |
50 |
30 |
40 |
30 |
30 |
140 |
142 |
133 |
110 |
100 |
|
F |
2609 |
2092 |
2765 |
3385 |
3919 |
2963 |
2782 |
3265 |
4431 |
4794 |
|
G |
70 |
20 |
20 |
120 |
120 |
120 |
120 |
110 |
100 |
100 |
|
H |
842 |
622 |
608 |
729 |
703 |
692 |
750 |
898 |
960 |
2162 |
|
I |
28311 |
35149 |
38672 |
37396 |
39149 |
38563 |
37469 |
34514 |
32474 |
29619 |
The count of numbers ending in
each cycle and expanding cycle varies greatly.
Zeros decrease as numbers
increase.
Cycles are scarce overall and seem
to get scarcer as the numbers increase.
All iterations that go off to
infinity are one of the expanding cycles. No iteration with "random"
digit pattern has been found for numbers < 10^6.
This suggests a few challenges:
1) Prove that the cycles L-M are the only possible
ones.
2) Prove that the expanding cycles A-I are the only
possible ones.
3) Is there a number above which no number goes to 0?
7.6 Predecessor statistics
There are 165 numbers < 10^3
with no predecessor:
110
120
121
130
131
132
...
The requirement is that the middle
digit is at least as big as the sum of the other two (Berend
Jan van der Zwaag).
Using an algorithm that determines
all predecessors to a given number, we get the following table.
|
Up to -> |
10^3 |
10^4 |
10^5 |
10^6 |
10^7 |
10^8 |
10^9 |
10^10 |
|
0 |
165 |
2867 |
42907 |
548144 |
6520193 |
73543012 |
801726786 |
8528432789 |
|
1 |
164 |
1915 |
19359 |
181374 |
1595745 |
13495392 |
110380431 |
881047611 |
|
2 |
164 |
1668 |
14622 |
122298 |
961085 |
7283293 |
53447981 |
383324517 |
|
3 |
158 |
1378 |
10570 |
76789 |
528707 |
3527594 |
22879751 |
145514909 |
|
4 |
121 |
929 |
6269 |
40189 |
243655 |
1432601 |
8187936 |
45923129 |
|
5 |
89 |
591 |
3446 |
19090 |
100242 |
511013 |
2536968 |
12372762 |
|
6 |
62 |
348 |
1716 |
8081 |
36128 |
157222 |
667483 |
2789252 |
|
7 |
40 |
184 |
748 |
2929 |
10946 |
40031 |
143455 |
508212 |
|
8 |
23 |
83 |
271 |
866 |
2683 |
8229 |
24994 |
75694 |
|
9 |
11 |
29 |
76 |
199 |
525 |
1390 |
3701 |
9892 |
|
10 |
2 |
7 |
15 |
40 |
90 |
222 |
513 |
1233 |
|
Sum |
999 |
9999 |
99999 |
999999 |
9999999 |
99999999 |
999999999 |
9999999999 |
(ex. “Up to 10^4 there are 1668 integers with 2 predecessors”)
Numbers with no predecessors
become more frequent as numbers grow larger, whereas ones with 1..10 predecessors seem to reach a maximum and then recede as
illustrated graphically below.
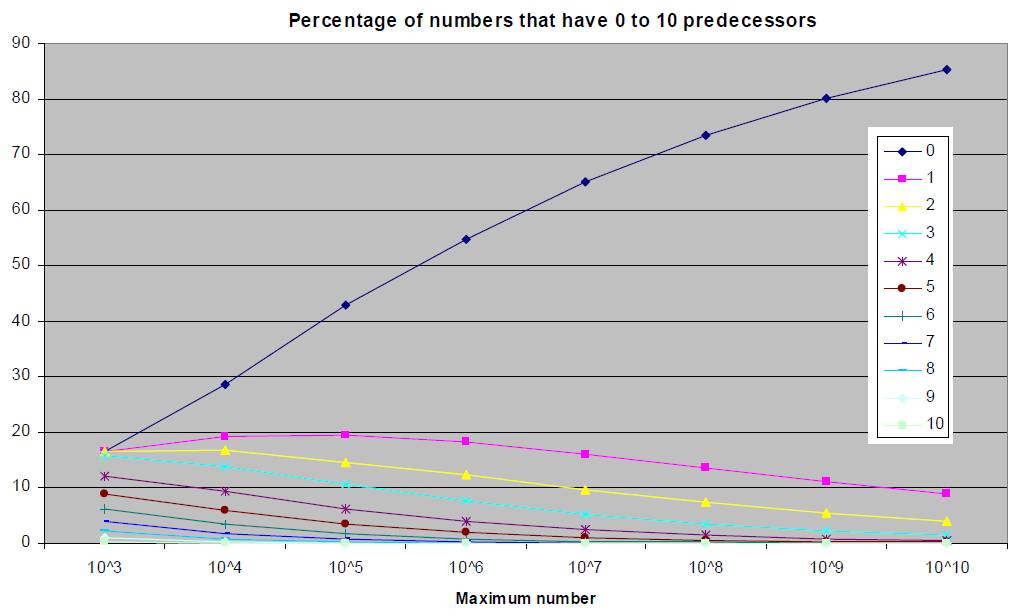
What is surprising is that no
number (below 10^10) has more than 10 predecessors. (The reverse algorithm used
here is more complicated but requires less time and memory than using the
forward algorithm for this purpose. The data in the above diagram up to 10^8
has been verified by using the forward algorithm.)
More predecessors maybe will appear
for numbers larger than 10^10.
Using 10^7 random samples each of
numbers up to 30 digits, the following graph was obtained.
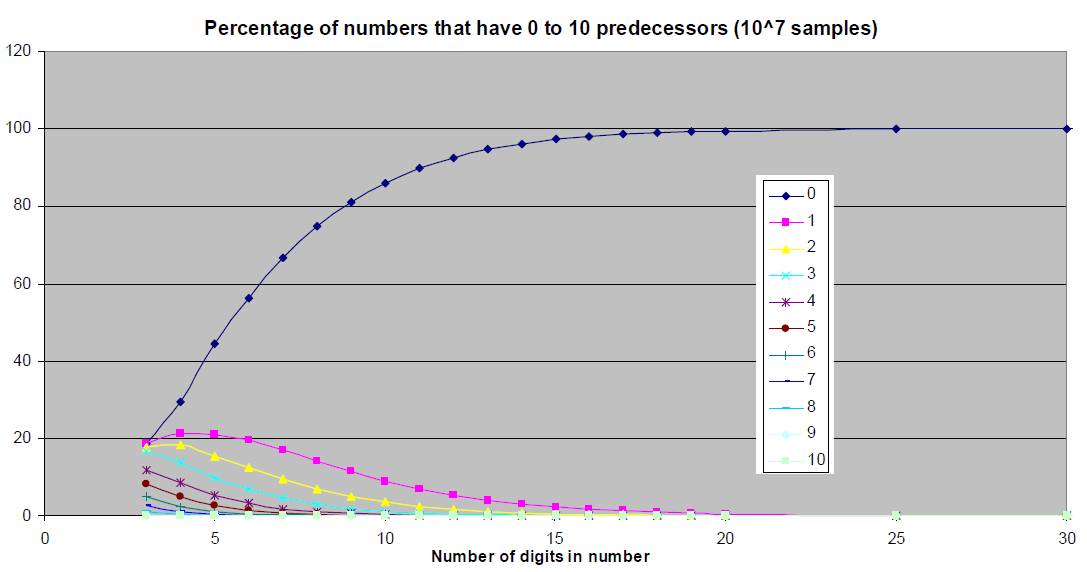
This diagram is similar to the
previous one.
No number with more that 10 predecessors was found, but it may be that 11 or
more is extremely rare and needs a very large number of digits.
So there are two more challenges:
4) Find a number that has 11 or more predecessors, or
5) Prove that no number can have more than 10
predecessors.
7.7 Numbers with 10 predecessors
Numbers with 10 predecessors has
been calculated for all numbers < 10^10 (see previous section).
The count of occurrences numbers
less than different powers of 10 is:
|
10^3 |
10^4 |
10^5 |
10^6 |
10^7 |
10^8 |
10^9 |
10^10 |
|
2 |
7 |
15 |
40 |
90 |
222 |
513 |
1233 |
A few of the first entries are
Number ... Predecessors ...
|
10 |
100 |
19 |
28 |
37 |
46 |
55 |
64 |
73 |
82 |
91 |
|
109 |
1009 |
190 |
281 |
372 |
463 |
554 |
645 |
736 |
827 |
918 |
|
1010 |
191 |
282 |
373 |
464 |
555 |
646 |
737 |
828 |
9100 |
919 |
|
1011 |
10010 |
192 |
283 |
374 |
465 |
556 |
647 |
738 |
829 |
9101 |
|
1099 |
10090 |
1909 |
2818 |
3727 |
4636 |
5545 |
6454 |
7363 |
8272 |
9181 |
|
1110 |
10100 |
1019 |
291 |
382 |
473 |
564 |
655 |
746 |
837 |
928 |
|
9910 |
18100 |
1819 |
2728 |
3637 |
4546 |
5455 |
6364 |
7273 |
8182 |
9091 |
|
10109 |
1918 |
2827 |
3736 |
4645 |
5554 |
6463 |
7372 |
8281 |
91009 |
9190 |
|
10119 |
100109 |
1927 |
2836 |
3745 |
4654 |
5563 |
6472 |
7381 |
8290 |
91018 |
|
10910 |
10091 |
28100 |
2819 |
3728 |
4637 |
5546 |
6455 |
7364 |
8273 |
9182 |
|
10911 |
10092 |
19010 |
28101 |
3729 |
4638 |
5547 |
6456 |
7365 |
8274 |
9183 |
|
10999 |
100909 |
19090 |
28181 |
37272 |
46363 |
55454 |
64545 |
73636 |
82727 |
91818 |
|
11109 |
101009 |
10190 |
2918 |
3827 |
4736 |
5645 |
6554 |
7463 |
8372 |
9281 |
|
98910 |
18091 |
27182 |
36273 |
45364 |
54455 |
63546 |
72637 |
81728 |
908100 |
90819 |
|
99109 |
181009 |
18190 |
27281 |
36372 |
45463 |
54554 |
63645 |
72736 |
81827 |
90918 |
From this and from the complete
data set in the file Pred10.txt one can see some recurring patterns.
Maybe these patterns are a clue to
solving the 10-predecessor problem.
A few more observations:
o Numbers start with 1 or 9.
o Numbers contain only digits 0, 1,
2, 8, 9, therefore no number contains any of the digits 3-7.
o Last digit is 0, 1 or 9.
o Last two digits are 09, 10, 11, 19
or 99.
(c) Lars Blomberg
___________________________________________________________________________________________________________________
Thanks to all, merci à tous !