Weighing scales and
sequences

Hello SeqFans,
Here is a first
succession of empty weighing scales:
|††† †|†
|†††† |† |††††
|† |†††† |†
|†††† |† |††††
|† |†††† |†
|†††† |† |†††† |
+--.--+† +--.--+†
+--.--+† +--.--+† +--.--+†
+--.--+† +--.--+† +--.--+†
+--.--+
We write under each
scale its (un)balance:
|†††† |†
|†††† |† |††††
|† |†††† |†
|†††† |† |†††† |† |††††
|† |†††† |†
|†††† |
+--.--+† +--.--+†
+--.--+† +--.--+† +--.--+†
+--.--+† +--.--+† +--.--+†
+--.--+
†† 0†††††††
0†††††††
0†††††††
0†††††††
0†††††††
0†††††††
0†††††††
0†††††††
0††
We fill each scale
with two integer weights:
|1†† 2|† |3††
5|† |6 ††9|† |10
15|† |16 22|† |23 32|†
|33 43|† |44 59|† |60 76|
+--.--+† +--.--+†
+--.--+† +--.--+† +--.--+†
+--.--+† +--.--+† +--.--+†
+--.--+
†† 1†††††††
2††††††† 3††††††† 5†††††††
6††††††† 9††††††† 10††††††
15†††††† 16††
Ok, you get it, the
unbalancesí seq is the seq
formed by the successive weights:
S = 1,2,3,5,6,9,10,15,16,22,23,32,33,43,44,59,60,76,...
S is monotonically increasing and not in the OEIS.
If we drop the
"monotonically increasing" constraint and want the sequence to be a
permutation of the Natural numbers (1,2,3,4,5,6,7,...n)
we have:
T =
1,2,3,5,4,7,6,11,8,12,9,16,13,19,10,21,14,22,15,27,17,26,18,34,20,33,23,42,25,35,24,45,29,43,28,50,...
The algorithm used
here was, as usual, "take the smallest available integer not yet present
in T and not
leading to a contradiction". T is not in the OEIS either.
Building T is smooth -- except for
some weights which have to be delayed:
T = 1,2,3,5,4,7,6,11,8,12,9,16,13,19,
... is ok
†††† 1††
2†† 3†† 5†††
4††† 7†††† 6
T = 1,2,3,5,4,7,6,11,8,12,9,16,10,--, ... is not (10-6
and 10+6 are already in T)
†††† 1††
2†† 3†† 5†††
4††† 7†††† 6
Now, what happens
_between_ the weighing scales?
For S, the scales are always
"separated" by weights of 1 unit:
S = |1†† 2|†† |3††
5| ††|6†† 9|††
|10 15|†† |16 22|†† |23 32|††
|33 43|†† |44 59|†† |60 76|
††† +--.--+ 1 +--.--+ 1 +--.--+ 1 +--.--+ 1
+--.--+ 1 +--.--+ 1 +--.--+ 1 +--.--+ 1 +--.--+
†††††† 1†††
^††† 2††† ^†††
3††† ^††† 5†††
^††† 6††† ^†††
9††† ^††† 10††
^††† 15†† ^†††
16††
Could the succession
of the separations be the sequence itself? Letís try:
Sí = |1†† 2|†† |3††
5|†† |7† 10|††
|13 18|†† |23 30|†† |37 47|†††
|57 70|††† |83† 101|††
†††† +--.--+ 1 +--.--+ 2 +--.--+ 3 +--.--+ 5
+--.--+ 7 +--.--+ 10 +--.--+ 13 +---.---+† ...
††††††† 1†††
^††† 2††† ^†††
3††† ^††† 5†††
^††† 7††† ^†††
10†† ^^††† 13††
^^†††† 18††††††††
It works... but Sí is already in the OEIS: http://www.research.att.com/~njas/sequences/A033485
with the
definition: "a(n) = a(n-1) + a([n/2]), a(1) = 1"
Now the difficult
part: could we build a sequence similar to S, but dropping the "monotonically increasing"
constraint?
We are thus looking
for a sequence Tí
where:
- a(n)
is not always > a(n-1)
- a(n)
doesnít show twice
- the succession of
the separations (between successive scales) form Tí itself
I think Tí is not impossible to
construct and might start like this:
Tí = |1†† 2|††
|3†† 5|†† |7† 10|††
|13 18|†† |23 16|†† |9†
19|††† |29 42|††† |55 37|††
†††† +--.--+ 1 +--.--+ 2 +--.--+ 3 +--.--+ 5
+--.--+ 7 +--.--+ 10 +--.--+ 13 +--.--+† ...
††††††† 1†††
^††† 2††† ^†††
3††† ^††† 5†††
^††† 7††† ^†††
10†† ^^††† 13††
^^††† 18††††††††
Could Tí be a permutation of
the Naturals? Mmmmmh...
Best,
….
__________
[Douglas McNeil, a couple of hours later, June 14th,
2010]:
I believe I can
confirm your values for the easier sequences S, T, and Sí:
sage:
S[:50]
[1,
2, 3, 5, 6, 9, 10, 15, 16, 22, 23, 32, 33, 43, 44, 59, 60, 76, 77, 99, 100,
123, 124, 156, 157, 190, 191, 234, 235, 279, 280, 339, 340, 400, 401, 477, 478,
555, 556, 655, 656, 756, 757, 880, 881, 1005, 1006, 1162, 1163, 1320]
sage:
T[:50]
[1,
2, 3, 5, 4, 7, 6, 11, 8, 12, 9, 16, 13, 19, 10, 21, 14, 22, 15, 27, 17, 26, 18,
34, 20, 33, 23, 42, 25, 35, 24, 45, 29, 43, 28, 50, 31, 46, 30, 57, 32, 49, 36,
62, 37, 55, 38, 72, 39, 59]
sage:
Sí[:50]
[1, 2, 3, 5, 7, 10,
13, 18, 23, 30, 37, 47, 57, 70, 83, 101, 119, 142, 165, 195, 225, 262, 299,
346, 393, 450, 507, 577, 647, 730, 813, 914, 1015, 1134, 1253, 1395, 1537,
1702, 1867, 2062, 2257, 2482, 2707, 2969, 3231, 3530, 3829, 4175, 4521, 4914]
But I disagree with
the last value of Tí,
37: I think the pair (55,37) blocks and you have to
use 73.
sage: Tí[:50]
[1, 2, 3, 5, 7, 10,
13, 18, 23, 16, 9, 19, 29, 42, 55, 73, 91, 68, 45, 61, 77, 86, 95, 114, 133,
104, 75, 117, 159, 214, 269, 342, 415, 324, 233, 165, 97, 142, 187, 248, 309,
232, 155, 241, 327, 422, 517, 631, 745, 612]
Doug
__________
[me,
Eric]:
Thank you, Doug!
> But I
disagree with the last value of Tí, 37:
... yes, you are right, I was not careful enough, thanks!
Best,
….
__________
[February 2014
update]
I had forgotten about
this page in February 2014 Ė and reposted on SeqFans the same question (about T) -- in other words
(shame on me!):
Hello SeqFans,
Here is a permutation of the Naturals not yet in the OEIS,
I think:
T=1,2,3,5,4,7,6,11,8,12,9,16,13,19,10,21,14,22,15,27,17,26,18,34,20,33,23,42,25,35,24,45,...
Put parentheses around each pair of integers, like this:
T=(1,2),(3,5),(4,7),(6,11),(8,12),(9,16),(13,19),(10,21),(14,22),(15,27),(17,26),(18,34),(20,33),(23,42),(25,35),(24,45),...
If you replace each pair of integers by their
difference, you'll get T
again:
T=1,2,3,5,4,7,6,11,8,12,9,16,13,19,10,21,14,22,15,27,17,26,18,34,20,33,23,42,25,35,24,45,...
T was
always extended with the smallest unused term not leading to a contradiction.
For example, after:
T=(1,2),(3,5),(4,7),(6,11),(8,12),(9,16),...
... one cannot extend T with 10 as 10 would
produce the pair (10,16) with a "16" being already used.
... similarly, after:
T=(1,2),(3,5),(4,7),(6,11),(8,12),(9,16),(13,19),(10,21),(14,22),(15,27),(17,26),(18,34),(20,33),(23,42),...
... one cannot extend T with 24 as 24 would produce the pair
(24,34) with a "34" being already used.
Best,
….
__________
Here is Jean-Marc Falcozí answer to this post, which
came together with 3 graphs of T (the 4th
and last one comes from Hans Havermann):
T = 1, 2, 3, 5, 4,
7, 6, 11, 8, 12, 9, 16, 13, 19, 10, 21, 14, 22, 15, 27, 17, 26, 18, 34, 20, 33,
23, 42, 25, 35, 24, 45, 29, 43, 28, 50, 31, 46, 30, 57, 32, 49, 36, 62, 37, 55,
38, 72, 39, 59, 40, 73, 41, 64, 44, 86, 51, 76, 47, 82, 53, 77, 48, 93, 52, 81,
54, 97, 56, 84, 58, 108, 60, 91, 61, 107, 65, 95, 63, 120, 66, 98, 67, 116, 68,
104, 69, 131, 74, 111, 70, 125, 71, 109, 75, 147, 78, 117, 79, 138, 83, 123,
80, 153, 85, 126, 87, 151, 88, 132, 89, 175, 90, 141, 92, 168, 96, 143, 94,
176, 99, 152, 100, 177, 101, 149, 102, 195, 103, 155, 105, 186, 106, 160, 110,
207, 113, 169, 112, 196, 114, 172, 115, 223, 118, 178, 119, 210, 121, 182, 122,
229, 124, 189, 127, 222, 128, 191, 129, 249, 133, 199, 130, 228, 134, 201, 135,
251, 136, 204, 137, 241, 139, 208, 140, 271, 142, 216, 144, 255, 145, 215, 148,
273, 146, 217, 150, 259, 156, 231, 154, 301, 157, 235, 158, 275, 159, 238, 161,
299, 162, 245, 163, 286, 164, 244, 165, 318, 167, 252, 166, 292, 170, 257, 171,
322, 173, 261, 174, 306, 179, 268, 180, 355, 184, 274, 183, 324, 185, 277, 181,
349, 187, 283, 188, 331, 190, 284, 192, 368, 194, 293, 193, 345, 197, 297, 198,
375, 202, 303, 203, 352, 200, 302, 205, 400, 206, 309, 209, 364, 211, 316, 212,
398, 213, 319, 214, 374, 218, 328, 219, 426, 220, 333, 221, 390, 224, 336, 225,
421, 226, 340, 227, 399, 232, 347, 230, 453, 233, 351, 234, 412, 237, 356, 236,
446, 239, 360, 240, 422, 243, 365, 242, 471, 246, 370, 247, 436, 250, 377, 248,
470, 253, 381, 254, 445, 256, 385, 258, 507, 260, 393, 262, 461, 264, 394, 263,
491, 267, 401, 265, 466, 269, 404, 266, 517, 270, 406, 272, 476, 276, 413, 278,
519, 279, 418, 280, 488, 285, 425, 281, 552, 282, 424, 287, 503, 288, 432, 289,
544, 290, 435, 291, 506, 294, 442, 295, 568, 298, 444, 296, 513, 300, 450, 304,
563, 307, 463, 305, 536, 308, 462, 310, 611, 311, 468, 312, 547, 314, 472, 313,
588, 315, 474, 317, 555, 320, 481, 321, 620, 323, 485, 325, 570, 326, 489, 327,
613, 329, 493, 330, 574, 332, 497, 334, 652, 335, 502, 337, 589, 338, 504, 339,
631, 341, 511, 342, 599, 343, 514, 344, 666, 348, 521, 346, 607, 350, 524, 353,
659, 354, 533, 357, 625, 358, 538, 359, 714, 361, 545, 362, 636, 363, 546, 366,
690, 369, 554, 367, 644, 372, 553, 371, 720, 373, 560, 378, 661, 376, 564, 379,
710, 382, 572, 380, 664, 383, 575, 384, 752, 386, 580, 387, 680, 388, 581, 389,
734, 395, 592, 391, 688, 392, 590, 396, 771, 402, 604, 397, 700, 403, 606, 405,
757, 408, 608, 407, 709, 409, 614, 410, 810, 411, 617, 414, 723, 415, 624, 416,
780, 417, 628, 419, 735, 420, 632, 423, 821, 427, 640, 428, 747, 429, 643, 430,
804, 431, 649, 433, 761, 434, 653, 437, 863, 438, 658, 439, 772, 441, 662, 440,
830, 443, 667, 447, 783, 448, 673, 449, 870, 451, 677, 452, 792, 454, 681, 455,
854, 457, 689, 456, 803, 464, 694, 458, 911, 459, 692, 460, 811, 465, 699, 467,
879, 469, 706, 473, 829, 475, 711, 477, 923, 478, 717, 479, 839, 482, 722, 480,
902, 483, 726, 484, 849, 486, 728, 487, 958, 490, 736, 492, 862, 494, 741, 495,
931, 496, 746, 498, 875, 500, 748, 499, 969, 501, 754, 505, 886, 508, 762, 509,
954, 510, 766, 512, 897, 515, 773, 516, 1023,...
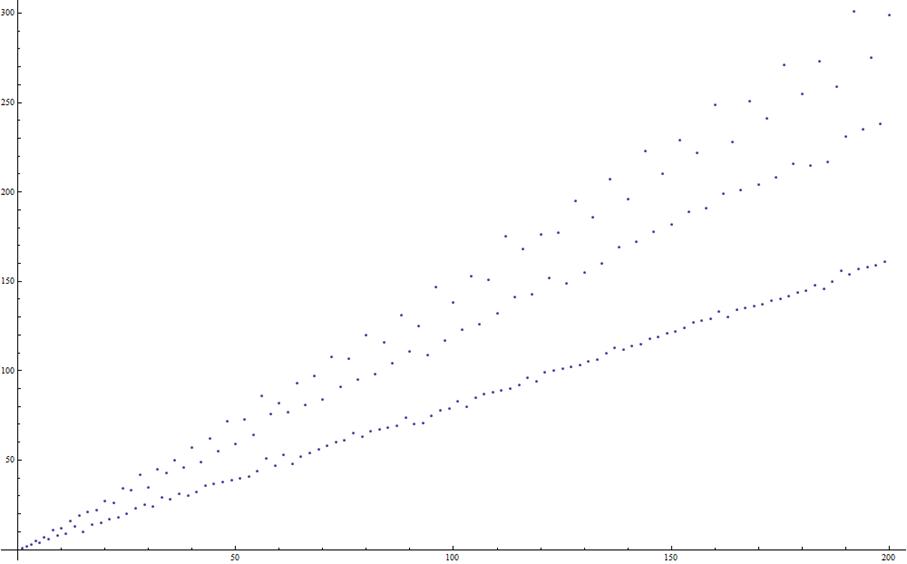
[100 terms
of T]
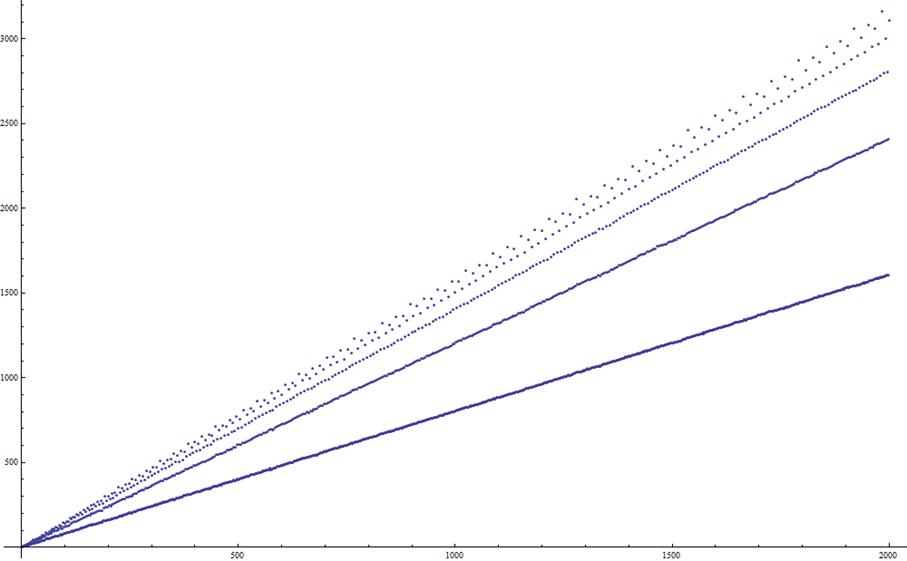
[1000
terms of T]
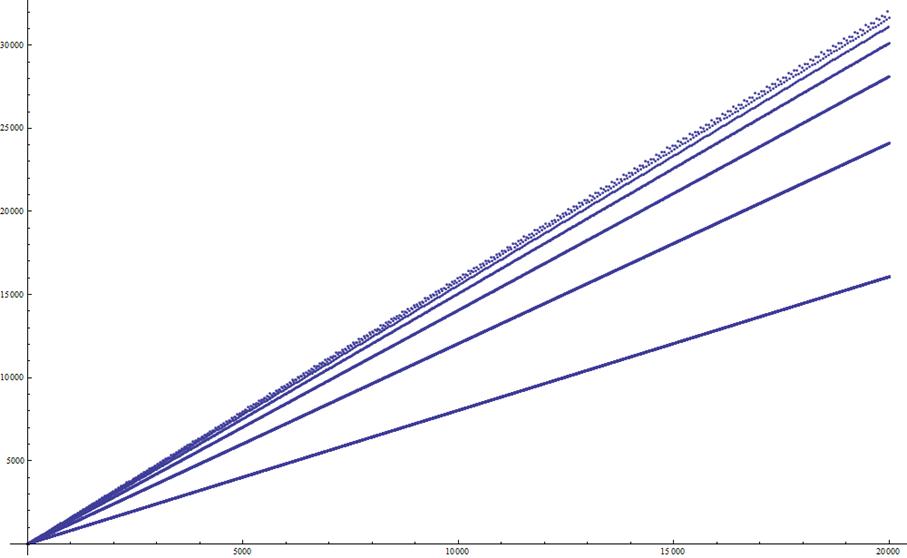
[10000
terms of T]
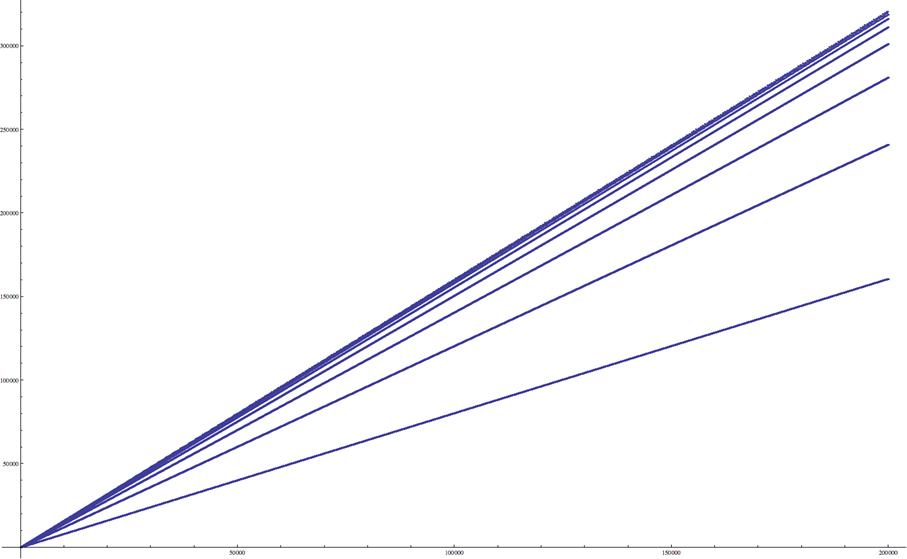
[20000
terms of T]
Many thanks to both
of you, Jean-Marc and Hans!
(and
sorry for the double take Ė but you know, getting old is dealing with horrible memory
problems! Ė Worse, Iíve recently discovered that Iím having problems with my
short term memory and my short term memory!-)