Smallest digit makes the difference

Hello SeqFans,

Underline the smallest digit of any a(n) in the sequence U. Now a(n+1) is the smallest integer not occurring earlier that has two digits separated by the underlined digit. Starting U with a(1)=1 should give:

This is great fun to do by hand – but you know, typos, autocorrect, memory loss, etc.

[and indeed, Hans Havermann found a typo on January 14^th, 2014 – now corrected above]

Best,

É.

__________

Explanation:

Why is a(2) equal to 10? Because 10 is the smallest unused integer that has two digits (1 and 0) separated by the smallest digit of the previous term (1);

Why is a(3) equal to 11? Because 11 is the smallest unused integer that has two digits (1 and 1) separated by the smallest digit of the previous term (0, present in ‘10’);

Why is a(4) equal to 12? Because 12 is the smallest unused integer that has two digits (1 and 2) separated by the smallest digit of the previous term (1, present in ‘11’);

Why is a(5) equal to 21? Because 21 is the smallest unused integer that has two digits (2 and 1) separated by the smallest digit of the previous term (1, present in ‘12’);

Why is a(6) equal to 23? Because 23 is the smallest unused integer that has two digits (2 and 3) separated by the smallest digit of the previous term (1, present in ‘21’);

Why is a(7) equal to 13? Because 13 is the smallest unused integer that has two digits (1 and 3) separated by the smallest digit of the previous term (2, present in ‘23’);

Etc.

__________

The V sequence works on the same basis – just replace “smallest digit” in the definition by “biggest digit”:

> Underline the biggest digit of any a(n) in the sequence V. Now a(n+1) is the smallest integer not occurring earlier that has two digits separated by the underlined digit. Starting V with a(1)=1 should give:

V = 1, 10, 12, 13, 14, 15, 16, 17, 18, 19, 90, 109, 190, 209, 290, 309, 390, 409, 490, 509, 590, 609, 690, 709, 790, 809, 890, 900, 901, 902, 903, 904, 905, 906, 907, 908, 909, 910, 920, 930, 940, 950, 960, 970, 980, 990,...

Best,

É.

__________

[Hans Havermann]

I’ve put a couple of things in here:

bU.txt is an 18 MB b-file of 1250000 terms

bU.png is a plot of those points

U1.png,

U2.png,

U3.png are graphs of lesser numbers of (joined) points

V : from term #11 on, these are just the ordered numbers containing at least one nine and one zero.

__________

Many thanks, Hans – this is just beautiful! I reproduce (some of) your computations hereunder.

__________

The first 750 terms of U:

U = 1, 10, 11, 12, 21, 23, 13, 32, 20, 22, 24, 31, 34, 14, 43, 25, 35, 30, 33, 36, 41, 45, 15, 54, 26, 42, 46, 37, 47, 40, 44, 48, 51, 56, 16, 65, 27, 53, 52, 57, 38, 58, 49, 59, 50, 55, 61, 67, 17, 76, 28, 64, 62, 68, 39, 63, 69, 60, 66, 71, 78, 18, 87, 29, 75, 72, 79, 70, 77, 81, 89, 19, 98, 80, 88, 91, 100, 99, 90, 101, 110, 111, 102, 112, 103, 113, 104, 114, 105, 115, 106, 116, 107, 117, 108, 118, 109, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 134, 140, 133, 142, 143, 145, 150, 141, 152, 154, 156, 160, 144, 162, 165, 167, 170, 151, 172, 176, 178, 180, 155, 182, 187, 189, 190, 161, 192, 198, 201, 166, 203, 171, 210, 177, 211, 212, 213, 214, 215, 216, 217, 218, 219, 221, 223, 86, 82, 97, 92, 135, 230, 181, 231, 232, 136, 233, 137, 234, 138, 235, 139, 236, 146, 237, 153, 238, 157, 239, 163, 241, 243, 164, 245, 168, 251, 253, 173, 254, 175, 256, 179, 261, 263, 183, 265, 186, 267, 193, 271, 273, 197, 276, 200, 188, 278, 202, 191, 281, 283, 204, 199, 287, 205, 220, 222, 206, 224, 207, 225, 208, 226, 209, 227, 240, 228, 242, 244, 246, 247, 248, 249, 250, 229, 257, 260, 252, 264, 268, 270, 255, 274, 275, 279, 280, 262, 284, 286, 290, 266, 294, 297, 301, 272, 302, 277, 305, 282, 310, 288, 311, 289, 312, 291, 293, 313, 298, 314, 304, 292, 315, 320, 299, 316, 321, 322, 317, 323, 318, 324, 319, 325, 331, 326, 335, 74, 73, 85, 83, 96, 93, 147, 327, 341, 328, 342, 345, 148, 329, 346, 149, 332, 350, 300, 303, 330, 333, 158, 334, 169, 340, 336, 174, 343, 184, 344, 185, 347, 194, 348, 196, 349, 258, 351, 352, 353, 259, 354, 269, 355, 285, 356, 295, 357, 296, 358, 306, 337, 307, 338, 308, 339, 309, 363, 360, 366, 361, 362, 359, 364, 365, 367, 368, 369, 370, 373, 374, 376, 380, 377, 385, 386, 390, 383, 396, 401, 388, 403, 393, 407, 399, 410, 400, 404, 411, 372, 371, 378, 412, 382, 375, 413, 384, 414, 387, 415, 389, 416, 392, 379, 417, 394, 418, 398, 419, 405, 422, 381, 421, 423, 391, 425, 395, 427, 397, 430, 424, 402, 433, 431, 432, 406, 434, 436, 437, 441, 435, 447, 84, 95, 94, 159, 438, 451, 439, 452, 420, 440, 442, 426, 428, 429, 446, 195, 443, 457, 408, 444, 409, 445, 448, 450, 449, 458, 459, 460, 454, 462, 453, 461, 455, 468, 470, 464, 473, 463, 467, 478, 480, 466, 481, 456, 482, 465, 483, 469, 484, 485, 486, 487, 488, 489, 490, 474, 495, 498, 501, 477, 504, 494, 509, 499, 510, 500, 505, 511, 475, 512, 476, 513, 493, 471, 506, 515, 514, 516, 521, 523, 472, 479, 517, 524, 492, 496, 518, 526, 497, 519, 532, 502, 522, 503, 525, 507, 533, 491, 534, 508, 535, 520, 544, 529, 527, 530, 545, 531, 536, 528, 537, 538, 541, 540, 550, 551, 542, 539, 547, 548, 549, 559, 560, 552, 543, 558, 561, 546, 562, 553, 563, 568, 570, 554, 569, 572, 557, 580, 555, 583, 574, 571, 556, 590, 565, 594, 573, 578, 601, 566, 605, 575, 610, 577, 611, 564, 579, 612, 567, 613, 576, 614, 584, 581, 586, 615, 587, 616, 589, 617, 596, 618, 598, 619, 607, 585, 621, 623, 593, 582, 597, 627, 602, 588, 631, 625, 604, 595, 638, 592, 608, 599, 641, 632, 620, 600, 606, 622, 624, 628, 634, 603, 626, 635, 609, 633, 629, 640, 636, 630, 644, 591, 637, 639, 643, 647, 642, 645, 648, 651, 650, 646, 652, 649, 659, 661, 653, 658, 671, 654, 662, 657, 672, 664, 673, 663, 669, 660, 655, 681, 656, 683, 674, 682, 668, 670, 665, 691, 667, 680, 666, 690, 676, 693, 679, 701, 677, 706, 686, 710, 688, 711, 675, 694, 684, 692, 678, 712, 685, 702, 696, 713, 687, 714, 689, 715, 695, 705, 699, 716, 697, 717, 698, 718, 708, 700, 707, 722, 709, 727, 719, 721, 723, 720, 733, 703, 737, 704, 744, 726, 724, 725, 729, 731, 728, 735, 730, 747, 732, 739, 734, 736, 740, 755, 738, 741, 743, 742, 745, 748, 751, 746, 753, 749, 759, 750, 757, 752, 754, 762,...

U, graph of the first 750 (joined) points:

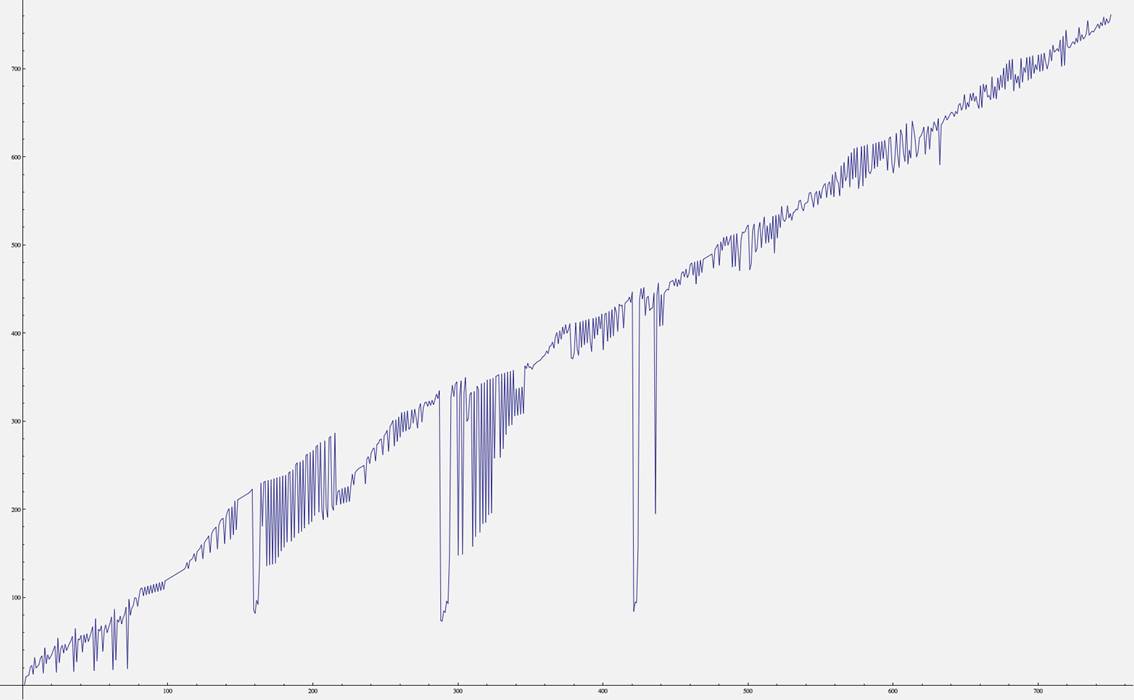
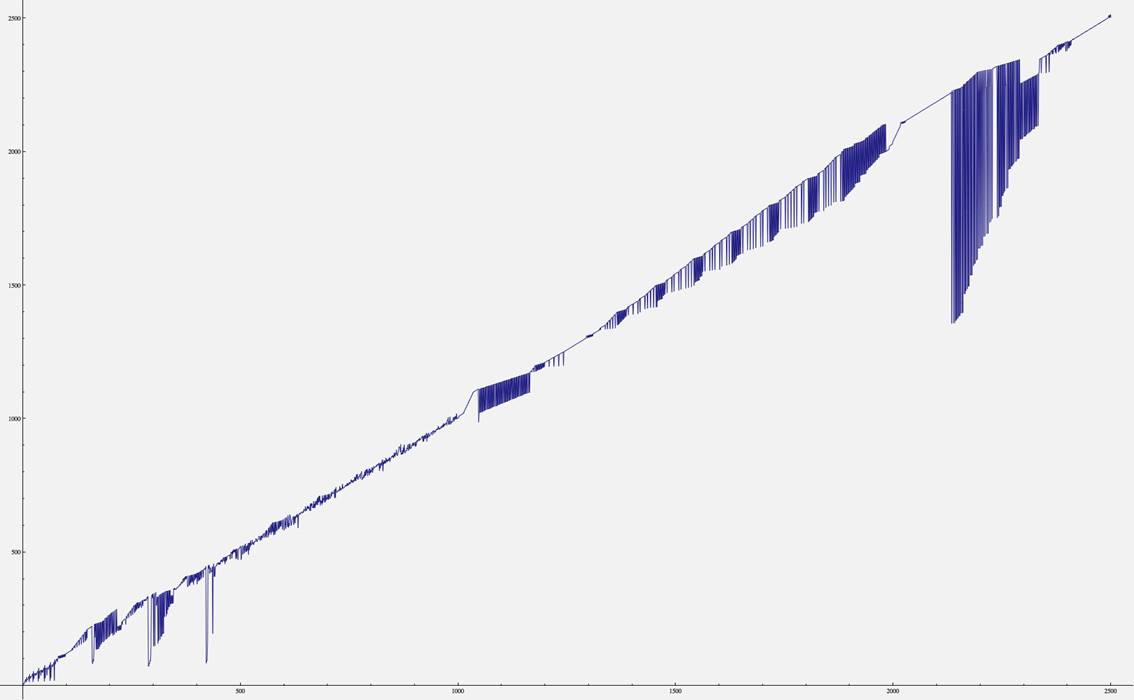
U, graph of the first 2500 (joined) points:

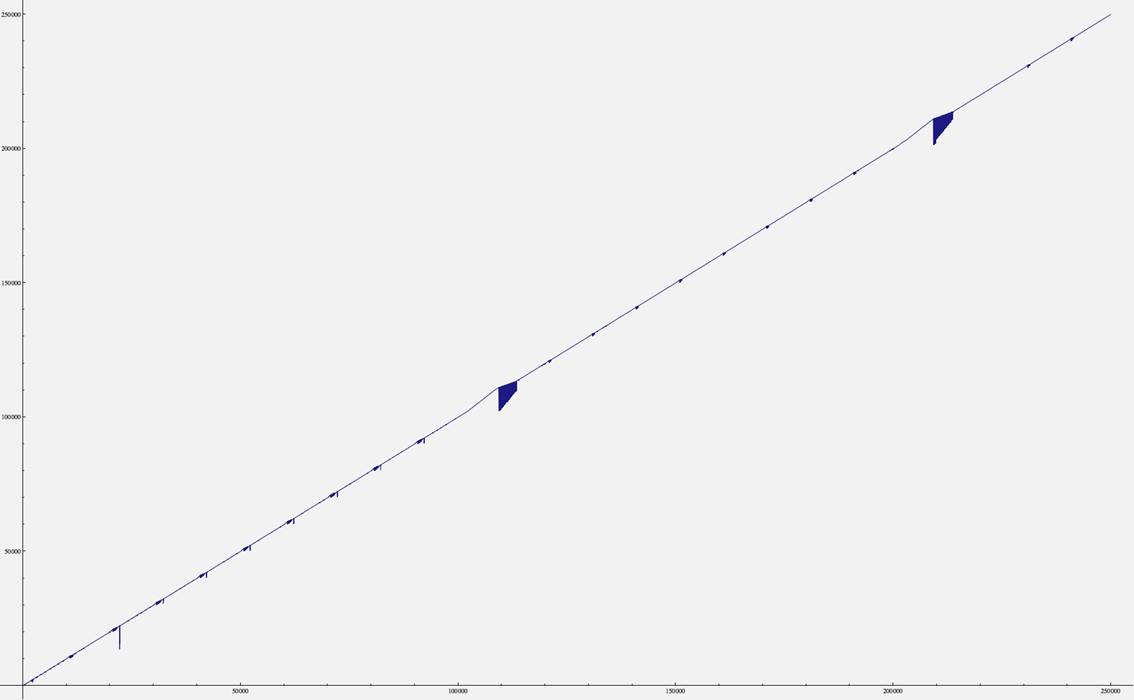
U, graph of the first 250 000 (joined) points:

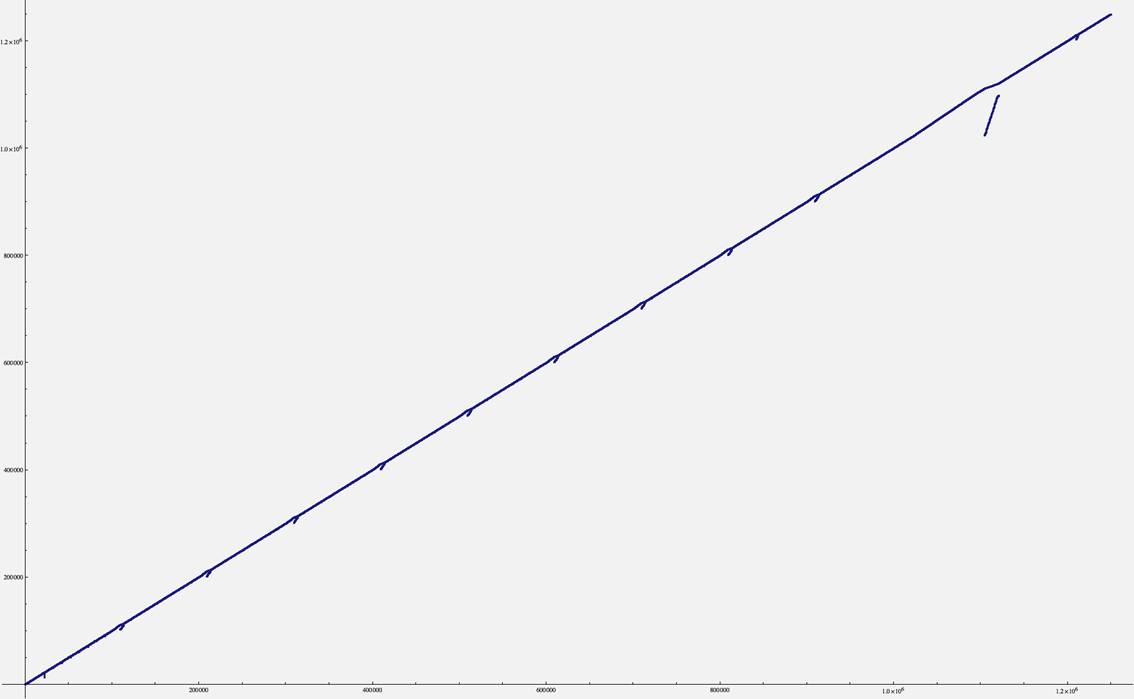
U, graph of the first 1.25 million terms:

__________

Me:

> Doesn’t the “isolated” short blue line on the top right suggest that U is kind of fractal?

Hans:

> Yes, there is a fractal aspect to this sequence. This will be A235828.

Again, many thanks to Hans!

Best,

É.