Waterfalls
(of
multiplications)
Hello SeqFans,
Start S with a(1) > 9
Now a(n) is simply the result of a
multiplication : [the (n-1)th digit of S] x [the n-th digit of S]
Let’s start S respectively with a(1) = [10, 11,
12, 13, 14, 15, 16, ...]
S = 10,0,0,0,0,0,0,0,...
S = 11,1,1,1,1,1,1,1,...
__
S =
12,2,4,8,32,24,6,4,8,24,24,32,16,8,8,8,12,6,2,6,48,64,64,8,2,12,12,12,24,32,...
__
S =
13,3,9,27,18,14,7,8,8,4,28,56,64,32,8,16,40,30,36,24,12,6,16,8,6,24,0,0,0,0,18,...
__
S = 14,4,16,4,6,24,12,8,4,2,16,32,8,2,6,18,6,16,16,12,6,8,48,6,6,6,6,6,2,12,48,32,32,...
S = 15,5,25,10,10,5,0,0,0,0,0,0,0,0,...
__
S = 16,6,36,18,18,6,8,8,8,48,48,64,64,32,...
__
(the "overlined"
multiplications --like 48-- produce the last computed so far term of some of
the above sequences)
Question:
What are the integers >9 which end on a fixed point (a fixed point
like 0 or 1) or end in a loop?
Respectively, what are the integers escaping fixed points and loops?
Though a 2-digit multiplication cannot produce a term > 81, I’ve
noticed that 13, for instance, never ends in a loop -- because the first
"0,0,0,0" pattern will turn later in a
"0,0,0,0,0" (5-zeroes) pattern, which will turn later in a 6-zeroes
pattern, than 7-zeroes, etc. -- and between those 0-patterns you will always
count more and more digits...
Best,
É.
__________
Hans Havermann
was quick to compute and draw this:
> For each n = 10, 11, ... 200, first a graph of 2000 terms of S, followed
immediately by a graph of 2000 digits of S:
> http://chesswanks.com/num/waterfalls/
Maximilian Hasler has sent me this comment (in French) and the S-sequences for n= 12 to 20 (illustrated below with the diagrams
provided by Hans Havermann’s link):
(...) il est probable que tout nombre finit par entrer dans un cycle "quasi-périodique" qui peut être complètement décrit (du genre: f(n) fois ça, g(n) fois ça, h(n) fois ça... et on recommence avec n+1 (...)
[Programme]:
casc = (a,n=200)->my(S=eval(Vec(Str(a))));for(i=1,n,i>1&S=concat(vecextract(S,"^1"),eval(Vec(Str(a=S[1]*S[2]))));print1(a","))
gp > casc(12,400)
12, 2, 4, 8, 32, 24, 6, 4, 8, 24, 24, 32, 16, 8, 8, 8, 12, 6, 2, 6, 48, 64, 64, 8, 2, 12, 12, 12, 24, 32, 48, 24, 24, 24, 32, 16, 2, 2, 2, 2, 2, 2, 4, 8, 12, 6, 8, 32, 16, 8, 8, 8, 8, 8, 12, 6, 2, 6, 12, 4, 4, 4, 4, 4, 8, 32, 8, 2, 12, 48, 24, 6, 2, 6, 48, 64, 64, 64, 64, 8, 2, 12, 12, 12, 6, 2, 8, 16, 16, 16, 16, 32, 24, 6, 16, 16, 2, 2, 8, 32, 16, 8, 24, 12, 12, 24, 32, 48, 24, 24, 24, 24, 24, 24, 24, 32, 16, 2, 2, 2, 2, 2, 2, 12, 12, 16, 8, 6, 6, 6, 6, 6, 6, 6, 18, 6, 4, 8, 24, 6, 6, 6, 6, 12, 4, 16, 24, 6, 2, 6, 48, 16, 8, 4, 2, 2, 2, 4, 8, 12, 6, 8, 32, 16, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 12, 6, 2, 6, 12, 4, 4, 4, 4, 4, 2, 2, 2, 2, 2, 6, 48, 48, 36, 36, 36, 36, 36, 36, 6, 8, 48, 24, 32, 16, 8, 24, 36, 36, 36, 6, 2, 8, 4, 6, 12, 8, 24, 12, 12, 24, 32, 8, 6, 48, 32, 8, 4, 4, 8, 32, 8, 2, 12, 48, 24, 6, 2, 6, 48, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 8, 2, 12, 12, 12, 6, 2, 8, 16, 16, 16, 16, 8, 4, 4, 4, 4, 12, 24, 32, 32, 32, 24, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 36, 48, 32, 32, 16, 8, 12, 6, 2, 6, 48, 16, 8, 12, 18, 18, 18, 18, 18, 36, 12, 16, 32, 24, 6, 2, 16, 16, 8, 4, 2, 2, 2, 4, 8, 12, 6, 16, 48, 24, 32, 24, 6, 16, 32, 16, 32, 24, 6, 16, 16, 2, 2, 8, 32, 16, 8, 24, 12, 12, 24, 32, 48, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 32, 16, 2, 2, 2, 2, 2, 2, 12, 12, 16, 8, 6, 6, 6, 6, 6, 6, 6, 48, 32, 16, 16, 16, 4, 2, ...
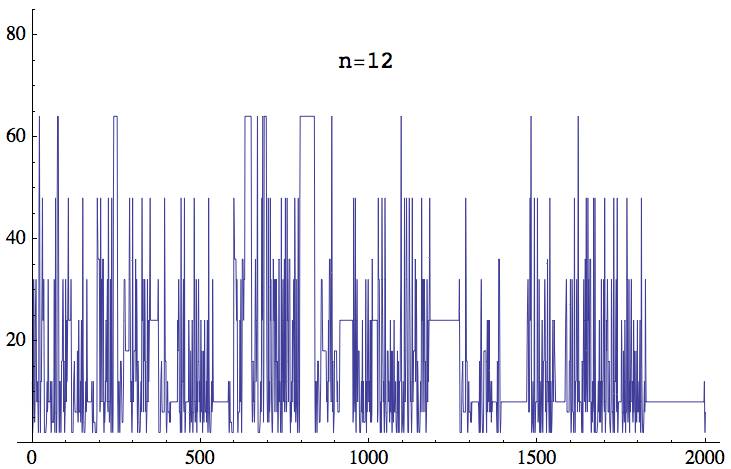
gp > casc(13,400)
13, 3, 9, 27, 18, 14, 7, 8, 8, 4, 28, 56, 64, 32, 8, 16, 40, 30, 36, 24, 12, 6, 16, 8, 6, 24, 0, 0, 0, 0, 18, 12, 8, 4, 2, 12, 6, 6, 48, 48, 12, 8, 0, 0, 0, 0, 0, 8, 8, 2, 16, 32, 8, 2, 2, 12, 36, 24, 32, 32, 32, 8, 2, 16, 0, 0, 0, 0, 0, 0, 64, 16, 2, 6, 18, 6, 16, 16, 4, 2, 2, 6, 18, 12, 8, 12, 6, 6, 6, 6, 6, 16, 16, 2, 6, 0, 0, 0, 0, 0, 0, 0, 24, 4, 6, 12, 12, 6, 8, 48, 6, 6, 6, 6, 24, 8, 4, 12, 6, 8, 8, 2, 16, 8, 2, 12, 36, 36, 36, 36, 6, 6, 6, 6, 12, 12, 0, 0, 0, 0, 0, 0, 0, 0, 8, 16, 24, 6, 2, 2, 2, 12, 48, 32, 32, 48, 36, 36, 36, 12, 8, 32, 32, 4, 2, 12, 48, 64, 16, 2, 6, 48, 16, 2, 2, 6, 18, 18, 18, 18, 18, 18, 18, 36, 36, 36, 36, 6, 2, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 8, 6, 12, 8, 24, 12, 4, 4, 2, 2, 8, 32, 24, 6, 6, 6, 8, 32, 24, 18, 18, 18, 18, 18, 6, 2, 16, 24, 6, 6, 6, 8, 8, 2, 2, 8, 32, 48, 24, 4, 6, 12, 12, 24, 32, 8, 6, 12, 4, 12, 6, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 24, 18, 18, 18, 18, 18, 18, 18, 36, 12, 4, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 48, 6, 2, 16, 16, 8, 4, 2, 8, 16, 8, 4, 16, 24, 6, 4, 8, 24, 36, 36, 48, 24, 6, 4, 8, 4, 8, 8, 8, 8, 8, 8, 8, 8, 8, 48, 12, 2, 6, 12, 8, 24, 36, 36, 48, 64, 16, 4, 16, 24, 6, 8, 32, 16, 8, 16, 24, 6, 2, 2, 2, 4, 8, 12, 6, 16, 48, 6, 2, 8, 4, 2, 12, 48, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 16, 8, 4, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 24, 18, 6, 2, 8, 16, 0, 0, 0, 0, 0, 0, ...
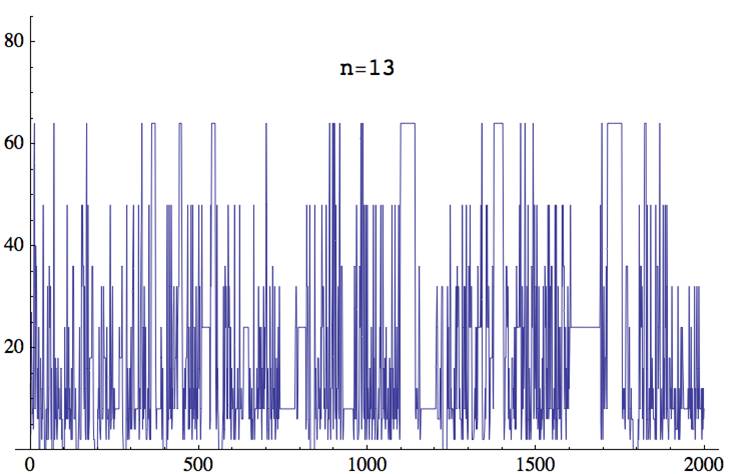
gp > casc(14,400)
14, 4, 16, 4, 6, 24, 24, 12, 8, 8, 8, 4, 2, 16, 64, 64, 32, 8, 2, 6, 36, 24, 24, 24, 12, 6, 16, 16, 12, 18, 18, 12, 8, 8, 8, 8, 8, 4, 2, 12, 6, 6, 6, 6, 6, 2, 2, 8, 8, 8, 8, 2, 16, 64, 64, 64, 64, 32, 8, 2, 2, 12, 36, 36, 36, 36, 12, 4, 16, 64, 64, 64, 16, 2, 6, 36, 24, 24, 24, 24, 24, 24, 24, 12, 6, 16, 16, 4, 2, 2, 6, 18, 18, 18, 18, 18, 18, 18, 6, 2, 8, 4, 6, 36, 24, 24, 24, 24, 24, 4, 6, 12, 12, 18, 18, 12, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 4, 2, 12, 6, 6, 6, 6, 24, 8, 4, 12, 6, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 48, 12, 16, 32, 24, 18, 18, 12, 8, 8, 8, 8, 8, 8, 8, 8, 8, 16, 24, 6, 2, 2, 2, 2, 8, 8, 8, 8, 2, 16, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 32, 8, 2, 2, 12, 36, 36, 36, 12, 8, 32, 32, 4, 2, 12, 48, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 32, 32, 8, 2, 2, 6, 18, 6, 4, 8, 4, 8, 8, 8, 8, 2, 16, 64, 64, 64, 64, 64, 64, 64, 64, 8, 6, 12, 8, 24, 12, 4, 4, 4, 16, 64, 64, 64, 16, 2, 6, 36, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 12, 6, 16, 16, 4, 2, 2, 6, 18, 18, 18, 18, 18, 6, 2, 16, 24, 6, 6, 6, 8, 8, 2, 2, 8, 32, 48, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 12, 6, 6, 6, 16, 16, 4, 12, 6, 8, 48, 24, 32, 32, 32, 64, 64, 64, 16, 2, 6, 36, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 32, 48, 6, 2, 16, 16, 8, 4, 2, 8, 16, 16, 4, 6, 36, 24, 24, 24, 24, 24, 4, 6, 12, 12, ...
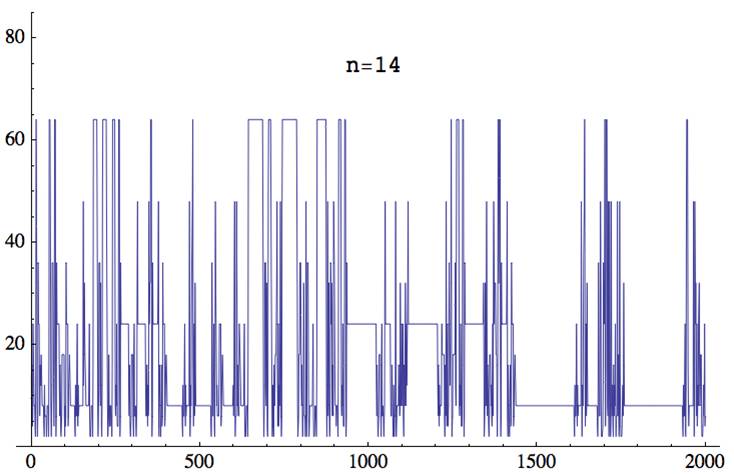
gp > casc(15,400)
15,5,25,10,10,5,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, ...
(03:41) gp > casc(16,400)
16, 6, 36, 18, 18, 6, 8, 8, 8, 48, 48, 64, 64, 32, 32, 32, 32, 48, 24, 24, 24, 12, 6, 6, 6, 6, 6, 6, 6, 8, 32, 16, 8, 8, 8, 8, 8, 4, 2, 12, 36, 36, 36, 36, 36, 36, 48, 24, 6, 2, 6, 48, 64, 64, 64, 64, 32, 8, 2, 2, 6, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 24, 32, 16, 8, 24, 12, 12, 24, 32, 48, 24, 24, 24, 24, 24, 24, 24, 12, 6, 16, 16, 4, 12, 6, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 16, 8, 12, 6, 2, 6, 48, 16, 8, 4, 2, 2, 2, 4, 8, 12, 6, 8, 32, 16, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 4, 2, 12, 6, 6, 6, 6, 24, 4, 2, 12, 48, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 8, 6, 48, 8, 2, 12, 12, 12, 24, 32, 8, 6, 48, 32, 8, 4, 4, 8, 32, 8, 2, 12, 48, 24, 6, 2, 6, 48, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 32, 8, 2, 2, 12, 36, 36, 36, 12, 8, 16, 8, 2, 2, 8, 32, 48, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 32, 48, 24, 32, 64, 16, 2, 2, 2, 2, 2, 2, 4, 8, 12, 6, 16, 48, 24, 32, 24, 6, 16, 32, 16, 32, 24, 6, 16, 16, 2, 2, 8, 32, 16, 8, 24, 12, 12, 24, 32, 48, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 12, 6, 16, 16, 4, 2, 2, 6, 18, 18, 18, 18, 18, 6, 2, 16, 8, 6, 48, 16, 4, 16, 24, 6, 8, 32, 16, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, ...
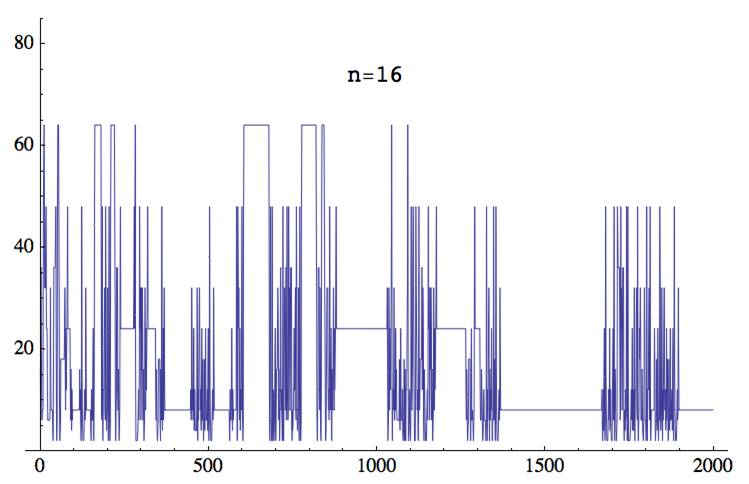
gp > casc(17,400)
17, 7, 49, 28, 36, 18, 16, 24, 18, 6, 8, 8, 6, 12, 8, 4, 8, 48, 48, 64, 48, 6, 2, 16, 32, 32, 32, 32, 32, 32, 48, 24, 16, 32, 48, 12, 2, 6, 18, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 8, 32, 16, 8, 4, 6, 18, 6, 8, 32, 8, 2, 4, 12, 6, 8, 48, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, 48, 24, 6, 2, 6, 48, 32, 24, 6, 8, 48, 48, 24, 6, 16, 16, 8, 4, 2, 12, 48, 32, 32, 24, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 24, 32, 16, 8, 24, 12, 12, 24, 32, 24, 6, 4, 8, 24, 48, 32, 32, 32, 32, 16, 8, 24, 6, 6, 6, 6, 48, 32, 8, 2, 2, 8, 32, 24, 6, 6, 6, 4, 8, 4, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 16, 8, 12, 6, 2, 6, 48, 16, 8, 4, 2, 2, 2, 4, 8, 12, 6, 4, 8, 24, 24, 32, 16, 8, 16, 32, 24, 6, 6, 6, 6, 6, 6, 6, 2, 6, 48, 16, 8, 24, 36, 36, 36, 24, 32, 24, 6, 16, 16, 4, 16, 24, 6, 4, 8, 24, 36, 36, 24, 32, 32, 32, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 8, 6, 48, 8, 2, 12, 12, 12, 24, 32, 8, 6, 48, 32, 8, 4, 4, 8, 32, 8, 2, 12, 24, 32, 16, 8, 8, 8, 12, 6, 2, 6, 48, 8, 6, 18, 6, 4, 8, 24, 36, 36, 36, 36, 36, 36, 12, 12, 24, 32, 8, 6, 48, 16, 8, 12, 18, 18, 18, 18, 18, 12, 8, 12, 6, 4, 8, 24, 6, 6, 6, 6, 24, 4, 6, 12, 8, 24, 24, 32, 16, 8, 12, 18, 18, 18, 12, 8, 12, 6, 6, 6, 6, 6, 12, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, ...
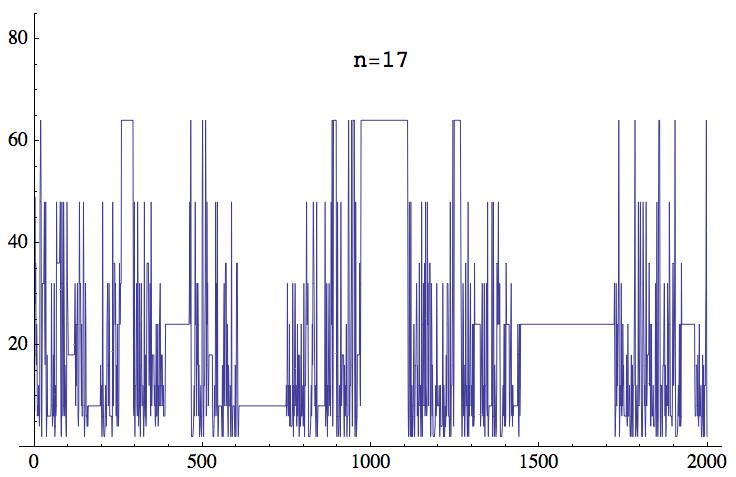
gp > casc(18,400)
18, 8, 64, 48, 24, 16, 32, 16, 8, 4, 6, 18, 6, 2, 6, 48, 32, 24, 6, 8, 48, 12, 12, 24, 32, 24, 6, 4, 8, 24, 48, 32, 32, 8, 2, 2, 2, 4, 8, 12, 6, 4, 8, 24, 24, 32, 16, 8, 16, 32, 24, 6, 6, 6, 16, 16, 4, 4, 8, 32, 8, 2, 12, 24, 32, 16, 8, 8, 8, 12, 6, 2, 6, 48, 8, 6, 18, 6, 4, 8, 24, 36, 36, 6, 6, 6, 6, 24, 16, 32, 24, 6, 16, 16, 2, 2, 4, 8, 12, 6, 2, 6, 48, 64, 64, 8, 2, 12, 12, 12, 24, 32, 64, 48, 6, 8, 48, 24, 32, 16, 8, 12, 18, 18, 18, 36, 36, 36, 36, 12, 8, 4, 6, 18, 6, 4, 8, 24, 6, 6, 6, 6, 12, 4, 8, 32, 8, 2, 12, 12, 12, 24, 32, 48, 24, 24, 24, 32, 16, 2, 2, 2, 2, 2, 2, 4, 8, 12, 6, 12, 24, 16, 32, 48, 48, 32, 32, 16, 8, 12, 6, 2, 6, 48, 8, 2, 2, 8, 8, 8, 8, 8, 24, 18, 18, 18, 18, 18, 18, 18, 6, 2, 16, 32, 24, 6, 8, 48, 24, 32, 16, 8, 24, 36, 36, 36, 6, 2, 8, 32, 24, 6, 16, 16, 2, 2, 2, 2, 2, 2, 4, 8, 12, 6, 8, 32, 16, 8, 8, 8, 8, 8, 12, 6, 2, 6, 12, 4, 4, 4, 4, 4, 8, 32, 8, 2, 12, 6, 2, 4, 8, 4, 6, 18, 6, 8, 32, 32, 32, 24, 6, 6, 6, 2, 6, 48, 8, 2, 12, 12, 12, 24, 32, 64, 16, 4, 16, 64, 64, 64, 64, 16, 8, 4, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 48, 12, 2, 6, 18, 6, 4, 8, 24, 48, 32, 32, 16, 8, 12, 6, 2, 6, 48, 16, 8, 12, 18, 18, 18, 18, 18, 36, 12, 16, 24, 6, 4, 8, 24, 6, 6, 6, 6, 12, 4, 4, 4, 4, 4, 8, 32, 8, 2, 12, 48, 24, 6, 2, 6, 48, 64, 64, 64, 64, 8, 2, 12, 12, 12, 6, 2, 8, 16, 16, 16, 16, 32, 24, 6, 16, 16, 2, 2, 12, 12, 8, 32, 32, 24, 6, 8, 48, 48, 24, 6, 6, 6, ...
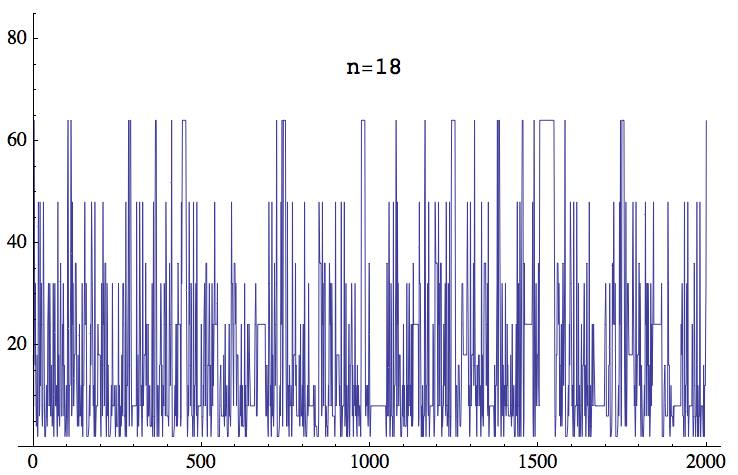
gp > casc(19,400)
19, 9, 81, 72, 8, 7, 14, 16, 56, 7, 4, 4, 6, 30, 30, 42, 28, 16, 24, 18, 0, 0, 0, 0, 8, 4, 16, 8, 6, 12, 8, 4, 8, 0, 0, 0, 0, 0, 32, 4, 6, 48, 48, 6, 2, 16, 32, 32, 0, 0, 0, 0, 0, 0, 6, 8, 24, 24, 32, 32, 32, 48, 12, 2, 6, 18, 6, 6, 6, 0, 0, 0, 0, 0, 0, 0, 48, 16, 8, 8, 8, 12, 6, 6, 6, 6, 6, 8, 32, 8, 2, 4, 12, 6, 8, 48, 36, 36, 0, 0, 0, 0, 0, 0, 0, 0, 32, 8, 6, 48, 64, 64, 8, 2, 12, 36, 36, 36, 36, 48, 24, 6, 16, 16, 8, 4, 2, 12, 48, 32, 32, 24, 18, 18, 18, 0, 0, 0, 0, 0, 0, 0, 0, 0, 6, 16, 48, 24, 32, 48, 24, 24, 24, 32, 16, 2, 2, 6, 18, 18, 18, 18, 18, 18, 18, 24, 32, 16, 8, 24, 6, 6, 6, 6, 48, 32, 8, 2, 2, 8, 32, 24, 6, 6, 6, 4, 8, 4, 8, 8, 8, 8, 8, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 6, 6, 24, 32, 16, 8, 12, 6, 8, 32, 16, 8, 8, 8, 8, 8, 12, 6, 2, 6, 12, 4, 12, 6, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 16, 8, 12, 6, 2, 6, 48, 16, 8, 24, 36, 36, 36, 24, 32, 24, 6, 16, 16, 4, 16, 24, 6, 4, 8, 24, 36, 36, 24, 32, 32, 32, 64, 64, 64, 64, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 36, 12, 8, 12, 6, 2, 6, 48, 8, 2, 12, 48, 24, 6, 2, 6, 48, 64, 64, 64, 64, 8, 2, 12, 12, 12, 6, 2, 8, 4, 2, 12, 48, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 8, 6, 48, 8, 2, 12, 12, 12, 24, 32, 8, 6, 48, 16, 8, 12, 18, 18, 18, 18, 18, 12, 8, 12, 6, 4, 8, 24, 6, 6, 6, 6, 24, 4, 6, 12, 8, 24, 24, 32, 16, 8, 12, 18, 18, 18, 12, 8, 12, 6, 6, 6, 6, 6, 12, 24, 24, 24, 24, 24, 24, 24, 0, 0, 0, 0, 0, 0, ...
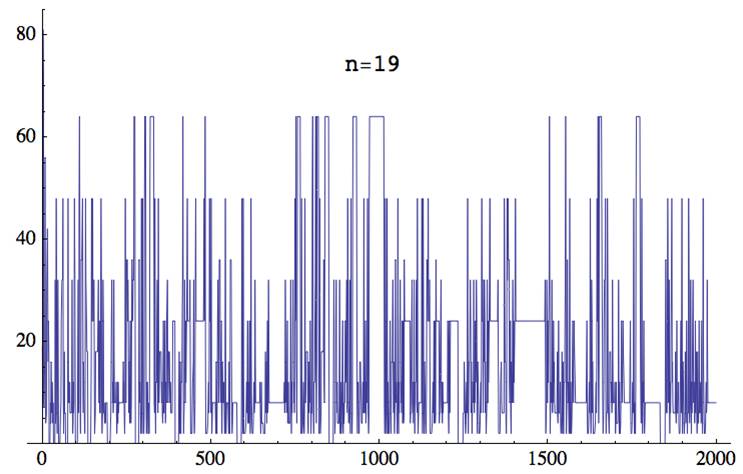
Thanks to everyone,
Best,
É.
__________
Update, March 27th, 2012 (in French)
Maximilian Hasler:
Liste des nombres <1000 qui terminent en [0,0,0,0,0,0...] (liste calculée en approche expérimentale, n’est donc pas 100% rigoureuse, mais semble juste) :
10, 15, 20, 25, 30, 35, 40, 45, 50, 51, 52, 53, 54, 55, 56, 57, 58, 60, 65, 69, 70, 75, 78, 80, 85, 87, 90, 95, 96, 98, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 115, 120, 125, 130, 135, 140, 145, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 165, 169, 170, 175, 178, 180, 185, 187, 190, 196, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 215, 220, 225, 230, 235, 240, 245, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 265, 270, 275, 280, 285, 290, 300, 301, 302, 303, 304, 305, 306, 307, 308, 309, 310, 315, 320, 325, 330, 335, 340, 345, 350, 351, 352, 353, 354, 355, 356, 357, 358, 359, 360, 365, 370, 375, 380, 385, 390, 400, 401, 402, 403, 404, 405, 406, 407, 408, 409, 410, 415, 420, 425, 430, 435, 440, 445, 450, 451, 452, 453, 454, 455, 456, 457, 458, 459, 460, 465, 470, 480, 485, 490, 500, 501, 502, 503, 504, 505, 506, 507, 508, 509, 510, 511, 512, 513, 514, 515, 516, 517, 518, 520, 521, 522, 523, 524, 525, 526, 527, 528, 529, 530, 531, 532, 535, 540, 541, 542, 543, 544, 545, 546, 548, 550, 551, 552, 553, 554, 555, 556, 557, 558, 559, 560, 561, 562, 563, 564, 565, 567, 569, 570, 575, 580, 581, 582, 583, 584, 585, 587, 590, 595, 600, 601, 602, 603, 604, 605, 606, 607, 608, 609, 610, 615, 619, 620, 625, 630, 635, 640, 645, 650, 651, 652, 653, 654, 655, 656, 657, 658, 659, 660, 670, 680, 690, 695, 696, 700, 701, 702, 703, 704, 705, 706, 707, 708, 709, 710, 715, 718, 720, 725, 730, 735, 740, 750, 751, 752, 753, 754, 755, 756, 757, 758, 760, 765, 770, 780, 785, 787, 790, 800, 801, 802, 803, 804, 805, 806, 807, 808, 809, 810, 815, 817, 820, 825, 830, 835, 840, 845, 850, 851, 852, 853, 854, 855, 856, 857, 858, 859, 860, 865, 870, 872, 873, 875, 878, 880, 885, 890, 900, 901, 902, 903, 904, 905, 906, 907, 908, 909, 910, 915, 916, 920, 925, 930, 940, 950, 951, 952, 953, 954, 955, 956, 958, 960, 961, 962, 965, 969, 970, 980, 985, 990, 995, ...
Liste des nombres <10^4 ne comportant ni chiffre 0, ni 5 mais qui finissent en [0,0,0,0,0,0,0, ...] :
69, 78, 87, 96, 98, 169, 178, 187, 196, 619, 696, 718, 787, 817, 872, 873, 878, 916, 961, 962, 969, 1169, 1178, 1691, 1781, 2987, 6911, 6916, 6961, 6962, 6969, 7817, 7872, 7873, 7878, 8117, 9116, 9696, 9878, ...
Liste des nombres < 2000 (après ils sont trop nombreux) qui *ont* un chiffre 0 ou 5 mais ne finissent *pas* en [0,0,0,0,0,0, ...] :
59, 195, 295, 395, 475, 495, 519, 533, 534, 536, 537, 538, 539, 547,549, 566, 568, 572, 573, 574, 576, 577, 578, 579, 586, 588, 589, 591,592, 593, 594, 596, 597, 598, 599, 665, 675, 685, 745, 759, 775, 795,895, 935, 945, 957, 959, 975, 1175, 1195, 1245, 1275, 1285, 1295,1325, 1335, 1353, 1356, 1358, 1359, 1365, 1375, 1385, 1395, 1445,1457, 1459, 1465, 1475, 1485, 1495, 1519, 1529, 1539, 1547, 1549,1566, 1567, 1568, 1574, 1577, 1579, 1589, 1593, 1594, 1597, 1615,1635, 1645, 1653, 1654, 1656, 1657, 1658, 1660, 1665, 1675, 1685,1715, 1725, 1735, 1745, 1751, 1752, 1753, 1754, 1756, 1757, 1759,1760, 1765, 1770, 1775, 1790, 1795, 1825, 1835, 1845, 1852, 1854,1856, 1857, 1858, 1859, 1860, 1865, 1880, 1885, 1895, 1925, 1930,1935, 1940, 1945, 1950, 1951, 1952, 1953, 1954, 1955, 1956, 1957,1958, 1959, 1975, 1980, 1985, 1995,
Merci Maximilian!
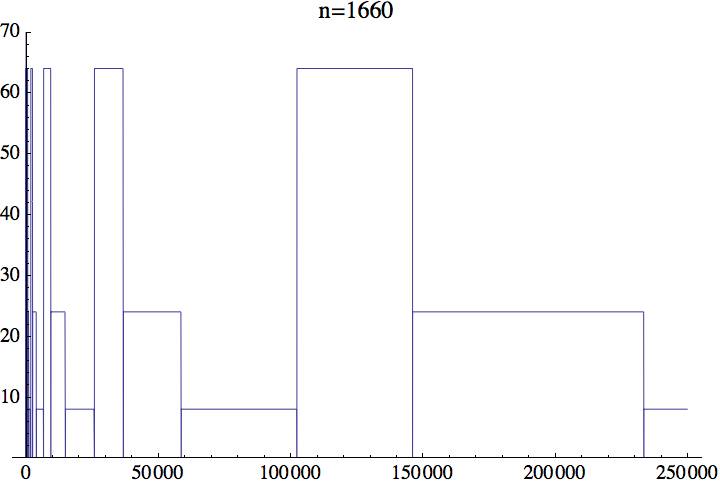
À propos du 1660 surligné ci-dessus,
Hans Havermann écrit
ceci:
I had a detailed look at 1660 because I had mis-guessed that a number containing a zero would end in all-zeros. While not a "loop", the evolution looked regular enough that I wondered if I could describe it. And I believe that I can: After the initial 1660,6,36,0,0,18,18, we get "expanding cycles", for n=1...infinity, of 3n zeros,
(4^n+8)/6+1 eights,
3n+1 zeros,
(4^n+8)/6 sixty-fours,
3n+2 zeros,
(4^n+8)/3-1 twenty-fours:
1660, 6, 36, 0, 0, 18, 18, 0, 0, 0, 8, 8, 8, 0, 0, 0, 0, 64, 64, 0, 0, 0, 0, 0, 24, 24, 24, 0, 0, 0, 0, 0, 0, 8, 8, 8, 8, 8, 0, 0, 0, 0, 0, 0, 0, 64, 64, 64, 64, 0, 0, 0, 0, 0, 0, 0, 0, 24, 24, 24, 24, 24, 24, 24, 0, 0, 0, 0, 0, 0, 0, 0, 0, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 0, ...
|
n |
zeros |
eights |
zeros |
sixty-fours |
zeros |
twenty-fours |
|
|
|
|
|
|
|
|
|
1 |
3 |
3 |
4 |
2 |
5 |
3 |
|
2 |
6 |
5 |
7 |
4 |
8 |
7 |
|
3 |
9 |
13 |
10 |
12 |
11 |
23 |
|
4 |
12 |
45 |
13 |
44 |
14 |
87 |
|
5 |
15 |
173 |
16 |
172 |
17 |
343 |
|
6 |
18 |
685 |
19 |
684 |
20 |
1367 |
|
7 |
21 |
2733 |
22 |
2732 |
23 |
5463 |
|
8 |
24 |
10925 |
25 |
10924 |
26 |
21847 |
|
9 |
27 |
43693 |
28 |
43692 |
29 |
87383 |
|
10 |
30 |
174765 |
31 |
174764 |
32 |
349527 |
|
11 |
33 |
699053 |
34 |
699052 |
35 |
1398103 |
|
12 |
36 |
2796205 |
37 |
2796204 |
38 |
5592407 |
|
13 |
39 |
11184813 |
40 |
11184812 |
41 |
22369623 |
|
14 |
42 |
44739245 |
43 |
44739244 |
44 |
89478487 |
|
15 |
45 |
178956973 |
46 |
178956972 |
47 |
357913943 |
|
16 |
48 |
715827885 |
49 |
715827884 |
50 |
1431655767 |
|
17 |
51 |
2863311533 |
52 |
2863311532 |
53 |
5726623063 |
|
18 |
54 |
11453246125 |
55 |
11453246124 |
56 |
22906492247 |
|
19 |
57 |
45812984493 |
58 |
45812984492 |
59 |
91625968983 |
|
20 |
60 |
183251937965 |
61 |
183251937964 |
62 |
366503875927 |
Here’s how it looks:
Maximilian Hasler avait exprimé la même idée de “périodicité paramétrée”:
(...) il est probable que tout nombre finit par entrer dans un cycle "quasi-périodique" qui peut être complètement décrit, du genre : f(n) fois ça, g(n) fois ça, h(n) fois ça... et on recommence avec (n+1).
Cette “quasi-périodicité”
avait inspiré à Gilles Esposito-Farèse
le commentaire suivant :
(...) Je crois qu’il s’agit d’orbites quasi-périodiques comme celles intermédiaires entre les tores périodiques et le chaos total, dans les systèmes hamiltoniens complexes, cf. http://goo.gl/SyXIz. On a généralement (i) des points fixes, (ii) des tores invariants autour de ces points fixes, (iii) des régions quasi-périodiques, (iv) un mélange complet des lignes d’univers.
Merci à tous,
à+
É.