A
seed and a jumping bean
Consider S:
S=0,1,1,1,2,3,1,3,6,3,1,5,10,7,1,3,14,7,1,13,18,7,1,3,22,11,1,21,26,15,1,3,30,7,1,29,34,15,1,3,38,27,1,37,42,15,1,3,46,7,
...
n=1,2,3,4,5,6,7,8,9,1,1,1, 1,1,1,1, 1,1,1, 2,
2,2,2,2, 2, 2,2, 2,
2, 3,3,3, 3,3,3, 3, 3, 3,3,4, 4, 4,4, 4, 4, 4,4,4, 4,5, ...
0 1 2
3 4 5 6 7 8 9 0 1 2
3 4 5 6 7 8
9 0 1 2 3 4 5
6 7 8 9 0
1 2 3 4
5 6 7 8 9
0
Read “n” vertically; thus S(10)=3,
S(25)=22 and S(47)=1, for instance.
S works like this:
- take any S(n), the “seed” [for instance if n=10, take S(10)=3 (this 3
is “the seed”)];
- jump
from S(n) to the right, over S(n) integers [from S(10)=3 over 1,5,10 (3
integers)];
- land on S[n+1+S(n)], “the bean” [land on 7, “the bean”];
S has been build in
order to always have S(n)+S[n+1+S(n)]=n [or
“seed”+“bean”=n thus 3+7=10].
This sequence is
infinite and well defined.
Here is how S was
build, step by step;
S = . . . . . . . . .
n = 1 2 3 4 5 6 7 8 9
If we put “1” at the
beginning of S, we will have a “0” in third position:
S = 1 . 0 . . . . . .
n = 1 2 3 4 5 6 7 8 9
This is because the
seed “1” asks us to jump over one integer (to the right) and land on the bean –
with “bean” + “seed” = 1.
If “0” can be an
integer of S, we’d better try to start S with “0” and see if the result works –
because we always prefer our S’s to be the lexicographic first ones.
We thus begin S with
“0”:
S = 0 . . . . . . . .
n = 1 2 3 4 5 6 7 8 9
This “0” asks us to jump over 0 integer and land on a “bean” such
that “bean” + “seed” = 1; we have then:
S = 0 1 . . . . . . .
n = 1 2 3 4 5 6 7 8 9
This “1” is now the
seed for another bean (such that “bean” + “seed” = n):
S = 0 1 . 1 . . . . .
n = 1 2 3 4 5 6 7 8 9
And this “1” is the
seed for a new bean (which has to obey the same “bean+seed=n”
law):
S = 0 1 . 1 . 3 . . .
n = 1 2 3 4 5 6 7 8 9
This “3” is itself a
new seed:
S = 0 1 . 1 . 3 . . . 3
n = 1 2 3 4 5 6 7 8 9
10
And this “3” is itself, etc.
S = 0 1 . 1 . 3 . . . 3 .
. . 7
n = 1 2 3 4 5 6 7 8 9
10 11 12 13 14
The “7” asks us to jump over 7 integers and to write “7” on the
landing space:
S = 0 1 . 1 . 3 . . . 3 .
. . 7 .
. . .
. . . 7 . .
. . .
. . .
n = 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
And this “7” forces a
“15” ( which comes from 22-7) above n = 30:
S = 0 1 . 1 . 3 . . . 3 .
. . 7 .
. . .
. . . 7 . .
. . .
. . 15
n = 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Etc.
This goes to
infinity, of course – but what about the “holes” we have left behind in S?
As we want S to be
the lexicographic first sequence with the property “seed+bean=n”,
we try to fill the leftmost hole --S(3)-- with a zero:
S = 0 1 0 1 . 3 . . . 3 . .
. 7 .
. . .
. . . 7 . .
. . .
. . 15
n = 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
But this doesn’t
work, as 0 + 1 (the “1” to the right of 0) is not 3 (the number under 0) as it
should be.
We then try to fill
the hole with “1”:
S = 0 1 1 1 . 3 . . . 3 . .
. 7 .
. . .
. . . 7 . .
. . .
. . 15
n = 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
... and this produces a “2” (in yellow) in the next hole –
because of the law “bean+seed=n”:
S = 0 1 1 1 2 3 . . . 3 . .
. 7 .
. . .
. . . 7 . .
. . .
. . 15
n = 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
But this “2” starts a
brand new infinite series of integers to the right, of course (new integer in
yellow):
S = 0 1 1 1 2 3 .
3
. 3 .
. . 7 .
. . .
. . . 7 . .
. . .
. . 15
n = 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
... then:
S = 0 1 1 1 2 3 .
3 . 3 . 5 . 7 .
. . .
. . . 7 . .
. . .
. . 15
n = 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
... and:
S = 0 1 1 1 2 3 .
3 . 3 . 5 .
7 . .
. 7 .
. . 7 .
. . .
. . . 15
n = 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
... further:
S = 0 1 1 1 2 3 .
3 . 3 . 5 .
7 . .
. 7 .
. . 7 .
. . 11 .
. . 15
n = 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
... etc.
We have a doubt,
here: will the two series “collide” at some point?
More: we notice immediately
that we’ll have to start another series of “seeds and beans”, because we have a
new leftmost hole to fill! Let’s start with that one – which is in position S(7) – and try to fill it with a “1” (as the “0” is
obviously leading to a contradiction):
S = 0 1 1 1 2 3 1 3 . 3 .
5 . 7 .
. . 7 .
. . 7 .
. . 11 .
. . 15
n = 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
... producing (in yellow):
S = 0 1 1 1 2 3 1 3 6 3
. 5 .
7 . .
. 7 .
. . 7 .
. . 11 .
. . 15
n = 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
... and:
S = 0 1 1 1 2 3 1 3 6 3
. 5 .
7 . 3 . 7 .
. . 7 .
. . 11 .
. . 15
n = 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
... further:
S = 0 1 1 1 2 3 1 3 6 3
. 5 .
7 . 3 .
7 . 13 .
7 . . . 11 . . . 15
n = 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Etc.
At my great surprise,
I’ve noticed that no “collisions” will ever occur if we always fill the
leftmost hole with a “1”!
I’ve tried yesterday
to understand the patterns arising in S. All I could find was this:
(a) S(4n-1)=1
(b) S(8n)=3
(c) S(8n+1)= 6+8(n-1)
(d) S(8n+4)= 5+8(n-1)
(e) S(8n+5)=10+8(n-1)
(f) S(16n+2)=7
I’m stuck in defining
S(4n+2) which would complete the description of all
terms of S after S(6)...
I hope I’ve made no
mistakes – and that this might be of interest for the Seqfans!
Best,
É.
__________
Jean-Paul Davalan:
(...)
En partant à la fois de S(n)+S[n+1+S(n)]=n et de S(4n-1)=1 (le premier
"pattern") et en opérant comme tu l’as fait avec le début de la
suite, on obtient TOUT le reste.
S(n)+S[n+1+S(n)]=n
peut se décliner sous la forme : S(n) = A <=> S(n+1+A) = n -
A
S(4n-1)
= 1 entraîne S(4n-1+1+1)=4n-1--1 c’est-à-dire
S(4n+1)
= 4n-2 (correspond aux 3e et 5e patterns)
et on recommence S(4n+1+4n-2+1)
= 4n+1-(4n-2) c’est-à-dire
S(8n)
= 3 le second "pattern"
S(8n+4)
= 8n -3 soit la 4e formule, puis S(8n+4 + 8n-3 + 1) = 8n+4
-(8n -3 )
S(16n+2)
= 7 soit la formule (f)
S(16n+10)
= 16n -5 qui correspond à S(4(4p+2)+2) = 4(4p+2)-3, c’est-à-dire à
S(4n+2) = 4n-3 lorsque n=4p+2
S(32n+6)
= 15 qui correspond à S(4(8p+1)+2) = 15 et donc S(4n+2)=15
lorsque n est de la forme n=8p+1
Ces deux derniers exemples, (et il y
en a d’autres), te montrent que ce n’est pas évident pour 4n+2 et qu’il
n’y a pas de formule unique simple pour S(4n+2)
Je pourrais reprendre la liste des
formules, mais je préfère généraliser, tu as remarqué 4, 8, 16, 32... les puissances de 2 et 3, 7, 15 ... les puissances de 2
moins un...
DÉMO :
Soient S(n)+S[n+1+S(n)]=n
et les deux formules (k=2,3,4...)
S(2^k
* n+ 2^(k-2) -2 )= 2^(k-1) - 1
S(2^k
* n + 3* 2^(k-2) -2) = 2^k * n -2^(k-2) -1
En débutant à k = 2 on a la formule S(4n-1) = 1. La démonstration est une récurrence.
Ensuite c’est un jeu d’enfant de
montrer qu’il n’y a aucune collision entre ces formules (en nombre infini) et que
ces formules suffisent à remplir tout l’espace (définir la suite S(n) pour tout
entier n>0)
__________
[Éric to SeqFans,
later] :
For an increasing sequence with the same property
("seed+bean=n"):
S = 0, 1,
1, 1, 2, 3, 3, 3, 3, 3, 4, 5, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 8, 9, 10, 11, 12,
13, 14, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 31, 31, 31, 31, 31,
...
Best,
É.
__________
[Jean-Paul
Davalan]:
(...)
Je viens de rédiger un petit
programme, j’ai fait cette fois quelques essais.
Il y a d’autres suites qui se
définissent comme l’autre (c.-à-d. S(4*n-1) = 1),
ce sont S(4*n-1)
=5 ou S(4*n-1) =9 ... Ce qui suffit à les définir, quitte à commencer les suites
avec n négatif pour la construction et en ne gardant ensuite que les termes
pour n positif (n>=0) ou pour n>0, (au choix, selon ses préférences).
Il y a effectivement des suites
croissantes, pas strictement croissantes mais pas constantes non plus. La
démonstration devrait être simple (mais je n’en suis plus si sûr). Plus simple
- sauf imprévu - que pour les précédentes qui étaient définies par S(4*n-1)=4*Constante+1.
En débutant à n=1 avec S(1)=0 :
0 1 1 1 2 3 3 3
3 3 4 5 6 7 7 7 7 7 7 7 7 7 8 9 10 11 12 13 14 15 15 15 15
15 15 15
15 15 15
15 15 15
15 15 15
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 31 31 31
31 31 31
31 31 31
31 31 31
31 31 31
31 31 31
31 31 31
31 31 31
31 31 31
31 31 31
31 31 32 33 34 35 36 37 38
39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 63 63
63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104
105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124
125 126 127 127 127 127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
127 127 127
128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147
148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167
168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187
188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207
208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227
228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247
248 249 250 251 252 253 254 255 255 255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
255 255 255
256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275
276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295
296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315
316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335
336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355
356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375
376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395
396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415
416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435
436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455
456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475
476 477 478 479 480 481 482 483 484 485 486 487 488 489
En voici une autre qui débute à n=3
en prenant S(3)=1 :
_ _ 1 2 2
2 2 3 4 5 5 5 5 5 5 5 6
7 8 9 10 11 11 11 11 11 11
11 11 11
11 11 11
11 12 13 14 15 16 17 18 19 20 21 22 23 23 23 23
23 23 23
23 23 23
23 23 23
23 23 23
23 23 23
23 23 23
23 23 23
24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 47 47 47
47 47 47
47 47 47
47 47 47
47 47 47
47 47 47
47 47 47
47 47 47
47 47 47
47 47 47
47 47 47
47 47 47
47 47 47
47 47 47
47 47 47
47 47 47
48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73
74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 95 95 95
95 95 95
95 95 95
95 95 95
95 95 95
95 95 95
95 95 95
95 95 95
95 95 95
95 95 95
95 95
Ou encore en partant de
S(6)=2 :
_ _ _ _ _ 2 3 4 4 4 4 4 4 5 6 7 8 9 9
9 9 9
9 9 9
9 9 9
10 11 12 13 14 15 16 17 18 19 19 19
19 19 19
19 19 19
19 19 19
19 19 19
19 19 19
19 19 19
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 39
39
Les propriétés de toutes ces suites
de la famille doivent être intéressantes. Là aussi, il faudrait que je rédige
les démonstrations. À partir de mercredi j’aurai peut-être le temps de le
faire.
Une remarque en passant, à ces
constructions sont associées des bijections de N vers N^2, comme je l’avais
aussi remarqué pour ta suite sur les décimations.
__________
[Aai]:
Illustrating
another process of generating sequence S
=====================================================
Looking at S
with 0-based indices we have:
This color is for J
language
S=0,1,1,1,2,3,1,3,6,3,1,5,10,7,1,3,14,7,1,13,18,7,1,3,22,11,1,21,26,15,1,3,30,7,
n= 1,2,3,4,5,6,7,8,9,1,1, 1,1,1,1, 1,1,1, 1,
2,2,2,2, 2, 2,2, 2, 2, 2,3,3, 3,3,
0 1 2 3 4 5
6 7 8 9 0 1 2 3
4 5 6 7
8 9 0 1 2 3
Positions of
basic 1’s:
+/\1 1, 10$4
1 2 6 10 14 18 22 ...
These
indices are also elements of sequence S at positions: 2+ +/\1 1, 10$4
3 4 8 12 16 20 24 28 32 36 40 44 ...
So we can
build this sequence by:
starting with a virgin sequence of 0’s: ]z=.0$~y=.58
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ...
indices of 1’s: k= . +/\1 1, 4$~<.4%~y-2
assigning 1’s: ] z=. 1 k }
z
0 1 1 0 0 0 1 0 0
0 1 0 0 0
1 0 0 0 1 0 0 0 1 0 0
0 1 0 0 0
1 0 0 0 1 0 0 0 ...
assigning indices of the basic 1’s: ] z=. (}:k) (}:2+k) }z
0 1 1 1 2 0 1 0 6 0 1 0 10 0 1 0 14 0 1 0 18 0 1 0 22 0 1 0 26 0
1 0 30 0 1 0 34 0 1 ...
There’s
another set of numbers that can be found at regular positions, namely:
3 7 15 31... or
2^2 - 1, 2^3 -1, etc.
Calculating
principle to obtain the positions of these numbers:
3: starting
index 5 = 2 * 3 - 1
and then: 7 9 15 23 31 39 ...
diff: 2 2
6 8
8 8 8 ...
7: starting
index 13 = 2 * 7 - 1
and then: 17
21 33
49 65 ...
diff: 4 4 12 16 16 16 ...
15: starting
index 29 = 2 * 15 - 1
and then: 37 45
69 101 133
165 197 ...
diff: 8 8 24 32 32 32 32 ...
So for the numbers
e = 3, 7, 15, ... with e = 2^(1+i) - 1 and i = 1,2,3,... we have diff
sequences:
2 2 6 8 8 8 8
... basic sequence
Doubling the
values for every next 2^(1+i) - 1
... resulting in index-sequences: +/\(1-~2*1-~2^i+1), +~^:(i-1) 2 6 8 8 8 8
...
Examples:
3:
+/\(1-~2*1-~2^i+1),
+~^:(i-1) 2 2 6, 10$8 [ i=.1
5 7 9 15 23 31 39 47 55 63 71 79 87 95
7:
+/\(1-~2*1-~2^i+1),
+~^:(i-1) 2 2 6, 10$8 [ i=.2
13 17 21 33 49 65 81 97 113 129 145 161 177
193
Etc.
After this
procedure there are still some ‘0’-holes left, other than the first one.
0 1 1 1 2 3 1 3 6 3 1 0 10 7 1 3 14 7 1 0 18 7 1 3 22 0 1 0 26 15 1 3 30 7 1 0 34 15 1 3 38 0 1 0 42 15 1 3 46 7 1 0 50 0 1 3 54 0
Compare with
the original sequence S:
6 10 $ S
0 1 1 1 2 3 1 3 6 3 1 0 10 7 1 3 14 7 1 0 18 7 1 3 22 0 1 0 26 15 1 3 30 7 1 0 34 15 1 3 38 0 1 0 42 15 1 3 46 7 1 0 50 0 1 3 54 0
0 1 1 1 2 3 1 3 6 3 1 5 10 7 1 3 14 7
1 13 18 7 1 3 22 11 1 21 26 15 1 3 30 7 1 29 34 15 1 3 38 27 1 37 42 15 1 3 46
7 1 45 50 23 1 3 54 43
Remaining
numbers to fill these holes are:
5 11 13 21
23 27 29 37 43 45
Solution to
calculate and fill the remaining ‘holes’:
find first index
i of a hole: i
find first index
j where i == 1 + j + [j]
calculate and fill hole [i] [i] = 1 +
j - [j]
repeat until done:
all holes filled.
--
Met vriendelijke groet,
=@@i
Nice, Aai!
__________
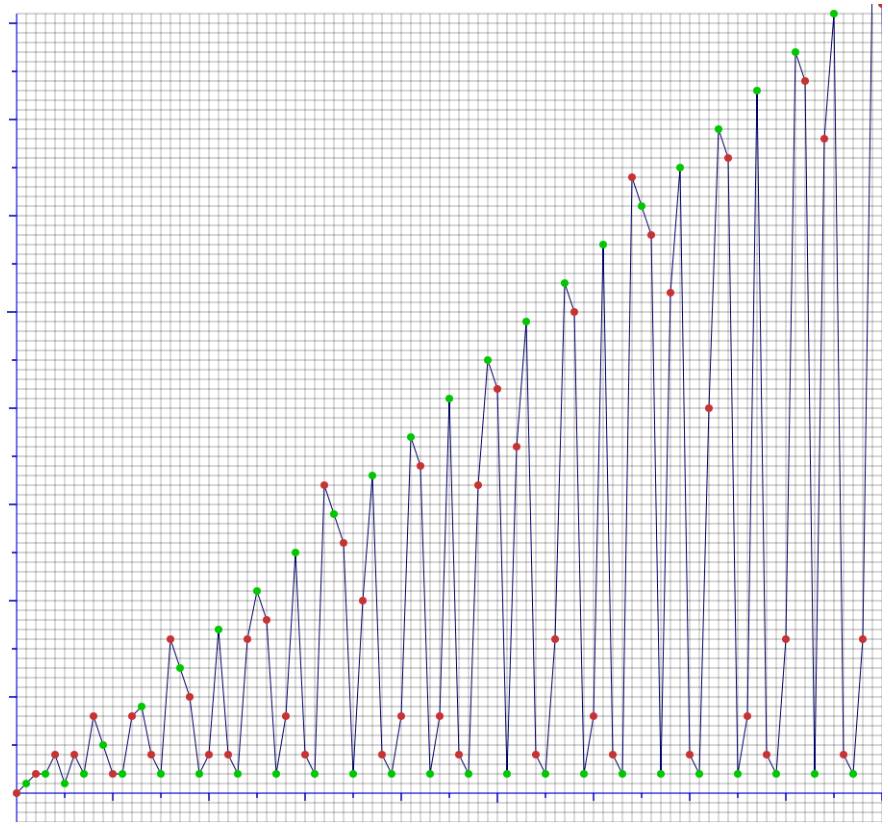
Voici le graphique de la suite
qui ouvre cette page, généré par le programme de Jean-Paul
Davalan (bouton EA1):
__________
Merci Jean-Paul & Aai,
à+
É.
(dernière mise à jour : 14 décembre 2011)