Playing with digital roots
(DR, in short)
“The digital root
(also repeated digital sum) of a
number is the number obtained by adding all the digits, then adding the digits of
that number, and then continuing until a single-digit number is reached. For
example, the digital root of 65536 is 7, because 6 + 5 + 5 + 3 + 6 = 25
and 2 + 5 = 7.”
Now, what would be
the digital root of DIGITAL ROOT? I’ve used Gef’s Gematron
(a=1, b=2, c=3,... z=26) and found 4. And this 4 is
the same figure as the DR of DR (and
also of dumb, lame, imbecile, I know!)
What about the DR
of a few (English) number names? (Note that the DR of a sum of elements is the
same as the DR of the concatenation of the said elements):
ONE [7]
TWO [4]
THREE [2]
FOUR [6]
FIVE [6]
SIX [7]
SEVEN [2]
NINE [6]
TEN [3]
ELEVEN [9]
TWELVE [6]
THIRTEEN [9]
FOURTEEN [5]
FIFTEEN [2]
SIXTEEN [6]
SEVENTEEN [1]
EIGHTEEN [1]
NINETEEN [5]
TWENTY [8]
...
We see that no
integer is its own digital root (in English); what about a sequence of number
names divisible by its own DR? [This is not A064807, of
course (“Numbers which are divisible by their digital root”), we deal here with
words]. The first integers matching
the requisite are TWELVE [6], then SEVENTEEN [1], etc.:
SDR =
12,17,18,23,25,27,30,...
__________
More seriously (?)
now; the few (complicated? artificial?) sequences hereunder refer somehow to
themselves.
TDR, the first one,
is monotonically increasing: “a(n) and the sum
[a(1)+a(2)+a(3)+... a(a(n))] share the same DR”.
TDR = 1, 3, 8, 9, 10,
11, 12, 17, 19, 28, 37, 46, 47, 48, 49, 50, 54, 55, 64, 65, 66, 67, 68, 69, 70,
71, 72, 73, 74,...
TDR was build with the help of
this array, where n goes from 1 to
infinity; TDR
is the sequence; Q is the cumulative
sum of TDR’s
terms; DR is the digital root of Q (the underlined terms of Q are also the successive digital roots
of TDR and the digital roots of
the 3 terms just above them):
nDR=1|2|
3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13|
14| 15| 16| 17| 18| 19| 20| 21| 22| 23| 24| 25| 26|
27| 28| 29|...
TDR=1|3| 8| 9|10|11|12|17|19| 28| 37|
46| 47| 48| 49| 50| 54| 55| 64| 65| 66| 67| 68| 69| 70| 71|
72| 73| 74|...
QDR=1|4|12|21|31|42|54|71|90|118|155|201|248|296|345|395|449|504|568|633|699|766|834|903|973|1044|1116|1189|1263|...
DRDR=1|4| 3| 3| 4|
6| 9| 8| 9| 1| 2|
3| 5| 8| 3| 8| 8| 9| 1| 3|
6| 1| 6|
3| 1| 9|
9| 1| 3|...
In building TDR, the smallest integer not present
and not leading to a contradiction was used. The sequence can be read like
this:
- Pick up any term of TDR, for instance 12; now the digital root
of 12 (which is 3) is the same as the digital root of the sum of the first 12
terms of the sequence (which is 201, with digital root —>3)
- Another example is 19: the DR of 19 (—>1) is the same as
the DR of the sum of the first 19 terms of TDR (568 —>1).
-----
UDR is the same
sequence, dropping the ‘increasing’ constraint (we thus keep this definition
for UDR:
: “a(n) and the sum [a(1)+a(2)+a(3)+... a(a(n))] share the same DR”.
UDR = 1, 3, 8, 5, 6,
10, 9, 11, 19, 28, 37, 13, 16, 15, 23, 46, 18, 20, 21, 26, 55, 24, 32, 64, 27,
29, ...
UDR was build with the same kind
of array:
nDR=1|2|
3| 4| 5| 6| 7| 8| 9| 10| 11|
12| 13| 14| 15| 16| 17| 18| 19| 20| 21|
22| 23| 24| 25| 26| 27| 28| 29|...
UDR=1|3| 8| 5| 6|10| 9|11|19| 28| 37|
13| 16| 15| 23| 46| 18| 20| 21| 26| 55| 24| 32| 64| 27| 29| 73| 82| 91|...
QDR=1|4|12|17|23|33|42|53|72|100|137|150|166|181|204|250|268|288|309|335|390|414|446|510|537|566|639|721|812|...
DRDR=1|4| 3| 8| 5| 6| 6| 8|
9| 1|
2| 6| 4| 1| 6|
7| 7| 9|
3| 2| 3|
9| 5| 6|
6| 8| 9|
1| 2|...
UDR is the sequence showing the
lowest quantity of missing integers (those are the not underlined n’s above: 2,4,7,12,...)
To understand this sequence, just read it like
this:
- Select any term of UDR, for instance 11; now the digital root
of 11 (—>2) is equal to the digital root of the sum of the first 11 terms of
UDR
(which is 137 —> 1+3+7=11 —> 1+1 —> 2).
- Try 28; the digital root of 28 (—>1) is the digital root of the
sum of the first 28 terms (721—>1); etc.
In building the sequence from scratch, always
use the smallest integer not used so far and not leading to a contradiction.
_________
The same idea is at work hereunder, but involves
prime numbers:
VDR is a re-ordering of the
Primes where a(n) and a(a(n)) share the same DR:
VDR = 2, 11, 3, 5,
23, 7, 43, 13, 17, 19, 29, 41, 31, 61, 67, 71, 53, 73, 37, 83, 97, 107, 113,
127, ...
VDR was build with a simple
two-line array where an (underlined) Prime in n has the same DR as the term below it, term which was the smallest
unused so far in building the sequence:
nDR=1| 2|
3| 4| 5| 6| 7| 8| 9|10|11|12|13|14|15|16|17|18|19|20|21|
22| 23| 24| 25| 26| 27| 28|29| 30| 31| 32| 33|...
VDR=2|11| 3| 5|23| 7|43|13|17|19|29|41|31|61|67|71|53|73|37|83|97|107|113|127|137|139|149|181|47|191|193|197|223|...
VDR is the lexicographically
first such sequence and could be read like this:
- Choose any term in VDR, for
instance 11; now
the digital root of 11 (—>2) is the same as the digital root of the 11th
term of the sequence (which is 29, with DR —>2).
- A try with 23; the DR of 23 is 5 and
the DR of the 23rd term (113) is 5 too.
-----
Breaking News (March 3rd, 2010):
Georges Brougnard has just corrected VDR and sent a
nice graph of the first 500 terms:
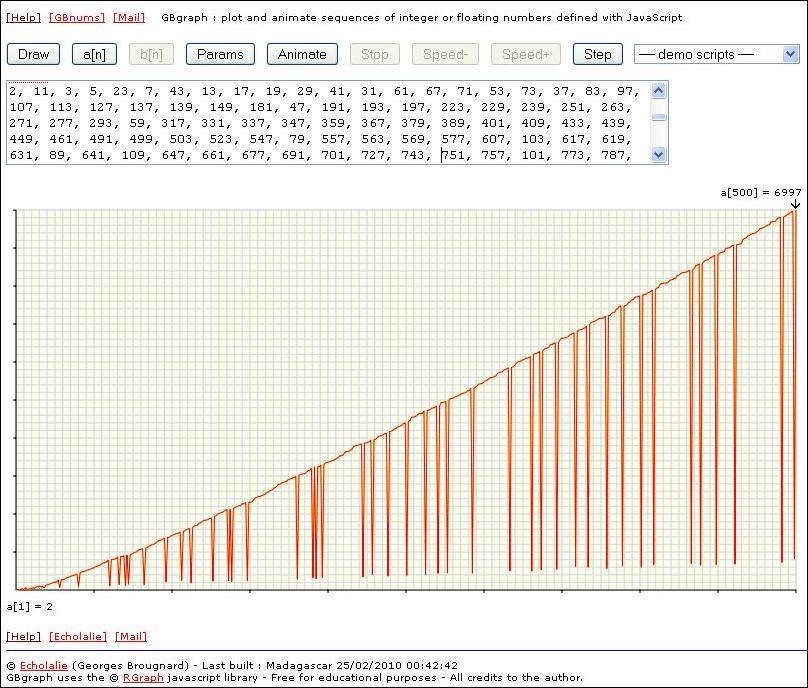
Here are the 500 first terms of VDR computed
by Georges:
VDR = 2, 11, 3, 5, 23, 7, 43, 13, 17, 19, 29, 41, 31, 61, 67, 71, 53, 73, 37, 83,
97, 107, 113, 127, 137, 139, 149, 181, 47, 191, 193, 197, 223, 229, 239, 251,
263, 271, 277, 293, 59, 317, 331, 337, 347, 359, 367, 379, 389, 401, 409, 433,
439, 449, 461, 491, 499, 503, 523, 547, 79, 557, 563, 569, 577, 607, 103, 617,
619, 631, 89, 641, 109, 647, 661, 677, 691, 701, 727, 743, 751, 757, 101, 773,
787, 797, 827, 829, 839, 859, 881, 907, 911, 919, 941, 947, 151, 967, 971, 991,
1013, 1019, 1033, 1039, 1049, 1063, 179, 1069, 1097, 1109, 1123, 1129, 131,
1153, 1181, 1187, 1193, 1231, 1237, 1259, 1279, 1283, 1289, 1303, 1319, 1327,
163, 1361, 1367, 1399, 1409, 1423, 1429, 1451, 1471, 1481, 173, 1483, 157,
1493, 1523, 1531, 1543, 1553, 1567, 1583, 1597, 1607, 167, 1613, 1619, 1627,
1657, 1699, 1709, 1721, 1723, 1733, 1747, 1759, 1789, 1801, 1823, 1831, 1847,
1879, 1889, 1913, 1949, 1951, 1973, 1979, 1993, 1999, 2029, 2039, 2053, 2063,
2069, 2099, 199, 2113, 2129, 2137, 2141, 2143, 2179, 2203, 2207, 2239, 227,
2267, 211, 2269, 2273, 2297, 233, 2311, 2341, 2351, 2357, 2371, 2381, 2383,
2411, 2417, 2441, 2467, 2473, 2477, 2521, 2549, 2551, 2557, 2579, 2591, 2647,
2657, 2663, 2671, 2677, 2687, 241, 2707, 2711, 2719, 2731, 2753, 283, 2767, 2777,
2801, 2833, 2837, 2843, 2857, 2879, 2887, 257, 2917, 2927, 2939, 2969, 2971,
2999, 3011, 3019, 3041, 3067, 3079, 269, 3109, 3119, 3181, 3187, 3191, 3203,
3229, 3251, 3253, 3257, 3299, 281, 3307, 3313, 3319, 3347, 3359, 3361, 3389, 307,
3391, 3449, 3457, 3461, 3469, 313, 3499, 3527, 3529, 3539, 3559, 3571, 3583,
3593, 3617, 3623, 3631, 3643, 3673, 3677, 3709, 311, 3719, 3733, 3761, 3793,
3797, 3803, 3823, 3851, 3853, 3881, 3907, 3911, 3919, 3931, 3947, 3989, 4003, 4013,
4019, 4051, 4057, 4079, 4091, 353, 4099, 4111, 4139, 4177, 4201, 4211, 4217,
4241, 4243, 4271, 4273, 4283, 4297, 349, 4339, 4349, 4363, 4373, 4397, 373,
4409, 4441, 4447, 4457, 4481, 4519, 4523, 4547, 4549, 383, 4561, 4603, 4637, 4639,
4643, 4651, 4663, 4691, 4703, 4729, 4733, 431, 4759, 4787, 4793, 4801, 4817,
4831, 4861, 421, 4889, 4931, 4937, 4951, 4957, 4987, 4999, 5003, 5009, 5011,
5039, 397, 5051, 5059, 5099, 5113, 5119, 5171, 5179, 5227, 5231, 443, 5233, 5237,
5261, 5297, 5309, 5347, 5351, 5393, 5399, 5407, 5413, 419, 5437, 5441, 5449,
5471, 5479, 5501, 5521, 463, 5531, 5563, 5573, 5623, 5647, 5651, 5653, 5657,
5659, 5701, 5711, 5717, 5741, 5743, 5791, 5801, 5821, 5843, 5849, 5851, 5857, 5879,
5881, 487, 5903, 5923, 5981, 5987, 6007, 457, 6011, 6047, 6073, 6079, 6089,
6121, 6131, 6151, 6163, 467, 6173, 6197, 6217, 6221, 6229, 6287, 6299, 6301,
6311, 6343, 6353, 479, 6359, 6367, 6373, 6379, 6451, 6473, 6481, 6521, 6529, 6551,
6563, 6571, 6577, 6599, 6619, 6659, 6661, 6673, 6689, 6709, 6719, 6733, 6779,
6781, 6791, 6793, 6841, 6857, 6863, 509, 6869, 6883, 6907, 6917, 6947, 6967,
6977, 571, 6997,...
If someone needs more terms (for instance 666)
just copy/paste the hereunder blue script into Georges’s
GBgraph (which
can be found here), then
change manually aDim=100 into aDim=666, then click “Draw” to plot
and “a(n)” to see the 666 integers wanted:
![]()
aDim=100;
interval(1,aDim);
if(inInit)
{
aList = new Array(0);
function DR(n) {if(n <10) return n; return DR(digitsum(n));}
function nextDRprime(dr) {for (var p = notused(1);; p = notused(p))
if(isprime(p))
if(dr == -1 || DR(p) == dr) return p;
}
for(i=1;i<=aDim;i++)
if(aList[i] == undefined)
{
use(aList[i] = nextDRprime(-1))
;
if(aList[i] != i) use(aList[aList[i]] = nextDRprime(DR(aList[i])));
}
}
-----
WDR has a slightly different
definition from VDR
– which makes all the difference: we allow now the presence of composite
numbers – whose quantity has been maximized here.
WDR definition: a(a(n)) is a Prime sharing a(n)’s DR.
Again, a two-line array suffices:
nDR=_1|2|3| 4|5|6|7| 8|9|10|11|12|13|14|15|16|17|18|19|20|21|22|23|24|25|26|27| 28|29|30| 31|32|33|34|35| 36|...
WDR=19|2|3|13|5|1|7|17|4|37|11|
8|31|23|10|43|53|14|73|29|16|67|41|20|61|71|22|109|47|25|103|59|26|79|28|109|...
WDR is the sequence showing the
lowest quantity of missing integers; those missing integers are the multiples
of 3 (except 3 itself), as the DR of a prime >3 is never 3, 6 or 9.
WDR is the lexicographically
first such sequence and could be read like this:
- pick up any term in WDR, for
instance the first one, 19;
now the digital root of 19 (—>1) is the same as the digital root of the 19th
term of the sequence, which is a prime (indeed, the 19th term is 73,
prime with DR —>1).
- a
try with 17; the DR
of 17 is 8 and the DR of the 17th term (53, a Prime) is 8 too.
As usual, in building the sequence from scratch,
always use the smallest integer not present so far in WDR and not leading to a
contradiction.
Best,
É.
_______________________
Back to the Sweet
page.
Back
to main page.