Fibonaccit
Hello SeqFans,
start S with 0 and 1. Now:
- the
next term of S is the sum of the last two not yet summed digits of S:
S=0,1,1,2,3,5,8,13,9,4,12,13,5,3,3,4,...
Does S end in a loop?
Best,
….
____________
[Jim Nastos]:
Hi Eric,
†Can you
explain to me why the 4th term is 2?
J.
[Eric]:
Hi Jim,
0 and 1 is 1
1 and 1 is 2
1 and 2 is 3
2 and 3 is 5
3 and 5 is 8
5 and 8 is 13
8 and 1 (the first digit of "13") is
9
1 and 3 (the second digit of "13") is
4
3 and 9 is 12
...
[Lars
Blomberg]:
Hello Eric,
Thank you for a Saturday morning challenge. Well,
it was not terribly difficult, but fun!
Extending the series to 10^8+2, I have found no
loop.
Here is a histogram of the series:
0††† 1
1††† 7745040
2††† 6601748
3††† 5716833
4††† 7690317
5††† 7277147
6††† 7621188
7††† 7081774
8††† 7431603
9† †13251816
10† †7097479
11† †3410444
12† †3583979
13† †3099546
14† †3321937
15† †1706873
16† †1778854
17† ††704563
18† †4878860
Note the entries for 9 and 17.
Regards,
Lars
[Maximilian
Hasler]:
I did not see a loop in the first 1000 terms
but maybe there is a kind of "chaotic attractor" in the form of a subsequence
starting 7,7,8,8,9,9,5,5,1,6,13,14,... of which an increasingly longer piece of
initial terms repeats infinitely often: I have put *** at the beginning of that subsequence in
the printout below.
0, 1, 1, 2, 3, 5, 8, 13, 9, 4, 12, 13, 5, 3, 3,
4, 8, 8, 6, 7, 12, 16, 14, 13, 8, 3, 3, 7, 7, 5, 5, 4, 11, 11, 6, 10, 14, 12, 10,
9, 5, 2, 2, 2, 7, 7, 1, 1, 5, 5, 3, 3, 1, 9, 14, 7, 4, 4, 9, 14, 8, 2, 6, 10, 8,
6, 4, 10, 10, 5, 11, 11, 8, 13, 10, 5, 12, 10, 8, 7, 1, 8, 14, 10, 5, 1, 1, 1, 5,
6, 2, 2, 2, 9, 9, 4, 4, 1, 5, 6, 3, 3, 1, 8, 15, 8, 9, 9, 5, 5, 1, 5, 6, 2, 2, 6,
11, 8, 4, 4, 11, 18, 13, 8, 5, 6, 11, 9, 6, 4, 9, 9, 6, 13, 17, 18, 14, 10, 6, 6,
11, 8, 4, 8, 7, 2, 9, 12, 8, 5, 2, 2, 9, 9, 4, 11, 13, 11, 7, 2, 10, 15, 10, 13,
18, 15, 7, 4, 4, 8, 8, 9, 9, 5, 5, 1, 6, 12, 7, 2, 9, 12, 12, 15, 9, 11, 10, 3,
10, 13, 7, 4, 11, 18, 13, 5, 2, 2, 4, 4, 2, 8, 9, 3, 1, 1, 6, 6, 1, 1, 4, 4, 9,
9, 6, 12, 11, 8, 12, 16, 17, 18, 14, 10, 6, 7, 7, 3, 9, 9, 11, 10, 3, 3, 3, 3, 6,
14, 10, 2, 2, 1, 3, 4, 1, 1, 4, 10, 11, 5, 2, 2, 9, 9, 4, 8, 7, 4, 6, 8, 6, 10,
17, 12, 4, 2, 7, 12, 7, 2, 5, 8, 13, 18, 15, 7, 3, 3, 2, 9, 9, 3, 3, /***/ 7, 7, 8, 8, 9, 9, 5,
5, 1, 6, 13, 14, †10, 12, 18, 10, 2, 2, 1,
3, 6, 6, 6, 9, 7, 5, 5, 1, 2, 4, 3, 4, 7, 5, 2, 5, 5, 1, 1, 2, 6, 7, 4, 11, 18,
13, 12, 15, 11, 10, 14, 14, 7, 1, 1, 8, 8, 3, 6, 6, 9, 8, 3, 9, 9, 7, 13, 9, 4,
4, 9, 9, 6, 12, 10, 6, 5, 11, 18, 12, 6, 10, 14, 15, 16, 17, 18, 14, 10, 6, 7, 7,
4, 4, 5, 5, 1, 1, 3, 3, 9, 9, 1, 2, 4, 3, 4, 9, 12, 12, 15, 16, 12, 10, 6, 3, 6,
7, 7, 11, 12, 7, 7, 10, 6, 2, 3, 8, 13, 11, 5, 2, 2, 9, 9, 4, 4, 3, 3, 6, 6, 2,
2, 1, 1, 5, 5, 5, 11, 8, 2, 9, 16, 11, 9, 12, 15, 17, 11, 12, 18, 16, 8, 4, 12,
13, 8, 13, 18, 15, 7, 3, 3, 1, 6, 11, 6, 2, 2, 9, 9, 3, 8, 7, 1, 1, 5, 5, 6, 6,
/***/ 7, 7, 8, 8, 9,
9, 5, 5, 1, 6, 13, 14, †11, 8, 9, 10, 6, 2,
4, 6, 12, 18, 10, 3, 6, 7, 7, 13, †10, 3,
3, 3, 3, 6, 6, 7, 7, †3, 3, 1, 6, 9, 9, 13,
14, 8, 2, 2, 3, 9, 14, 8, 1, 6, 8, 5, 11, 9, 4, 4, 2, 6, 7, 4, 11, 18, 13, 8, 7,
6, 9, 12, 8, 4, 3, 2, 6, 10, 10, 6, 2, 9, 10, 11, 10, 7, 7, 2, 10, 10, 3, 3, 6,
6, 8, 8, 2, 2, 3, 3, 9, 9, 7, 14, 12, 5, 3, 3, 4, 11, 9, 4, 4, 9, 9, 6, 12, 10,
6, 4, 7, 7, 2, 7, 8, 4, 11, 18, 12, 11, 15, 8, 2, 6, 10, 11, 12, 13, 14, 15, 16,
17, 18, 14, 10, 6, 7, 7, 4, 4, 5, 5, 2, 9, 17, 10, 1, 6, 8, 6, 10, 7, 3, 3, 9, 9,
1, 3, 9, 13, 14, 8, 4, 4, 1, 3, 6, 6, 6, 9, 12, 13, 14, 10, 6, 4, 7, 15, 18, 10,
4, 4, 5, 12, 10, 4, 5, 12, 10, 5, 12, 9, 7, 14, 13, 6, 2, 10, 13, 8, 6, 8, 13, 11,
5, 2, 2, 9, 9, 4, 11, 15, 13, 15, 10, 3, 10, 12, 7, 5, 8, 7, 1, 1, 1, 6, 8, 11,
10, 1, 1, 2, 2, 1, 7, 14, 9, 3, 1, 1, 1, 3, 6, 9, 12, 14, 16, 10, 4, 5, 6, 12, 18,
16, 8, 5, 5, 3, 7, 8, 6, 7, 5, 2, 10, 13, 8, 13, 18, 15, 7, 3, 3, 1, 6, 10, 11,
14, 9, 9, 15, 12, 5, 2, 2, 9, 9, 3, 3, 2, 2, 6, 13, 10, 8, 7, 1, 1, 2, 2, 3, 3,
4, 4, 5, 5, 6, 6, /***/
7, 7, 8, 8, 9, 9, 5, 5, 1, 6, 13, 14, †11,
8, 9, 10, 7, 11, 10, 8, 8, 1, 1, 7, 14, 14, 7, 1, 7, 10, 6, 12, 18, 10, 4, 12, 10,
4, 4, 5, 12, 12, 8, 5, 4, 9, 12, 12, 15, 10, 3, 3, 4, 4, 5, 5, 1, 6, 10, 11, 8,
6, 6, 9, 9, 1, 4, 8, 9, 6, 3, 3, 1, 4, 9, 6, 3, 3, 1, 5, 6, 3, 11, 16, 8, 5, 5,
4, 9, 8, 3, 1, 1, 4, 11, 14, 14, 9, 4, 4, 2, 6, 7, 4, 11, 18, 13, 5, 2, 2, 6, 6,
4, 4, 6, 6, 1, 3, 4, 1, 1, 3, 9, 12, 13, 15, 8, 2, 2, 7, 14, 9, 2, 2, 1, 1, 2, 3,
4, 3, 8, 8, 5, 13, 12, 4, 2, 2, 4, 9, 15, 10, 3, 3, 5, 5, 7, 7, 1, 4, 9, 11, 7,
3, 3, 9, 9, 7, 14, 13, 10, 8, 10, 15, 14, 13, 12, 7, 3, 1, 1, 4, 11, 9, 4, 4, 9,
9, 6, 12, 10, 6, 4, 7, 7, 1, 1, 2, 2, 5, 13, 18, 10, 6, 6, 3, 7, 7, 4, 11
(PARI)
digonacci(n,d=[0,1])={print1("0,1");for(i=2,n,print1(","a=d[1]+d[2]);
d=concat(vecextract(d,"^1"),digits(a)))}
[Hans
Havermann]:
Maximilian Hasler:
> I did not see a loop in the first 1000
terms but maybe there is a kind of
> "chaotic attractor" in the form
of a subsequence starting 7,7,8,8,9,9,5,5,1,6,13,14,...
Here is a slightly different approach to
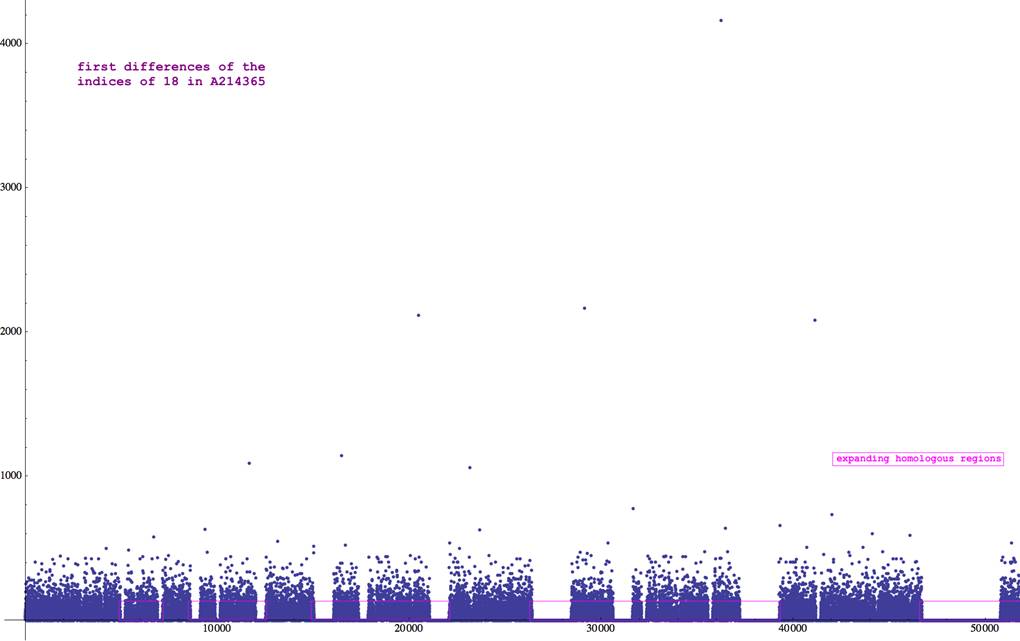
finding quasi-regularity in Ericís sequence. I calculated a large number of
terms of the sequence, the positions therein of the number 18 and the first
differences of these position numbers. Here is a graph:
Those
varying-length stretches where the graph drops down to the axis are
consecutive ones, representing consecutive eighteens in the original sequence.
[Zak Seidov]:
I donít know about cycle but s(78532..78532+65)
= sixty six 9ís.
Conjecture: there may be arbitrary long similar
runs.
Zak.
[Hans Havermann]:
Lars Blomberg:
> I have found
no loop within the first 10^8 terms.
Hey
Lars. :)
As a
non-mathematician I canít quite formalize a proof, but consider those
consecutive 18s mentioned in my previous post. A stretch of k 18s will generate
roughly 2k 9s in the corresponding summed-digits list, which
in turn generate 2k 18s. Thus the number of consecutive 18s will grow
without limit and no loops are possible.
[Franklin T. Adams-Watters]:
Thatís a fine proof.
[Maximilian Hasler]:
FYI, this is now http://oeis.org/A214365.
Any comments &
contributions are welcome.
__________
Any thanks to all contributors Ė case closed!
Best,
….
__________
P.-S.
[…ric, mostly to
himself]:
Voici quelques nombres N qui, subissant le
traitement "Fibonaccit", produisent (se
greffent sur) S :
N : 11, 12, 23,
35, 58, 813, 139, 394, 9412, 41213, 12135, 21353, 13533, ...
S = 0, 1, 1, 2, 3, 5, 8, 13, 9, 4, 12, 13, 5, 3, 3, 4, ...
Quelle serait la suite N des nombres qui se
greffent sur S ? 2013 fait-il partie de cette suite N ?
Sweet is there.