Prime’s Rank
(où l’on remplace des facteurs premiers par
leur rang)
L’histoire de Prime’s Rank commence par un courrier privé adressé à Georges Brougnard, fin janvier 2009 :
« Hello Georges -- je viens de tomber sur une chouette idée (qui me fera
dormir mal ;-)
- je cherche depuis longtemps un jeu genre
Syracuse (si un
nombre est pair, divise-le par 2 ; s'il est impair, multiplie-le par 3 et
ajoute 1 au résultat ; recommence)
- le problème est de trouver une astuce
qui permette (comme pour Syracuse) de monter, de descendre, de remonter, de
s'effondrer finalement sur 1 — éventuellement de tomber sur des points fixes,
sur des boucles, etc.
- j'ai fait chou-blanc jusqu'ici. Mais
soudain... Attention, un poil compliqué !
a) on part d'un nombre (p.ex. 6)
b) on le décompose en facteurs premiers :
6 = 2.3 (facteurs en ordre croissant)
c) on écrit sous les facteurs leur rang dans la suite des premiers:
facteurs : 2.3
rangs : 1 2 (car le facteur 2 est le 1er
nombre premier et le facteur 3 le 2e)
d) on concatène ces rangs pour former un
nouveau nombre : 12
e) on recommence la procédure en (b).
REMARQUE : il se peut que le nombre
obtenu par concaténation soit premier ; on le remplace alors par son propre
rang dans la suite des premiers — et on recommence la procédure à partir de là.
Exemple de ce cas précis avec 4
a) 4
b) 4 = 2.2
c)
1 1
d) 11 (résultat de la concaténation) est
remplacé par 5 (car 11, indécomposable en facteurs, est le 5e
premier)
a) 5 -> est remplacé par 3
a) 3 -> est remplacé par 2
a) 2 -> est remplacé par 1 -- STOP
---
Je développe ici le cas de 6 (qui est un
extraordinaire candidat -- si je ne me suis pas trompé !) :
- le nombre ci-dessous "entre
guillemets anglais" est la concaténation des rangs des facteurs premiers écrits avant lui ;
- ce nombre entre guillemets est décomposé
juste après la flèche en ses facteurs premiers (par ordre croissant), séparés
par des points ;
- ensuite on recommence la
procédure :
6 -> 2.3 = "12" -> 2.2.3 = "112" ->
2.2.2.2.7 = "11114" -> 2.5557 = "1733" ->
"270" (car 1733 étant premier, on le remplace par son rang) ->
2.3.3.3.5 = "12223" -> 17.719 = "7128" ->
2.2.2.3.3.3.3.11 = "11122225" -> 5.5.23.23.29.29 =
"33991010" ... etc.
(...)
Les nombres premiers qui appartiennent à
la suite de Neil n°A007097
tombent tous sur 1 (par définition). Les composites qui passent par un des
nombres de A007097 (cette même suite baptisée "Primeth
recurrence") retombent du coup aussi sur 1 (ils
sont « attirés » dans le vortex !)
Y a-t-il un nombre qui ne retombe pas sur
1 ? (qui entre dans une boucle, p.ex.)
Bonne nuit !
;-)
à+
E. »
---
Dès réception de ce message, Georges Brougnard se rua sur GBnums, son boulier automatique
(disponible gratuitement ici), et
calcula les suites commençant par 4, 5, 6, 7, 8, 9, 10 et quelques
autres :
->départ(4) : 4, 11, 5, 3, 2, 1 STOP
->départ(5) : 5, 3, 2, 1 STOP
->départ(6) : 6, 12, 112, 11114, 1733, 270, 12223,
7128, 11122225, 33991010, 13913661, 2107998, 12222775, 33910130, 131212367,
56113213, 6837229, 4201627, 266366, 112430, 131359, 7981, 969, 278, 134, 119,
47, 15, 23, 9, 22, 15 CYCLE
->départ(7) : 7, 4, 11, 5, 3, 2, 1 STOP
->départ(8) : 8, 111, 212, 1116, 112211, 52626,
124441, 28192, 11111152, 111165448, 1117261018, 1910112963, 252163429,
42205629, 2914219, 454002, 127605, 231542, 110938, 15631, 44510, 13605, 23155,
3582, 12246, 12637, 1509, 296, 11112, 111290, 131172, 1127117, 76613, 9470,
13161, 21328, 11111114, 14142115,
3625334, 1125035, 348169, 78151, 11369, 1373, 220, 1135, 349, 70, 134, 119, 47,
15, 23, 9, 22, 15 CYCLE
->départ(9) : 9, 22, 15, 23, 9
CYCLE
->départ(10) : 10, 13, 6, 12, 112, 11114, 1733, 270,
12223, 7128, 11122225, 33991010, 13, 913661, 2107998, 12222775, 33910130,
131212367, 56113213, 6837229, 4201627, 266366, 112430, 131359, 7981, 969, 278,
134, 119, 47, 15, 23,
9, 22, 15 CYCLE
->départ(666) : 666, 12212, 111420, 11223114, 12423409,
814060, 11361126, 12489114, 12517098, 12517139, 1837214, 137769, 28359, 22933,
7820, 11379, 2527, 488, 11118, 12729, 2582, 1210, 1355, 358, 141, 215, 314,
137, 33, 25, 33 CYCLE
->départ(1000) : 1000, 111333, 271217, 23744,
111111416, 111668035, 38123416, 111333214, 111134771, 52041017, 4504142 1193600
11111113374, 1291293111, 210659941, 11635952, 111158582, 112114318, 13341506,
1455641 512354, 182534, 151042, 17438, 11087, 1344, 11111124, 11285010,
122351376, 11112431073, 272684284, 117283810, 134146302, 121044136, 1118132200,
111331051208, 111654243638, 14366699733, 2225493779, 81368636, 112001924,
112921719, 25911084, 112331838 128221488, 111122262170, 13566196845,
222320108177, 8863086101, 405548474, 116871062, 145241063, 5289904, 111182002, 14821986,
12181067, 902891, 522175, 332349, 234139, 20756, 11691, 22284, 1122114,
1242932, 1126858, 1141559, 95098, 17407, 6627, 21515, 3667, 844, 1147, 1112,
11134, 1862, 1448, 11142, 122114, 16152, 1112122, 155186, 111368, 1111646,
145756, 116409, 24089, 6729, 2334, 1277, 206, 127, 31, 11, 5, 3, 2, 1 STOP
Une belle illustration de Jean-Marc Falcoz
(« Je t'envoie le graphe des entiers jusqu'à 13 ; c'est 8 qui a la
plus longue trajectoire avant de boucler. »
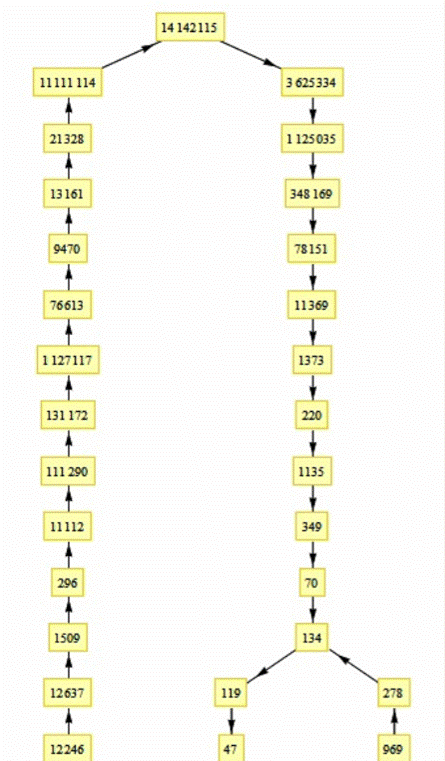
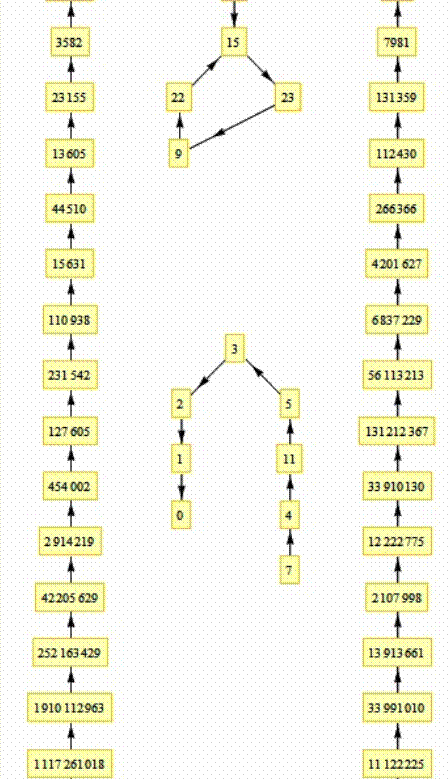
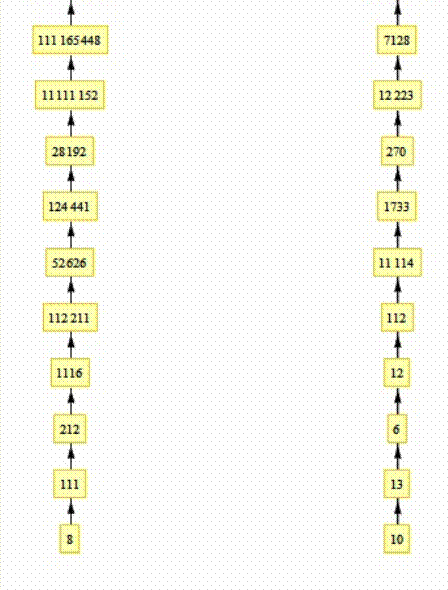
Il semble que tout finisse soit par 1, soit
dans une boucle (la boucle la plus courte est formée par 14 --> 2.7 =
"14" car les rangs des nombres premiers 2 et 7 sont 1 et 4).
Voici un dessin
grossier des sauts occasionnés par 57 (échelle logarithmique), lequel retombe
sur 1 en 102 étapes après avoir atteint un maximum de 222 312 455 509 au 32e
saut :
->départ(57) : 57, 28, 114, 128, 1111111, 52628,
111748, 114663, 212174, 110111, 35131, 81414, 122615, 33341, 4584, 111243,
25475, 33171, 21339, 22351, 41127, 21621, 2920, 111321, 2224811, 223249, 66216,
11121124, 11433636, 112222222214, 12728585125, 33310151505, 222312455509, 8862793537, 635356125,
2233346429, 114257278, 114102049, 8413199, 268133, 23498, 11175, 23335, 3672,
1112227, 56579, 10297, 4233, 2723, 477, 2216, 11159, 1351, 444, 11212, 11409,
2529, 2260, 11330, 13527, 222239, 111928, 1117143, 2281534, 141831, 2222727,
265781, 23292, 1122118, 146162, 128124, 1122499, 414712, 1115304, 11124803,
426181, 428104, 11117155, 3443261, 99961, 9589, 1448, 11142, 122114, 16152,
1112122, 155186, 111368, 1111646, 145756, 116409, 24089, 6729, 2334, 1277, 206,
127, 31, 11, 5, 3, 2, 1 :
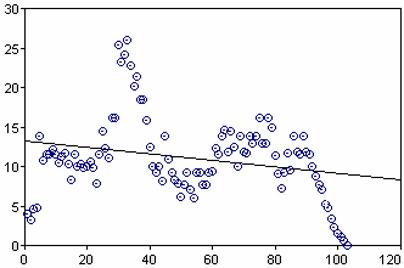
Cette idée est à l’origine d’un grand
nombre de suites qui sont entrées dans l’OEIS
de Neil Sloane :
-> A087712, par
exemple, se contente d’indiquer ce que devient un nombre « n » après
la première étape :
« a(1) = 1;
if n = kth prime, a(n) = k;
otherwise write all prime factors of n in nondecreasing order, replace each prime by its rank, and concatenate
the ranks. »
-> A098282 indique
la quantité d’étapes que produit « n » avant d’entrer dans une
boucle, « n » valant 1, puis 2, puis 3, etc.
« Iterate
the map k -> A087712(k) starting at n; a(n) is the number of steps at which
we see a repeated term for the first time;
or -1 if the trajectory never
repeats. »
-> A077960 montre
les étapes par lesquelles passe n = 18 avant de s’effondrer sur la valeur 1 (à
l’étape 111 ; l’ensemble des valeurs atteintes par n = 18 est ici, et son
diagramme ci-dessous) :
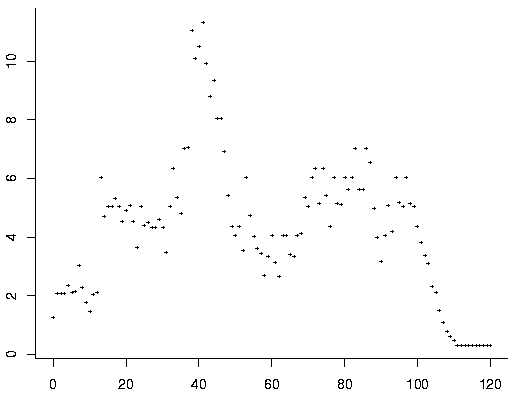
-> A145077 montre
la succession des valeurs maxima atteintes pour n=1, puis par n=2, n=3, etc.
(pour n=18 on voit ci-dessus que le maxima est atteint à l’étape 42 — avec la
cote 222312455509, échelle logarithmique toujours)
-> A145078 indique
la valeur minimale du plus petit entier faisant partie de la boucle dans
laquelle entre « n »
-> A145079 montre
la taille du cycle dans lequel entre n=1, puis n=2, n=3, etc.
-> A156055 est due
à Robert G. Wilson, membre de la
liste SeqFans
(sur laquelle, fort des résultats de Georges
Brougnard, j’avais répercuté l’idée) ; Robert a calculé le nombre d’étapes
nécessaires pour que « n » entre dans un cycle (il adopte la
convention que pour l’entier 1 le cycle vaut 1 — voir cependant la remarque de Farideh Firoozbakht
après le tableau en deux colonnes, 30 lignes plus bas) :
Number (i)
of iterations to repeat a term (starting with n):
i = 1,2,3,6,4,30,7,54,3,32, 5,29,31, 0,
3,19, 8,112,55,15,27, 3, 3,26, 1,20,223,102,33,13, 6,162, 1, 9,10,75,30,113,21,
...
n = 1 2 3 4
5 6 7
8 9 10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29 30 31
32 33 34 35 36 37 38 39 ...
On voit qu’il faut 30 étapes
à n=6 pour entrer dans un cycle (ou
s’effondrer sur 1) et aucune étape pour que 14 se reproduise à l’identique (en effet
14 se décompose en ses facteurs premiers 2.7, lesquels sont respectivement le 1er
et le 4e nombre premier => 14)
Qui calculera la suite S des plus petits entiers qui cyclent
en n étapes ?
Cette suite commence ainsi
(au vu des résultats de Robert G. Wilson,
ci-dessus) :
S = 14, 1, 2, 3,
5, 11, 4, 7, 17, 34, 35, ...
n =
0 1 2
3 4 5
6 7 8
9 10 ...
-> A144760 montre
la trajectoire de n=6
-> A144813 montre
la trajectoire de n=8
-> A144814 montre
la trajectoire de n=10
-> A144915 montre
la trajectoire de n=16
-> A144914 montre
le début de la trajectoire de n=40 (« Does this trajectory converge? »)
__________
Note du 11 février
2009 :
Suite à la remarque publiée
ce jour sur SeqFans
par Farideh Firoozbakht,
il semble qu’il faille réviser la façon de voir de Robert G. Wilson et retoucher sa suite A156055 :
Date: Wed,
11 Feb 2009 02:56:36 -0800 (PST)
From: Farideh Firoozbakht <mymontain(AT)yahoo.com>
Comments on A098282
Out of the first 1000 natural numbers there are only the following 62 numbers for which Mma [Mathematica]
can't compute a(n).
A={40,52,87,106,116,164,173,189,192,204,210,239,240,259,276,284,342,345,372,375,377,385,392,412,436,449,480,501,519,560,577,610,622,641,642,644,675,682,684,728,734,737,759,764,801,816,831,834,854,861,874,905,908,922,925,940,958,966,971,975,985,990}
For the remaining
n the values of {n,a(n)}
are:
n a(n)
|
1 |
1 |
|
2 |
2 |
|
3 |
3 |
|
4 |
6 |
|
5 |
4 |
|
6 |
31 |
|
7 |
7 |
|
8 |
55 |
|
9 |
4 |
|
10 |
33 |
|
11 |
5 |
|
12 |
30 |
|
13 |
32 |
|
14 |
1 |
|
15 |
4 |
|
16 |
19 |
|
17 |
8 |
|
18 |
112 |
|
19 |
56 |
|
20 |
16 |
|
21 |
27 |
|
22 |
4 |
|
23 |
4 |
|
24 |
26 |
|
25 |
2 |
|
26 |
20 |
|
27 |
223 |
|
28 |
102 |
|
29 |
34 |
|
30 |
14 |
|
31 |
6 |
|
32 |
162 |
|
33 |
2 |
|
34 |
9 |
|
35 |
10 |
|
36 |
75 |
|
37 |
31 |
|
38 |
113 |
|
39 |
21 |
|
41 |
33 |
|
42 |
20 |
|
43 |
2 |
|
44 |
23 |
|
45 |
30 |
|
46 |
57 |
|
47 |
5 |
|
48 |
28 |
|
49 |
24 |
|
50 |
30 |
|
51 |
224 |
|
53 |
20 |
|
54 |
295 |
|
55 |
11 |
|
56 |
85 |
|
57 |
103 |
|
58 |
140 |
|
59 |
9 |
|
60 |
71 |
|
61 |
113 |
|
62 |
55 |
|
63 |
34 |
|
64 |
110 |
|
65 |
76 |
|
66 |
49 |
|
67 |
57 |
|
68 |
110 |
|
69 |
35 |
|
70 |
8 |
|
71 |
17 |
|
72 |
165 |
|
73 |
28 |
|
74 |
30 |
|
75 |
226 |
|
76 |
111 |
|
77 |
31 |
|
78 |
153 |
|
79 |
5 |
|
80 |
77 |
|
81 |
112 |
|
82 |
16 |
|
83 |
5 |
|
84 |
144 |
|
85 |
32 |
|
86 |
102 |
|
88 |
69 |
|
89 |
27 |
|
90 |
277 |
|
91 |
58 |
|
92 |
7 |
|
93 |
7 |
|
94 |
23 |
|
95 |
114 |
|
96 |
62 |
|
97 |
3 |
|
98 |
99 |
|
99 |
94 |
|
100 |
115 |
|
101 |
21 |
|
102 |
8 |
|
103 |
224 |
|
104 |
53 |
|
105 |
28 |
|
107 |
103 |
|
108 |
23 |
|
109 |
35 |
|
110 |
139 |
|
111 |
54 |
|
112 |
29 |
|
113 |
15 |
|
114 |
101 |
|
115 |
22 |
|
117 |
109 |
|
118 |
110 |
|
119 |
6 |
|
120 |
11 |
|
121 |
12 |
|
122 |
111 |
|
123 |
13 |
|
124 |
19 |
|
125 |
48 |
|
126 |
152 |
|
127 |
7 |
|
128 |
100 |
|
129 |
102 |
|
130 |
107 |
|
131 |
163 |
|
132 |
182 |
|
133 |
29 |
|
134 |
7 |
|
135 |
138 |
|
136 |
106 |
|
137 |
3 |
|
138 |
103 |
|
139 |
10 |
|
140 |
163 |
|
141 |
6 |
|
142 |
12 |
|
143 |
86 |
|
144 |
98 |
|
145 |
35 |
|
146 |
13 |
|
147 |
77 |
|
148 |
26 |
|
149 |
11 |
|
150 |
94 |
|
151 |
76 |
|
152 |
76 |
|
153 |
26 |
|
154 |
36 |
|
155 |
112 |
|
156 |
16 |
|
157 |
32 |
|
158 |
112 |
|
159 |
111 |
|
160 |
220 |
|
161 |
25 |
|
162 |
24 |
|
163 |
114 |
|
165 |
112 |
|
166 |
14 |
|
167 |
22 |
|
168 |
361 |
|
169 |
50 |
|
170 |
4 |
|
171 |
157 |
|
172 |
85 |
|
174 |
10 |
|
175 |
12 |
|
176 |
175 |
|
177 |
228 |
|
178 |
20 |
|
179 |
34 |
|
180 |
75 |
|
181 |
21 |
|
182 |
14 |
|
183 |
104 |
|
184 |
32 |
|
185 |
13 |
|
186 |
92 |
|
187 |
104 |
|
188 |
69 |
|
190 |
104 |
|
191 |
3 |
|
193 |
24 |
|
194 |
49 |
|
195 |
107 |
|
196 |
64 |
|
197 |
31 |
|
198 |
38 |
|
199 |
58 |
|
200 |
275 |
|
201 |
60 |
|
202 |
153 |
|
203 |
116 |
|
205 |
78 |
|
206 |
8 |
|
207 |
32 |
|
208 |
78 |
|
209 |
141 |
|
211 |
6 |
|
212 |
53 |
|
213 |
12 |
|
214 |
101 |
|
215 |
5 |
|
216 |
110 |
|
217 |
227 |
|
218 |
103 |
|
219 |
59 |
|
220 |
11 |
|
221 |
58 |
|
222 |
222 |
|
223 |
29 |
|
224 |
33 |
|
225 |
93 |
|
226 |
108 |
|
227 |
25 |
|
228 |
156 |
|
229 |
31 |
|
230 |
11 |
|
231 |
31 |
|
232 |
21 |
|
233 |
225 |
|
234 |
27 |
|
235 |
111 |
|
236 |
106 |
|
237 |
223 |
|
238 |
78 |
|
241 |
21 |
|
242 |
113 |
|
243 |
144 |
|
244 |
76 |
|
245 |
30 |
|
246 |
40 |
|
247 |
111 |
|
248 |
162 |
|
249 |
30 |
|
250 |
86 |
|
251 |
296 |
|
252 |
88 |
|
253 |
10 |
|
254 |
164 |
|
255 |
224 |
|
256 |
173 |
|
257 |
12 |
|
258 |
20 |
|
260 |
72 |
|
261 |
62 |
|
262 |
183 |
|
263 |
86 |
|
264 |
131 |
|
265 |
76 |
|
266 |
27 |
|
267 |
34 |
|
268 |
32 |
|
269 |
104 |
|
270 |
26 |
|
271 |
141 |
|
272 |
33 |
|
273 |
41 |
|
274 |
30 |
|
275 |
121 |
|
277 |
10 |
|
278 |
8 |
|
279 |
217 |
|
280 |
25 |
|
281 |
72 |
|
282 |
32 |
|
283 |
114 |
|
285 |
79 |
|
286 |
17 |
|
287 |
30 |
|
288 |
98 |
|
289 |
32 |
|
290 |
139 |
|
291 |
94 |
|
292 |
126 |
|
293 |
56 |
|
294 |
56 |
|
295 |
51 |
|
296 |
28 |
|
297 |
115 |
|
298 |
139 |
|
299 |
36 |
|
300 |
129 |
|
301 |
63 |
|
302 |
107 |
|
303 |
109 |
|
304 |
13 |
|
305 |
39 |
|
306 |
27 |
|
307 |
35 |
|
308 |
76 |
|
309 |
26 |
|
310 |
34 |
|
311 |
111 |
|
312 |
12 |
|
313 |
77 |
|
314 |
4 |
|
315 |
110 |
|
316 |
75 |
|
317 |
50 |
|
318 |
38 |
|
319 |
119 |
|
320 |
67 |
|
321 |
157 |
|
322 |
12 |
|
323 |
154 |
|
324 |
117 |
|
325 |
49 |
|
326 |
104 |
|
327 |
32 |
|
328 |
77 |
|
329 |
156 |
|
330 |
36 |
|
331 |
58 |
|
332 |
71 |
|
333 |
47 |
|
334 |
11 |
|
335 |
120 |
|
336 |
48 |
|
337 |
111 |
|
338 |
15 |
|
339 |
12 |
|
340 |
123 |
|
341 |
19 |
|
343 |
51 |
|
344 |
29 |
|
346 |
164 |
|
347 |
36 |
|
348 |
67 |
|
349 |
9 |
|
350 |
74 |
|
351 |
130 |
|
352 |
266 |
|
353 |
18 |
|
354 |
60 |
|
355 |
68 |
|
356 |
144 |
|
357 |
112 |
|
358 |
7 |
|
359 |
166 |
|
360 |
86 |
|
361 |
70 |
|
362 |
13 |
|
363 |
225 |
|
364 |
232 |
|
365 |
158 |
|
366 |
274 |
|
367 |
29 |
|
368 |
34 |
|
369 |
38 |
|
370 |
68 |
|
371 |
151 |
|
373 |
31 |
|
374 |
33 |
|
376 |
175 |
|
378 |
292 |
|
379 |
227 |
|
380 |
52 |
|
381 |
32 |
|
382 |
87 |
|
383 |
112 |
|
384 |
91 |
|
386 |
99 |
|
387 |
232 |
|
388 |
182 |
|
389 |
32 |
|
390 |
18 |
|
391 |
6 |
|
393 |
22 |
|
394 |
36 |
|
395 |
13 |
|
396 |
54 |
|
397 |
154 |
|
398 |
14 |
|
399 |
163 |
|
400 |
24 |
|
401 |
6 |
|
402 |
26 |
|
403 |
183 |
|
404 |
16 |
|
405 |
159 |
|
406 |
130 |
|
407 |
125 |
|
408 |
22 |
|
409 |
78 |
|
410 |
115 |
|
411 |
226 |
|
413 |
29 |
|
414 |
62 |
|
415 |
155 |
|
416 |
150 |
|
417 |
28 |
|
418 |
113 |
|
419 |
113 |
|
420 |
206 |
|
421 |
17 |
|
422 |
78 |
|
423 |
101 |
|
424 |
78 |
|
425 |
112 |
|
426 |
461 |
|
427 |
114 |
|
428 |
156 |
|
429 |
174 |
|
430 |
40 |
|
431 |
6 |
|
432 |
219 |
|
433 |
145 |
|
434 |
13 |
|
435 |
247 |
|
437 |
28 |
|
438 |
129 |
|
439 |
33 |
|
440 |
90 |
|
441 |
107 |
|
442 |
23 |
|
443 |
103 |
|
444 |
50 |
|
445 |
118 |
|
446 |
27 |
|
447 |
112 |
|
448 |
127 |
|
450 |
24 |
|
451 |
254 |
|
452 |
35 |
|
453 |
107 |
|
454 |
12 |
|
455 |
165 |
|
456 |
231 |
|
457 |
70 |
|
458 |
95 |
|
459 |
74 |
|
460 |
103 |
|
461 |
28 |
|
462 |
108 |
|
463 |
278 |
|
464 |
265 |
|
465 |
31 |
|
466 |
77 |
|
467 |
59 |
|
468 |
221 |
|
469 |
114 |
|
470 |
146 |
|
471 |
224 |
|
472 |
33 |
|
473 |
114 |
|
474 |
295 |
|
475 |
16 |
|
476 |
27 |
|
477 |
54 |
|
478 |
77 |
|
479 |
8 |
|
481 |
18 |
|
482 |
27 |
|
483 |
31 |
|
484 |
224 |
|
485 |
50 |
|
486 |
122 |
|
487 |
8 |
|
488 |
13 |
|
489 |
79 |
|
490 |
75 |
|
491 |
24 |
|
492 |
223 |
|
493 |
184 |
|
494 |
362 |
|
495 |
9 |
|
496 |
110 |
|
497 |
207 |
|
498 |
277 |
|
499 |
115 |
|
500 |
205 |
|
502 |
37 |
|
503 |
63 |
|
504 |
147 |
|
505 |
105 |
|
506 |
112 |
|
507 |
28 |
|
508 |
111 |
|
509 |
4 |
|
510 |
118 |
|
511 |
18 |
|
512 |
124 |
|
513 |
253 |
|
514 |
113 |
|
515 |
33 |
|
516 |
245 |
|
517 |
34 |
|
518 |
27 |
|
520 |
153 |
|
521 |
100 |
|
522 |
197 |
|
523 |
95 |
|
524 |
34 |
|
525 |
11 |
|
526 |
17 |
|
527 |
113 |
|
528 |
127 |
|
529 |
95 |
|
530 |
229 |
|
531 |
160 |
|
532 |
117 |
|
533 |
31 |
|
534 |
152 |
|
535 |
78 |
|
536 |
34 |
|
537 |
22 |
|
538 |
33 |
|
539 |
119 |
|
540 |
44 |
|
541 |
116 |
|
542 |
113 |
|
543 |
114 |
|
544 |
164 |
|
545 |
157 |
|
546 |
50 |
|
547 |
22 |
|
548 |
115 |
|
549 |
81 |
|
550 |
214 |
|
551 |
77 |
|
552 |
38 |
|
553 |
79 |
|
554 |
112 |
|
555 |
11 |
|
556 |
163 |
|
557 |
9 |
|
558 |
226 |
|
559 |
116 |
|
561 |
13 |
|
562 |
221 |
|
563 |
225 |
|
564 |
72 |
|
565 |
37 |
|
566 |
26 |
|
567 |
63 |
|
568 |
57 |
|
569 |
54 |
|
570 |
86 |
|
571 |
29 |
|
572 |
130 |
|
573 |
145 |
|
574 |
74 |
|
575 |
13 |
|
576 |
76 |
|
578 |
229 |
|
579 |
77 |
|
580 |
17 |
|
581 |
102 |
|
582 |
38 |
|
583 |
246 |
|
584 |
66 |
|
585 |
93 |
|
586 |
25 |
|
587 |
104 |
|
588 |
134 |
|
589 |
8 |
|
590 |
81 |
|
591 |
31 |
|
592 |
62 |
|
593 |
24 |
|
594 |
458 |
|
595 |
37 |
|
596 |
11 |
|
597 |
41 |
|
598 |
51 |
|
599 |
36 |
|
600 |
149 |
|
601 |
140 |
|
602 |
112 |
|
603 |
79 |
|
604 |
72 |
|
605 |
69 |
|
606 |
27 |
|
607 |
55 |
|
608 |
265 |
|
609 |
37 |
|
611 |
182 |
|
612 |
17 |
|
613 |
30 |
|
614 |
115 |
|
615 |
181 |
|
616 |
31 |
|
617 |
16 |
|
618 |
27 |
|
619 |
102 |
|
620 |
62 |
|
621 |
39 |
|
623 |
79 |
|
624 |
209 |
|
625 |
56 |
|
626 |
113 |
|
627 |
21 |
|
628 |
123 |
|
629 |
362 |
|
630 |
170 |
|
631 |
23 |
|
632 |
165 |
|
633 |
112 |
|
634 |
15 |
|
635 |
59 |
|
636 |
158 |
|
637 |
28 |
|
638 |
61 |
|
639 |
359 |
|
640 |
86 |
|
643 |
110 |
|
645 |
51 |
|
646 |
21 |
|
647 |
111 |
|
648 |
137 |
|
649 |
35 |
|
650 |
60 |
|
651 |
9 |
|
652 |
52 |
|
653 |
7 |
|
654 |
62 |
|
655 |
72 |
|
656 |
220 |
|
657 |
60 |
|
658 |
72 |
|
659 |
12 |
|
660 |
147 |
|
661 |
13 |
|
662 |
23 |
|
663 |
35 |
|
664 |
11 |
|
665 |
68 |
|
666 |
30 |
|
667 |
77 |
|
668 |
103 |
|
669 |
163 |
|
670 |
7 |
|
671 |
28 |
|
672 |
247 |
|
673 |
112 |
|
674 |
362 |
|
676 |
114 |
|
677 |
14 |
|
678 |
130 |
|
679 |
113 |
|
680 |
316 |
|
681 |
31 |
|
683 |
20 |
|
685 |
48 |
|
686 |
160 |
|
687 |
87 |
|
688 |
33 |
|
689 |
32 |
|
690 |
169 |
|
691 |
49 |
|
692 |
82 |
|
693 |
234 |
|
694 |
51 |
|
695 |
12 |
|
696 |
105 |
|
697 |
19 |
|
698 |
5 |
|
699 |
297 |
|
700 |
100 |
|
701 |
153 |
|
702 |
94 |
|
703 |
84 |
|
704 |
136 |
|
705 |
20 |
|
706 |
158 |
|
707 |
462 |
|
708 |
235 |
|
709 |
8 |
|
710 |
183 |
|
711 |
112 |
|
712 |
361 |
|
713 |
18 |
|
714 |
4 |
|
715 |
145 |
|
716 |
131 |
|
717 |
89 |
|
718 |
86 |
|
719 |
101 |
|
720 |
206 |
|
721 |
115 |
|
722 |
70 |
|
723 |
11 |
|
724 |
32 |
|
725 |
62 |
|
726 |
62 |
|
727 |
103 |
|
729 |
205 |
|
730 |
112 |
|
731 |
5 |
|
732 |
72 |
|
733 |
108 |
|
735 |
110 |
|
736 |
22 |
|
738 |
160 |
|
739 |
164 |
|
740 |
113 |
|
741 |
33 |
|
742 |
211 |
|
743 |
183 |
|
744 |
157 |
|
745 |
121 |
|
746 |
11 |
|
747 |
138 |
|
748 |
211 |
|
749 |
157 |
|
750 |
156 |
|
751 |
30 |
|
752 |
266 |
|
753 |
165 |
|
754 |
90 |
|
755 |
49 |
|
756 |
145 |
|
757 |
8 |
|
758 |
13 |
|
760 |
41 |
|
761 |
139 |
|
762 |
155 |
|
763 |
175 |
|
765 |
73 |
|
766 |
176 |
|
767 |
17 |
|
768 |
58 |
|
769 |
107 |
|
770 |
114 |
|
771 |
225 |
|
772 |
64 |
|
773 |
4 |
|
774 |
32 |
|
775 |
74 |
|
776 |
131 |
|
777 |
149 |
|
778 |
229 |
|
779 |
22 |
|
780 |
359 |
|
781 |
154 |
|
782 |
35 |
|
783 |
90 |
|
784 |
316 |
|
785 |
112 |
|
786 |
190 |
|
787 |
104 |
|
788 |
76 |
|
789 |
174 |
|
790 |
127 |
|
791 |
41 |
|
792 |
100 |
|
793 |
28 |
|
794 |
21 |
|
795 |
135 |
|
796 |
232 |
|
797 |
11 |
|
798 |
158 |
|
799 |
146 |
|
800 |
74 |
|
802 |
35 |
|
803 |
101 |
|
804 |
33 |
|
805 |
10 |
|
806 |
161 |
|
807 |
13 |
|
808 |
12 |
|
809 |
164 |
|
810 |
76 |
|
811 |
7 |
|
812 |
83 |
|
813 |
21 |
|
814 |
123 |
|
815 |
16 |
|
817 |
124 |
|
818 |
76 |
|
819 |
160 |
|
820 |
87 |
|
821 |
13 |
|
822 |
94 |
|
823 |
87 |
|
824 |
22 |
|
825 |
8 |
|
826 |
364 |
|
827 |
99 |
|
828 |
185 |
|
829 |
36 |
|
830 |
179 |
|
832 |
125 |
|
833 |
113 |
|
835 |
13 |
|
836 |
57 |
|
837 |
182 |
|
838 |
22 |
|
839 |
14 |
|
840 |
231 |
|
841 |
27 |
|
842 |
15 |
|
843 |
73 |
|
844 |
27 |
|
845 |
275 |
|
846 |
225 |
|
847 |
166 |
|
848 |
150 |
|
849 |
63 |
|
850 |
105 |
|
851 |
68 |
|
852 |
80 |
|
853 |
78 |
|
855 |
112 |
|
856 |
231 |
|
857 |
27 |
|
858 |
317 |
|
859 |
12 |
|
860 |
71 |
|
862 |
105 |
|
863 |
95 |
|
864 |
238 |
|
865 |
124 |
|
866 |
33 |
|
867 |
11 |
|
868 |
172 |
|
869 |
198 |
|
870 |
259 |
|
871 |
103 |
|
872 |
38 |
|
873 |
115 |
|
875 |
71 |
|
876 |
238 |
|
877 |
77 |
|
878 |
14 |
|
879 |
184 |
|
880 |
237 |
|
881 |
77 |
|
882 |
119 |
|
883 |
27 |
|
884 |
12 |
|
885 |
61 |
|
886 |
93 |
|
887 |
37 |
|
888 |
242 |
|
889 |
7 |
|
890 |
13 |
|
891 |
68 |
|
892 |
117 |
|
893 |
17 |
|
894 |
36 |
|
895 |
20 |
|
896 |
20 |
|
897 |
105 |
|
898 |
105 |
|
899 |
34 |
|
900 |
33 |
|
901 |
132 |
|
902 |
34 |
|
903 |
104 |
|
904 |
112 |
|
906 |
18 |
|
907 |
113 |
|
909 |
130 |
|
910 |
76 |
|
911 |
17 |
|
912 |
67 |
|
913 |
96 |
|
914 |
70 |
|
915 |
96 |
|
916 |
24 |
|
917 |
220 |
|
918 |
59 |
|
919 |
33 |
|
920 |
59 |
|
921 |
87 |
|
923 |
63 |
|
924 |
140 |
|
926 |
105 |
|
927 |
74 |
|
928 |
195 |
|
929 |
113 |
|
930 |
26 |
|
931 |
128 |
|
932 |
106 |
|
933 |
132 |
|
934 |
4 |
|
935 |
113 |
|
936 |
171 |
|
937 |
112 |
|
938 |
76 |
|
939 |
77 |
|
941 |
221 |
|
942 |
118 |
|
943 |
97 |
|
944 |
164 |
|
945 |
220 |
|
946 |
164 |
|
947 |
26 |
|
948 |
23 |
|
949 |
40 |
|
950 |
159 |
|
951 |
28 |
|
952 |
178 |
|
953 |
25 |
|
954 |
16 |
|
955 |
52 |
|
956 |
90 |
|
957 |
73 |
|
959 |
146 |
|
960 |
56 |
|
961 |
19 |
|
962 |
228 |
|
963 |
253 |
|
964 |
5 |
|
965 |
30 |
|
967 |
115 |
|
968 |
146 |
|
969 |
9 |
|
970 |
33 |
|
972 |
139 |
|
973 |
14 |
|
974 |
25 |
|
976 |
265 |
|
977 |
113 |
|
978 |
86 |
|
979 |
35 |
|
980 |
247 |
|
981 |
39 |
|
982 |
50 |
|
983 |
15 |
|
984 |
260 |
|
986 |
162 |
|
987 |
103 |
|
988 |
32 |
|
989 |
71 |
|
991 |
23 |
|
992 |
100 |
|
993 |
35 |
|
994 |
28 |
|
995 |
165 |
|
996 |
75 |
|
997 |
362 |
|
998 |
108 |
|
999 |
122 |
|
1000 |
99 |
It's interesting that a(222)=222.
The known
fixed points of A098282 (a(n)=n) are: 1, 2, 3, 7,
222, ...
Presumably if n is in A then a(n)<>n.
Farideh
Le programme Mathematica
utilisé par Farideh
réécrirait alors la suite A156055 de Robert G. Wilson ainsi (les
désaccords sont soulignés) :
Number (i)
of iterations to repeat a term (starting with n):
i = 1,2,3,6,4,31,7,55,4,33,
5,30,32, 1, 4,19, 8,112,56,16,27, 4,
4,26, 2,20,223,102,34,14, 6,162, 2, 9,10,75,31,113,21,
...
n = 1 2 3 4
5 6 7
8 9 10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29 30 31
32 33 34 35 36 37 38 39 ...
Le programme GBnums de Georges Brougnard,
indépendamment de Mathematica,
valide toutes les valeurs de Farideh.
__________
La plupart de ces calculs
peuvent être vérifiés à la main en utilisant ces tables :
- liste des cent mille premiers nombres premiers
(par Neil Sloane) :
http://www.research.att.com/~njas/sequences/a000040.txt
>
- liste des nombres premiers
allant de un (1) à mille milliards
(1012), mais fonctionnant par « fenêtres » ; le curseur
de la souris, glissé sur un nombre composé, en affiche immédiatement la
décomposition en facteurs) :
http://www.walter-fendt.de/m14f/primes_f.htm
__________
Note supplémentaire :
Il est intéressant de
remarquer qu’on peut travailler à
l’envers, et calculer facilement le ou les prédécesseurs
d’un nombre.
a) Les nombres u de 1 à 9 n’ont qu’un seul prédécesseur : c’est le ue premier (ainsi 5 n’a-t-il
que 11 comme prédécesseur car 11, n’étant pas décomposable doit être remplacé
par 5 — comme nous l’avons vu plus haut dans la remarque ; 11 est en effet le 5e premier)
b) les nombres composés d’un
chiffre unique suivi d’un ou plusieurs zéros n’ont qu’un prédécesseur également
(10, par exemple, ou 200, ne peuvent provenir que de 29 ou 1223, respectivement
10e et 200e nombre premier).
c) presque tous les autres
nombres sont susceptibles d’avoir plusieurs prédécesseurs : 1234, par
exemple pourrait venir de (noter l’inversion de la flèche et du sens de
lecture) :
1234 <- 1.234 <= 2 x
1481 = "2962"
1234 <- 12.34 <= 37 x
139 = "5143"
1234 <- "1234"
<- "10061" (car 10061 est le 1234e premier)
On remarquera qu’il manque
une ligne ci-dessus :
1234 <- 123.4 <= 677 x
7 = "4739".
Cette ligne est absente car
on ne peut présenter les facteurs de "4739" du plus grand (677) au
plus petit (7). La procédure normale oblige à décomposer "4739" en 7
x 677, ce qui produit 4.123 puis "4123" après concaténation. Ce n’est
pas la même chose que "1234"... Il faut donc être prudent quand on
calcule les prédécesseurs [on verra ci-dessous que certains nombres échappant
aux catégories (a) et (b) plus haut n’ont qu’un prédécesseur].
Petit tableau (à compléter par une âme
charitable...) des prédécesseurs successifs de n :
préd(-1) préd(-2)
n de n de n
1
2 3
2
3 5
3
5 7
4
7 11
5
11 31,
4
6
13 41, 10
7
17 59, 34
8
19 67, 46
9
23 83, 15
10 29
109, 69
11 31,
4 127, 7
12 37,
6 157, 85, 13
13 41,
10 179, 29
14 43, 14 191,
43, 14
15 47,
22 211, 119, 79, 9
16 53,
26 241, 101, 39
17 59,
34 277, 253, 139, 35
18 61,
38 283, 163, 95
19 67,
46 ... etc.
20 71
21 73
22 79,
9
23 83,
15
24 89,
21
25 97,
33
26 101,
39
27 103,
51
28 107,
57
29 109,
69
30 113
31 127
32 131
33 137,
25
34 139,
35
35 149,
55
36 151,
65
37 157,
85
38 163,
95
39 167, 115
40 173
... etc.
__________
Retour à la page d’accueil
des amusettes maths, ici.
Retour tout court à
l’accueil, là.