______________________________________

51 + 11 – 6 = 101 + 15 – 60

______________________________________

(56 = 56) .

Outre sa vérité arithmétique, cette égalité présente la particularité que les trois nombres de gauche et les trois nombres de droite s’écrivent avec les mêmes lettres :

CINQUANTE ET UN + ONZE – SIX = CENT UN + QUINZE – SOIXANTE

On aurait pu également présenter cette anagramme ainsi :

CINQUANTEETUNPLUSONZEMOINSSIX

CENTUNPLUSQUINZEMOINSSOIXANTE

L’histoire de cette formule commence par une question récurrente sur la liste « Oulipo » :

> ELEVEN + TWO = TWELVE + ONE

> Qui trouvera un résultat équivalent en français ?

Tout avait démarré, semble-t-il, le 17 Novembre 1998 à 10:22:06 +0100 par un message de Nicolas Graner :

> Voici de superbes anagrammes anglaises que j’ai reçues de

> quelqu’un qui les a reçues de quelqu’un qui les a reçues

> d’un technicien de l’université de Leeds (UK). Je n’en sais

> pas plus sur leur origine :-)

> J’espère surtout que celle sur « eleven plus two » donnera

> des idées à nos anagrammologues francophones...

Nicolas

-------

> Dormitory = Dirty Room

> Evangelist = Evil’s Agent

> Desperation = A Rope Ends It

> The Morse Code = Here Come Dots

[...]

> Eleven plus two = Twelve plus one

-------

Quand ce sujet revint sur la liste, quelques années plus tard, Nicolas ajouta qu’il fallait évidemment exclure les « propositions triviales¹ du genre : vingt + TROIS = vingt-trois ».

Je pensais à tout cela, lundi dernier (17 mars 2003). Je me demandais pourquoi Nicolas avait pris l’exemple de 23 et pas de 22. Ou de 21. Je souris : VINGT ET UN, à l’évidence, ne convenait pas puisque distinct de VINGT + UN par le digramme ET... Puis j’eus une illumination : au fond, il y avait là une sorte d’« équation » permettant de remplacer le digramme ET par une expression « alphanumérique » simple :

(a) ET = 21 – 20 – 1

De même je savais, et nous savons tous, que QUATORZE « contient » QUATRE. Cela conduisait à une autre équation :

(b) OZ = 14 – 4

Idem pour QUARANTE, lequel englobe QUATRE, donc :

(c) AN = 40 – 4

Un début de table de digrammes « alphanumériques » se mettait en place. Si l’on pouvait écrire, à l’aide de lettres ainsi mises en évidence, un nombre non-utilisé encore dans les équations, l’affaire serait faite !

J’ai donc commencé une liste de nombres « élémentaires » qui en contiennent d’autres :

— NEUF contient UN (malheureusement NEUF contient aussi F, lequel F n’est présent dans aucun autre nombre élémentaire ; impossible à utiliser donc. Pareil pour HUIT qui contient un H unique. Et SEPT qui contient le seul P).

— QUINZE contient UN, ce qui conduit à l’équation :

(d) QIZE = 15 – 1

— QUARANTE contient QUATRE, on l’a vu, mais aussi UN :

(e) QARATE = 40 – 1

— CINQUANTE contient CINQ, UN et CENT :

(f) ATE = 50 – 5 – 1

(g) AQI = 50 – 100 – 1

— SOIXANTE contient SIX :

(h) OANTE = 60 – 6

Les autres nombres ne produisent rien. En revanche un examen approfondi des lettres que partagent certains d’entre eux permet de trouver des choses comme :

DIX + SEIZE + TR = TREIZE + SIX + D qui peut s’écrire :

(i) TR – D = 13 – 6 – 10 – 16

Ou comme :

ONZE + R = ZÉRO + N soit :

(j) R – N = 0 – 11

Ou encore :

DOUZE + X = DEUX + ZO soit :

(k) X – ZO = 12 - 2

etc.

On parvient assez vite à isoler des lettres individuelles. Par exemple en faisant (f) – (a) on trouve (k) :

(f) ATE = 50 – 5 – 1

(a) ET = 21 – 20 – 1

--- -----------

(k) A = 50 – 5 – 1 – 21 + 20 + 1

= 50 – 5 – 21 + 20

De même en faisant (h) – (a) - (c) on trouve (m) :

(h) OANTE = 60 – 6

----- ------

(a) ET = 21 – 20 – 1

(c) AN = 40 – 4

(m) O = 60 – 6 – 21 + 20 + 1 – 40 + 4

En faisant (b) + (k) on trouve (n) :

(b) OZ = 14 – 4

(k) X – ZO = 12 – 2

------ ------

(n) X = 14 + 12 – 4 – 2

De proche en proche, et en veillant toujours à ne pas tourner en rond avec les équations, on finira par trouver des solutions du type de celle qui ouvre cette page...

Attention, exhiber deux groupes de nombres anagrammes l’un de l’autre ne suffit pas ! Il faut encore les combiner subtilement à l’aide de signes plus et moins pour que les comptes arithmétiques tournent...

__________

Voici, par exemple, et tous tâtonnements disparus, la marche suivie pour trouver le résultat plus haut :

QUINZE + O = ONZE + QUI

[ajout de CENT] :

CENT + 15 + O = 11 + QUI + CENT

[ajout de AN] :

100 + 15 + O + AN = 11 + QUI + CENT + AN

[mélange] :

100 + 15 + O + AN = 11 + CINQUANTE

[ajout de QUATRE] :

100 + 15 + O + AN + QUATRE = 11 + 50 + QUATRE

[mélange] :

100 + 15 + O + QUARANTE = 11 + 50 + 4

[utilisation de l’équation (m) pour O] :

100 + 15 + [60 – 6 – 21 + 20 + 1 – 40 + 4] + 40 = 11 + 50 + 4

[suppression des crochets et simplification des termes soulignés] :

100 + 15 + 60 – 6 – 21 + 20 + 1 = 11 + 50

[passage des nombres négatifs de l’autre côté du signe égale] :

100 + 15 + 60 + 20 + 1 = 6 + 21 + 11 + 50

[transformation (à droite) de 21 + 50 en 20 + 51 et simplification des termes soulignés] :

100 + 15 + 60 + 1 = 6 + 11 + 51

[compactage et nouvel ordre des termes] :

101 + 15 + 60 = 51 + 11 + 6

Muni de deux signes moins, c’est le résultat déjà signalé.

(La petite animation ci-dessous m’a été envoyée en juillet 2011 par Basile Morin, via la liste Oulipo – merci à lui !)

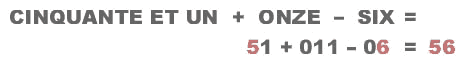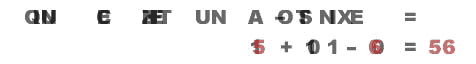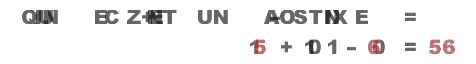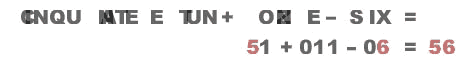
Je voulais, il y a quelques jours, trouver une formule qui ne comportât pas de signe moins, à l’instar de l’anglo-saxonne 11 + 2 = 12 + 1. Et qui satisfît aussi à un autre critère, surnommé « l’anagraal » par Nicolas Graner² : que les chiffres à gauche du signe « = » soient les mêmes qu’à droite — comme dans la formule 11 + 2 = 12 + 1 où l’on compte deux 1 et un 2 dans chaque membre de l’égalité : après l’anagramme de lettres, l’anagramme de chiffres ! (En plus de la vérité arithmétique).

La première difficulté fut d’obtenir des totaux identiques dans chaque membre sans employer de signe moins. L’écart à combler était de 108 — la partie gauche valant 176 et la droite 68. Comment faire ?

L’astuce consista à utiliser des nombres « composés » (par opposition aux nombres élémentaires rencontrés plus haut). En « dé-composant » de tels nombres on approche du but : 220 et 122 (DEUX, CENT, VINGT <——> CENT, VINGT, DEUX) par exemple, utilisent les mêmes mots et les mêmes lettres, pourtant leur différence vaut 98.

En combinant avec patience de tels nombres, on finit par trouver l’un des anagraals suivants (l’égalité d’origine est en jaune pâle) :

____________________________

2101 + 915 + 360 + 302 + 2

=

3051 + 211 + 206 + 203 + 9

____________________________

Cette expression satisfait donc aux six critères de l’anagraal granérien :

a) même total G/D (3680)

b) mêmes lettres G/D

c) mêmes chiffres G/D

d) même quantité de nombres G/D

e) uniquement des signes +

f) aucun nombre répété

... mais le résultat est nettement moins sexy que l’anglo-saxon « ELEVEN + TWO = TWELVE + ONE », c’est vrai !

Y a-t-il moyen de faire mieux, plus compact, plus élégant³ ? Who knows !

__________

[Note du 3 octobre 2008] :

À l’occasion d’un jeu lancé par Erich Friedman, Jean-Charles Meyrignac a trouvé (le 3 octobre 2008), que les lettres écrivant ces deux nombres sont les mêmes (en français) :

CINQUANTE-SIX MILLE SOIXANTE ET ONZE (56071) et

SOIXANTE MILLE CENT SOIXANTE-QUINZE (60175)

En supprimant MILLE en haut et en bas on dispose des unités lexicales suivantes pour résoudre notre problème :

CINQUANTE / SIX / SOIXANTE / ET / ONZE = SOIXANTE / CENT / SOIXANTE / QUINZE

En jouant avec les signes « plus » et « moins » de façon ad hoc, on finit par trouver :

SOIXANTE ET ONZE + CINQUANTE - SIX = CENT + SOIXANTE-QUINZE - SOIXANTE

71 + 50 - 6 = 100 + 75 - 60

... ce qui est vrai : 115 = 115

C’est donc là une seconde solution au problème cherché : bravo Jean-Charles ! (elle revient à remplacer le mot « UN » de la première solution par le mot « SOIXANTE » et à recombiner les termes ; le courriel complet de Jean-Charles à Erich est là)

______________________________________

71 + 50 – 6 = 100 + 75 – 60

______________________________________

(115 = 115)

Cette égalité, écrite comme suit, est une jolie anagramme de lettres et de chiffres (mais pas de signes) :

______________________________

71 + 50 - 6 = 175 - 60

______________________________

(115 = 115)

Pour que lettres, chiffres et signes soient identiques des deux côtés, il faut alourdir l’égalité en lui ajoutant CENT, CENT, UN de chaque côté et trois signes « + » en tout (en bleu) :

_________________________________________________________

101 + 71 + 50 – 106 = 175 – 160 + 100 + 1

_________________________________________________________

(116 = 116)

Peut-on faire mieux ?

Plus économe en signes typographiques ? Il y en a treize ici (hors espaces) de chaque côté du signe « = »

On aurait pu charger encore la barque en se proposant de pandigitaliser le binz (les chiffres de 0 à 9 sont tous représentés, une et une seule fois chacun, dans chaque membre). Le cœur inchangé de l’opération est en rouge ; plusieurs autres solutions sont possibles (par permutations des centaines, par disjonction des parties constitutives d’un nombre, etc.) :

_________________________________________________________

329 + 71 + 58 – 406 = 175 – 460 + 328 + 9

_________________________________________________________

(52 = 52)

__________

[Note du 7 octobre 2008] :

Jean-Charles Meyrignac a cherché (à l’aide d’un sien programme en langage C) tous les « noyaux anagrammes » pouvant donner des égalités du type ELEVEN + TWO = TWELVE + ONE en français. Le corpus de « mots-nombres » utilisé est :

ZERO, UN, DEUX, TROIS, QUATRE, CINQ, SIX, SEPT, HUIT, NEUF, DIX, ONZE, DOUZE, TREIZE, QUATORZE, QUINZE, SEIZE, VINGT, ET, VINGTS, TRENTE, QUARANTE, CINQUANTE, SOIXANTE, CENT, CENTS, MILLE, MILLION, MILLIONS, MILLIARD, MILLIARDS.

Le résultat est listé là.

Le « noyau anagramme » le plus court de cette liste permet ce petit quiz (paru ce jour sur fr.sci.maths et la liste Oulipo) :

Quiz : Quand cette égalité est-elle vraie ?

0 + 21000000 = 1 + 11023

Réponse : ... quand on l'écrit en toutes lettres :

ZEROPLUSVINGTETUNMILLIONS =

UNPLUSONZEMILLEVINGTTROIS

Jean-Charles n’aimant pas trop les signes « - » a cherché la plus petite égalité ne comportant que des « + ». Elle apparut à partir du noyau [ET DEUX TROIS QUINZE QUARANTE CENT <=> QUATRE SIX DOUZE TRENTE CINQUANTE]. Chaque côté du signe « = » vaut 781 :

__________________________________________________

345 + 221 + 215 = 592 + 156 + 32 + 1

__________________________________________________

(781 = 781)

Soit :

TROIS CENT QUARANTE-CINQ + DEUX CENT VINGT ET UN + DEUX CENT QUINZE = CINQ CENT QUATRE-VINGT-DOUZE + CENT CINQUANTE-SIX + TRENTE-DEUX + UN.

__________

[Note du 16 octobre 2008] :

L’égalité de Jean-Charles en jaune pâle ci-dessus est améliorable – il suffit par exemple d’augmenter la quantité de termes admis à gauche du signe « = » (le programme de Jean-Charles en fixe par défaut sept maximum à gauche et dix à droite : < #define MAX_LEFT 7 //#define MAX_RIGHT 10 >, comme on peut toujours le voir là).

On trouvera ici la table des nombres « composés » évoqués plus haut, laquelle permit de trouver à la main ce qui semble constituer l’anagraal minimal record (238) à l’heure actuelle :

_______________________________________________________________

2+5+14+16+25+41+61+74 = 4+6+11+12+24+54+56+71

_______________________________________________________________

(238 = 238)

__________

1. La plus petite de ces égalités triviales est 17+8=18+7 [DIX-SEPT + HUIT = DIX-HUIT + SEPT]. Mais que penser de 200+81=201+80 ? [DEUX CENTS + QUATRE-VINGT UN = DEUX CENT UN + QUATRE-VINGTS] ; ici un S se promène d’un mot à l’autre...

2. Merci à Nicolas Graner pour ses archives informatiques, ses encouragements et ses listes infinies de nombres bizarres !

3. En attendant, voici une manière de présenter le résultat ci-dessus qui vérifie un 5^e critère : le trouverez-vous ? (les quatre autres sont : égalité arithmétique, égalité de lettres, de chiffres, de signes). Solution sous le signe égale...

915 + 1 + 160 + 2300 + 2 + 302 = 203 + 200 + 3206 + 11 + 51 + 9

__________

L’égalité anagrammatique ELEVEN + TWO = TWELVE + ONE est attribuée par le site anagrammy.com à un certain Melvin O. Wellman (1948).

En espagnol ? Deux solutions connues :

UNO + CATORCE = CUATRO + ONCE

TRES + DOCE = DOS + TRECE

Voir là d’autres solutions anglaises (folles !) trouvées par Richard Grantham.

Et ici encore un courrier intéressant de Jean-Charles Meyrignac.

Et là un délire arabo-romain du même acabit !

Et ici de l’autoréférence dans l’irrationnel !

Retour à la page d’accueil, là.